本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
我今天在Slate上发表了一篇关于安德鲁·海克尔的书籍数学神话:以及其他STEM错觉的文章。 我之前写过关于海克尔的论点,即高中课程中应该减少数学,但现在他出了一本书,有了更多可以争论的地方。这本书充满了例子,这些例子可能来自一本关于数学文盲的书籍。正如我在Slate上写道,“我几乎希望这些是为懂数字的人准备的彩蛋,并且海克尔有一个秘密议程,即改进数学教育,直到每个人都能认识到他的论点全是胡说八道。”
在Slate的文章中,我有很多内容没有提及。例如,我漏掉了书中最为激烈的言论。在关于性别差距的一章中,海克尔指出有些人认为女性不如男性擅长数学,然后写道:“碰巧的是,关于基于性别的能力争论不会出现在其他智力领域。” 我简直无法理解这一点,所以我让艾米·波勒替我处理这件事。

真的吗?图片来源:The Frisky
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您将帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
他弄错的另一个例子也很有意思,一旦你了解了海克尔歪曲故事的方式,思考起来就很有趣了。海克尔在这里写了杰布·布什与一些学生的交流。
当他作为佛罗里达州州长访问奥兰多一所高中时,一位学生向他提出了一个问题:“”卢安娜·马克斯问道,“三-四-五三角形的角度是多少?”她想知道他是否知道,因为这样的问题出现在全州统考中,她和大约14万名高中生刚刚参加了考试。“我不知道,”她的州长承认,“一百二十五,九十,以及一百八十度剩下的度数?”
如果十几岁的杰布·布什搞砸了这样的问题,他将被拒绝获得高中毕业文凭,根据他支持和签署的一项法令。事实上,只有不到百分之三的成年人能够回答马克斯女士的问题。(这并不像看起来那么容易。)
海克尔在这里没有告诉我们一些事情。这次交流确实发生了,但是马克斯的说法不正确,她所指的佛罗里达州综合评估测试(FCAT)并没有询问关于3-4-5三角形的角度。我敢肯定,很多其他数学老师也立即看到了这个错误。
需要明确的是,学生记错了考试中的内容并向布什提问是可以理解的。我对马克斯女士没有任何意见。但海克尔应该更清楚。如果他知道足以告诉我们答案并不像看起来那么容易,他就应该知道是否应该查明这个问题是否在测试中。(事实上,它不在测试中是有记录的。)然而,他却有意省略了这一部分。如果他 включил это, 他的故事就不会支持他想要表达的观点。他只是想让那些一段时间没有接触三角学的人在面对他们不知道答案的问题时束手无策。
我是怎么知道这个问题不在测试中的?这个问题并不难——三角形是直角三角形,一些基本的三角学知识就能让你得到角度——但是老师不会要求学生回答关于那个特定三角形的这个问题。有一些特殊的三角形,它们具有易于计算的边长和角度:等边三角形、等腰直角三角形和30-60-90直角三角形。根据我的经验,这些基本上是你应该知道角度和边长的唯一三角形。
3-4-5直角三角形的角度是反正弦(4/5)、反正弦(3/5)和90度。如果有一段时间没有接触SOH CAH TOA,也没关系。角度的正弦、余弦和正切表示具有该角度的直角三角形边之间的关系。一图胜千言。标记角度 α 的正弦是对比边与斜边之比。如果这是一个 3-4-5 直角三角形,则对比边的长度为 4,斜边的长度为 5。
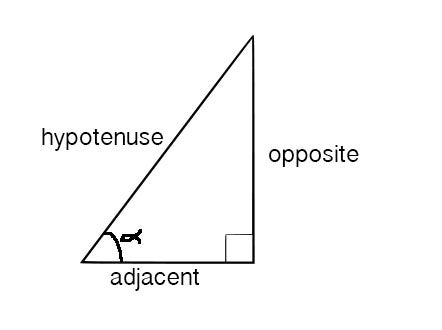
问题是,我们不认为像反正弦(4/5)这样的东西是一个数字。但反正弦(4/5)是一个完全有效的数字:它是正弦值为 4/5 的角度。(我可以听到那些迂腐的人——我可以这么说,因为我自己也是其中之一——尖叫着说有很多角度的正弦值为 4/5。我们正在寻找一个介于 0 到 90 度之间的角度,其正弦值为 4/5,所以让我们找到该范围内的那个角度并将其称为一天。)我认为我们难以这样思考这一事实说明了我们与数字的心理关系的一些有趣之处。顺便说一句,如果你看到到处都是反正弦而感到紧张,那么这个角度大约是 53 度。
十九世纪德国数学家利奥波德·克罗内克曾说过:“上帝创造了整数,其余一切都是人的工作。”我认为这很好地概括了许多人如何看待数字。尽管事实上你无法真正触摸到任何数字,但整数不知何故让我们感觉比其他数字更真实。我们以整数为中心的方式教授数学,当整数失效时,我们认为数字以小数和分数而不是以其他方式书写时更真实。有多少人知道 π 是一个数字,但当他们看到它写成 3.14159...时会感觉更舒服?
我知道我已经就一个没有出现在 FCAT 上的问题进行了相当长的题外话,但思考我们如何思考数字是很有趣的。也许所有(实)数都是实数,但有些数比其他数更实数。