本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
你如何判断你的星球是什么样子的?一种方法是发展太空计划,发射飞船,并从远处拍摄它的照片。几台相机和极少数人类离开了地球,从太空观察它,他们说它看起来像一个球体。但如果他们在撒谎呢?虽然最近的一篇论文表明,要维持一个由所有航天机构、宇航员和行星科学家组成的全球阴谋集团将是困难的,但我们不必相信他们的话。
除了发展太空计划之外,还有一种数学上巧妙、实际上不可能的方式来确定我们居住的表面类型:欧拉示性数。(这是以莱昂哈德·欧拉命名的事物列表中的众多条目之一。)早在太空计划,甚至哥伦布存在之前,人类就知道地球是球体。这不是他们弄清楚的方式。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够讲述关于塑造我们今天世界的发现和想法的有影响力的故事。
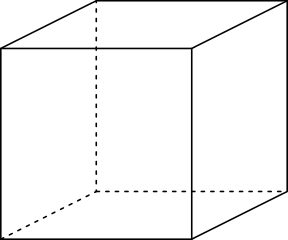
像年龄一样,欧拉示性数只是一个数字。对于像盒子、沙滩球或行星这样的二维表面,它是物体的顶点数减去边数加上面数,即V-E+F。我们将从一个简单的例子开始,一个立方体。一个立方体有8个顶点、12条边和6个面,所以总共是8-12+6=2。
球体呢?在这里,顶点和边不是凭空出现的。我们必须画出来。一种方法是在地球仪上画一条赤道和一些经线。或者,如果你没有地球仪,可以用橡皮筋绕一个葡萄柚。

我没有球形相机,所以如果你没有自己的葡萄柚,你只能相信我的话,那里有6个橡皮筋相交的顶点,12条线段和8个三角形,欧拉示性数为6-12+8=2。(这些数字恰好与立方体的数字相似。你能弄清楚为什么吗?)
在进行计算时做出选择总是很冒险的。我们对如何在葡萄柚上放橡皮筋做出了选择。如果我们以不同的方式做呢?这次我在上面放了四根橡皮筋。

现在它有10个顶点,21条边和13个面,再次得到,10-21+13=2。
事实上,无论我们如何通过绘制线条或在球体上放置橡皮筋来分解它,我们最终都会得到欧拉示性数2。* 你不必相信我的话。一个严谨的证明有点复杂,但你可以通过涂鸦轻松地让自己信服。画一个形状,并在其中画一些顶点和边。添加一个顶点和一些边。欧拉示性数会发生什么变化?擦除一条边。现在会发生什么?
欧拉示性数是一个拓扑不变量,这意味着拉伸或挤压物体不会改变它,只有撕裂或粘合才会改变它。因此,欧拉示性数可以用来确定表面的拓扑结构,但不能确定其更精细的特征。例如,立方体、球体、四面体和其他像它们这样的封闭形状都具有相同的欧拉示性数,因为它们在拓扑上是等价的。
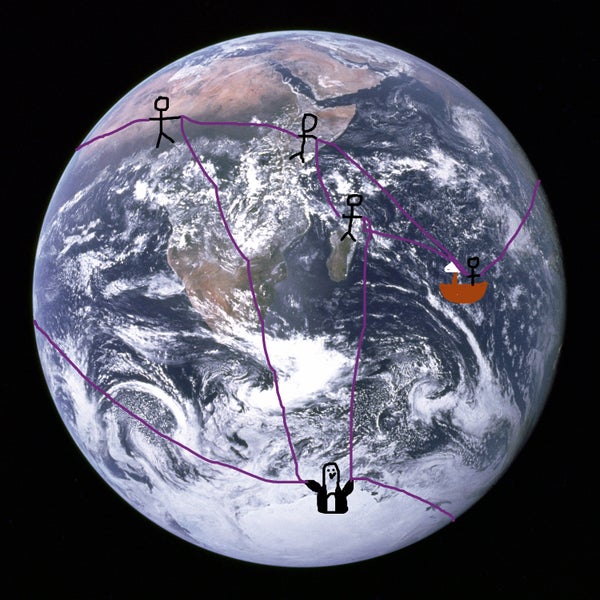
如果你是一个对科学好奇的人,没有机会进入太空亲眼看看地球,并且不想相信古代科学家或NASA的话,你可以使用欧拉示性数来确定这个星球的拓扑结构。你只需要几个朋友和很多绳子。
每个人都站在地球上的一个点上,每个人都拿着几根绳子的末端。现在你数一下有多少人,有多少段绳子,以及在这些绳段中封闭了多少个区域。然后求出欧拉示性数,V-E+F。
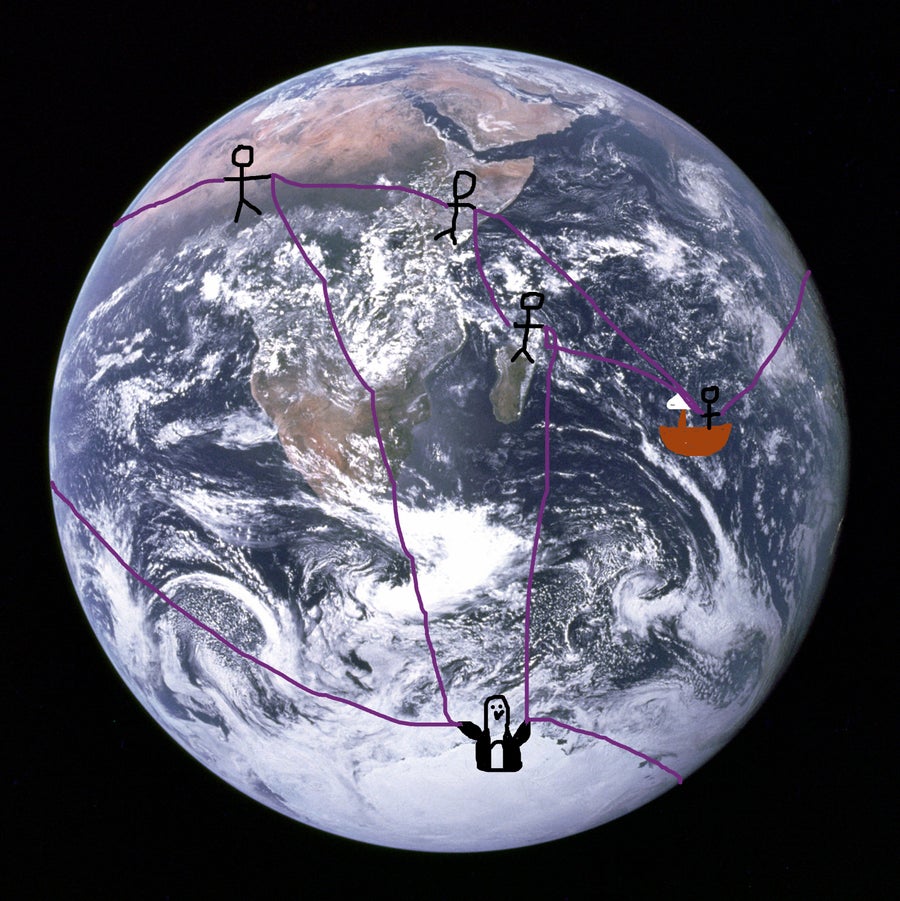
未按比例。
如果你得到2,你就完成了。拓扑学上,唯一欧拉示性数为2的表面是球体。
如果你没有得到2,你可能数错了。但假设你是在一个拓扑结构尚未确定的外星球上。该星球的其他几个方面将帮助你准确确定它是什么样的表面。
首先,这个世界是有限的,还是会永远延伸到深渊?如果世界是无限的,你就无法将其划分为几个部分并找到欧拉示性数,那么你就倒霉了。我们假设所有的世界都是有限的。

莫比乌斯带。图片:David Benbennick,通过维基共享资源。
接下来,我们要处理可定向性。莫比乌斯带是最著名的不可定向表面:如果你一直绕着它走,你最终会回到你开始的地方,但在纸的另一面。对于可定向表面,你知道有内部和外部;你永远不会倒着走回你的起点。无论你的星球是否可定向,你都可以使用欧拉示性数来确定其拓扑结构。
最后,边界。你认为有可能从世界的边缘走出去吗?如果是,有多少个独立的边缘?可能只有一个环绕外部的边缘,也可能有更多。也许你有理由相信地球的形状像一个垫圈或一个加厚的8字形。
欧拉示性数、可定向性和边界部分的数量唯一地决定了你的星球是什么样的表面。如果你得到2,你肯定在一个球体上。增加一个边界部分会使欧拉示性数减少1,所以如果你得到1,你是在一个被刺穿的球体上,它在拓扑学上等同于平面中的多边形。如果你得到0,你可能住在一个环面上,或者你可能住在一个垫圈上。列表还在继续。
一旦你知道你的星球在拓扑学上是什么样子的,你就可以开始弄清楚它的几何形状。如果你得到2,你可以尝试找出你是否住在一个球体、立方体、足球或其他奇异表面上。欧拉示性数在这里帮不了你。我建议你借鉴埃拉托色尼和其他古代天文学家的做法,开始使用阴影来确定地球在任何特定点的弯曲程度。伊桑·西格尔可以告诉你所有关于这方面的事情。
致谢:我第一次接触到使用欧拉示性数确定你的星球拓扑结构的想法是在我的朋友犹他大学数学家凯文·沃特曼的一次演讲中。B.o.B. 和尼尔·德格拉斯·泰森启发了我完成这篇文章的写作。
*为了回应评论,我要补充一点,你封闭的区域不能有孔。也就是说,它们应该像圆盘,而不是垫圈。技术术语是“单连通”。确保所有区域都是单连通的一种方法是三角剖分你的表面。