本文发表于《大众科学》的前博客网络,并反映了作者的观点,不一定反映《大众科学》的观点。
您在智慧领域中跋涉。在远处,您看到一丝闪光。难道是它吗?是的,这就是您寻找的球体!在您探索完整个表面之前,您只需要再收集几个了。
David Madore是一位法国数学家,他创造了这个以及其他在双曲平面上玩的游戏。Madore的迷宫是我发现的众多有趣工具之一,可以帮助我直观地了解双曲几何的工作原理。我推荐的其他工具包括戴娜·泰米娜的钩针编织项目,它允许您创建可触摸的双曲空间模型,以及马林·克里斯特松的双曲平铺工具。
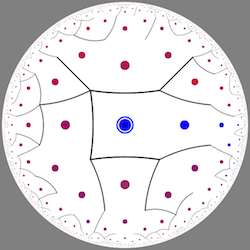
来自David Madore双曲迷宫的静帧。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
Madore有三款游戏可供选择:“玩具”版和普通版的经典迷宫,以及寻求智慧、正义和其他美德之球的探险。所有三款游戏都可以在双曲平面的庞加莱圆盘模型或贝尔特拉米-克莱因模型上进行。虽然无论您是否关心几何学,这些游戏都很有趣,但它们也融入了一些关于双曲面的复杂概念。
为了理解Madore迷宫的工作原理,我们将简要地介绍一下标准的欧几里得平面。如果我们从平面上的一个点走开,我们将离该点越来越远。(这种说法并非完全是同义反复;如果假设我们生活在一个球面上,我们最终会开始再次靠近起点。)但是有一种方法可以将无限平面变成有限空间。这与环绕式视频游戏(如小行星)的制作者使用的技术相同。
.png?w=300)
单孔环面可以剖析成正方形,双孔环面可以剖析成八边形,三孔环面可以剖析成十二边形的示意图。图片来自艾伦·哈彻的教科书《代数拓扑学》。
您从一个正方形开始,并将相对的边粘合在一起。当您走出正方形的一边时,您会从另一边进入。您可以将其表示为环面或甜甜圈,一个正方形,或平铺着无限多个全等正方形的平面。当您穿过其中一个的边时,您会走进下一个的相对边。因为这些是表示相同场景的不同方式,所以欧几里得平面上的路径等同于环面上的路径。
Madore的双曲迷宫使用了相同的想法,只不过我们使用的是双曲平面而不是欧几里得平面中的正方形。如果我们从双曲平面中的八边形开始,我们可以将边粘合在一起,得到一个有两个孔而不是一个孔的甜甜圈。如果我们从十二边形(十二条边)开始,我们可以得到一个三孔环面。具有更高亏格的曲面也可以表示为双曲平面中的多边形,而这正是Madore在他的双曲迷宫中所做的。每个迷宫都在双曲平面上进行,但Madore使用的粘合意味着它等同于在具有很多孔洞的曲面上进行游戏:玩具版有4个孔洞,完整版有8,812个孔洞。Madore在页面底部提供了关于他用于创建游戏的数学原理的更详细解释。
在您玩游戏时,您可以留意双曲空间的一些有趣方面。首先,您可以查看双曲平铺如何随着您的移动和棋盘重新居中而改变形状。您还可以通过在两种视图之间切换来探索双曲空间的庞加莱圆盘模型和贝尔特拉米-克莱因模型之间的差异。您更喜欢哪一个?
如果您更喜欢拓扑学而不是几何学,您可以检查曲面上的环。拓扑学中最重要的工具之一是同伦,即对空间中的环进行分类的过程。在平面上,任何两个环在某种程度上都是等价的:您可以毫不费力地将一个环拖到另一个环上。另一种思考方式是,从一个指定点到另一个点的任何两种行走方式在某种程度上都是相同的。然而,在环面上,并非所有环都是等价的。环绕环面孔洞的环与将您的拇指和食指穿过孔洞所得到的环是不同的。同样,在具有更多孔洞的曲面上,有很多环是不相同的。Madore在迷宫中提出的挑战之一是沿着基本不同的路径来回走动。
您还可以使用Madore的迷宫来探索双曲几何的一个决定性特征:直线彼此发散的事实。在探险游戏中,您可以在移动时留下“面包屑”。您偶尔会遇到过去的“面包屑”,但您会发现,不知不觉中,您甚至再也看不到它们了,即使这些踪迹有时非常接近。
您能想出找到所有球体的最佳策略吗?是更好地彻底搜索一个领域,还是只是不断向前走,来回穿梭于所有领域?找到所有球体需要多长时间?信不信由你,这些问题与遍历理论和动力系统中的一些主题有关,许多数学家都在研究这些主题,包括菲尔兹奖得主阿图尔·阿维拉、埃隆·林登施特劳斯和玛丽安·米尔扎哈尼。
几何学、拓扑学和动力学:对于一个易于操作的电脑游戏来说还不错。祝您探索愉快!