本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在这一集的“我最喜欢的定理”中,Kevin Knudson 和我很高兴与芝加哥大学的数学家 Amie Wilkinson 进行了交谈。您可以在这里收听,或者在 kpknudson.com 收听,该网站也有该集的文字稿。
Wilkinson 选择了 微积分基本定理 作为她最喜欢的定理。绝佳的选择!它的名字中既有“有趣”又有“基本”。微积分基本定理是连接两个看似不相关的任务的桥梁:计算曲线下的面积(积分)和求曲线的 导数(微分)。曲线 f(x) 在点 x 处的导数是曲线在该点切线的斜率,或者如果您将曲线视为对物体位置的建模,则导数是物体在给定时刻的速度。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您将帮助确保未来能够继续讲述关于发现和塑造我们当今世界的想法的有影响力的故事。
具体而言,基本定理指出,要找到曲线下的面积,即函数 f(x) 的图形,只需找到另一个函数,在下图中称为 A(x),该函数的导数为 f(x)。
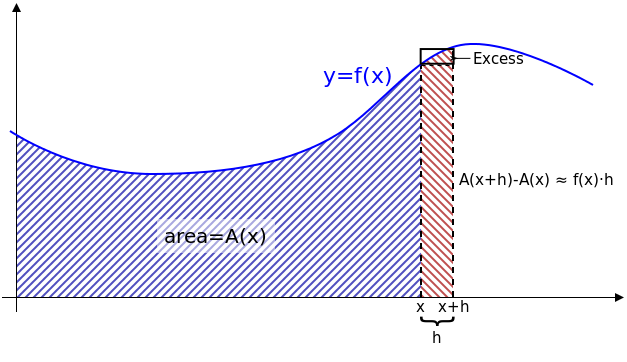
微积分基本定理的图示。红色条纹阴影区域(向下延伸到右侧)表示面积的一个小增量,一个宽度为 h 的条状区域,添加到曲线下的面积中。该图表明,添加此条状区域所产生的面积变化大约等于函数在条状区域左端点的值乘以 h。随着 h 变得越来越小,这就变成了曲线下方面积的导数是曲线高度的陈述。 来源:Kabel Wikimedia(CC BY-SA 4.0)
微积分基本定理与 中值定理 密切相关,中值定理指出,如果一个表现良好的函数在某个区间上的平均变化率为 c,那么在该区间的某个点,它的导数或瞬时变化率也必须为 c。她分享了她第一次接触中值定理的经历,即她在高中微积分课上观看的 1966 年的视频。她设法找到了它,所以你也可以观看!
平均警察定理 (1966),来自 Eric Cornwell 在 Vimeo 上。
微积分基本定理适用于一维函数,即以一个实数为输入并产生一个实数为输出的函数。但是,对于更复杂的函数,也有类似的定理。Wilkinson 谈到了 斯托克斯定理,这是一个多元微积分中的定理,类似于微积分基本定理。
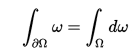
斯托克斯定理的一般形式。
我非常喜欢她描述微积分基本定理和斯托克斯定理之间联系的方式。斯托克斯定理看起来并不完全像微积分基本定理,但它们都展示了函数在对象的边界或边缘(上式中的 ∂Ω)上的值与其导数在对象内部(Ω)的值之间的这种对偶性。在基本定理的情况下,对象只是一维区间,因此“边界”只是区间的两个端点。对于斯托克斯定理,更高维的对象当然具有更高维的边界。

芒果,与微积分基本定理搭配的理想水果。 来源:Hamza Butt Flickr(CC BY 2.0)
为了与微积分基本定理搭配,Wilkinson 选择了一个成熟多汁的芒果。您需要收听这一集才能找出为什么芒果与微积分基本定理是完美的搭配。
您可以在 kpknudson.com 和 统一之根 找到有关此播客中数学家和定理的更多信息,以及其他令人愉悦的数学知识。文字稿可在此处获取。您可以在 iTunes 或任何您获取播客的地方订阅和评论该播客。我们很乐意听取听众的意见,所以请发送邮件至 myfavoritetheorem@gmail.com。Kevin Knudson 的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。请在下一次加入我们,学习另一个引人入胜的数学知识。
之前在“我最喜欢的定理”节目中
