本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
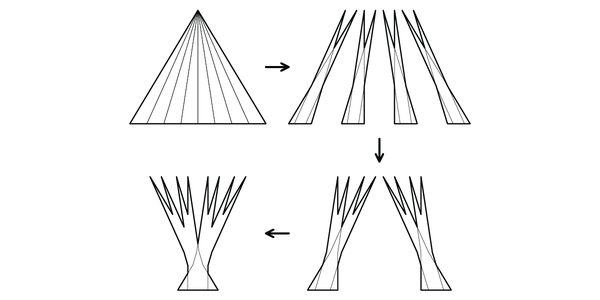
去年,我写了关于卡克亚针问题的文章,这是一个数学小问题,当我担心自己可能会陷入困境时,我会求助于它以寻求安慰。 该问题要求您在平面上旋转细针所需的最小面积。下面是一个在平面上的小区域内旋转针的例子。
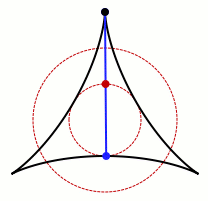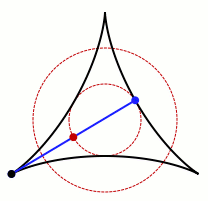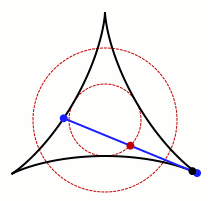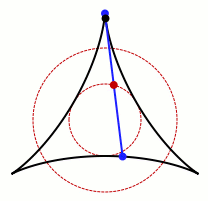
一个允许卡克亚的针旋转的集合的动画。 鸣谢:Claudio Rocchini Wikimedia (CC BY-SA 3.0)
令人惊讶的是,针可以在面积任意小的集合中旋转。这个事实是 阿布拉姆·萨莫伊洛维奇·贝西科维奇 于 1928 年证明的。他的结果基于他之前关于平面上包含指向各个方向的单位长度线段的集合的研究。 为了纪念他,这些集合被称为贝西科维奇集合。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻工作 订阅。 通过购买订阅,您正在帮助确保关于当今塑造我们世界的发现和想法的影响深远的故事的未来。
贝西科维奇集合看起来真的很酷,所以我很高兴在预印本服务器 arxiv.org 上看到一篇关于 最小贝西科维奇排列 的论文。 但是,当我开始阅读它时,我既失望又好奇。 该论文不是关于平面上的贝西科维奇集合,所以我没有看到很多漂亮的图片,但我了解了卡克亚针问题的另一个版本。 该论文研究了卡克亚针问题在不同数学环境中的转换,即有限域和有限平面世界。
我们习惯于使用像实数这样的无限数域进行算术运算,但我们也可以在有限的数字集合上定义基本运算。例如,在模算术中,也称为时钟算术,您有一个模数——比如 12——当您添加或乘以两个数字时,您查看除以模数时的余数。当您想到 10:00 五小时后是 3:00 这个事实时,该系统似乎并不那么陌生。 在报时时,我们习惯于使用模数为 12 或 24 的算术运算。(出于技术原因,对于卡克亚针问题的有限版本,模数需要是素数或素数的幂。没有卡克亚时钟!)
正如我们可以将二维平面视为所有实数对的集合一样,我们可以考虑由有限集合的成员对组成的有限平面。 例如,如果模数为 2,则该域仅包含数字 0 和 1,并且该平面为数对 {(0,0),(0,1),(1,0),(1,1)}。我们也可以查看这些数字的三元组,如果您阅读《统一之根》一段时间了,您可能会记得一个名为范诺平面的空间。 (如果不是,您可以在这里阅读相关内容。)构建范诺平面的一种方法是从零和一的三元组而不是数对开始,因此在某些方面,它是有限域上平面的三维版本。 (在此处阅读有关该描述的更多信息。)
标准二维平面中的任意两点都确定一条直线。在有限平面中也会发生同样的事情。在有限平面中,“方向”的概念不像在标准二维平面中那么清晰,但是研究过有限卡克亚针问题的人们将有限版本的贝西科维奇集合定义为平面中包含平面上每条直线上的点的集合。
为什么要将卡克亚的针移动到像有限平面这样陌生的空间呢? 除了对改变假设会发生什么情况的数学好奇心之外,这个问题是由于一个叫做卡克亚猜想的东西引起的。虽然存在面积任意小的卡克亚集合,并且存在零面积的贝西科维奇集合(使用一种称为勒贝格测度的标准面积测量方法),但该集合的维度仍然为 2。数学家已经推广了维度的概念,以涵盖维度不是整数的集合,有时我认为具有零测度是一种症状,可能表明我们正在以“错误”的维度测量其面积。 但对于卡克亚来说,情况并非如此。 平面上的贝西科维奇集合实际上是二维的。 卡克亚猜想将这个想法推广到更高的维度:在维度n 中,每个方向上都有单位长度线段的集合必须具有维度n,即使它在该维度中的测度为 0。
一些数学家开始研究有限平面版本,以此来研究微型的卡克亚猜想。 有限平面和无限平面有很多不同之处,但如果他们能够在有限空间中取得一些进展或获得一些直觉,他们可能会对更普遍的问题获得一些见解。 有关卡克亚猜想的更多信息,请参阅 Terry Tao 的这篇文章 或 Zeev Dvir 的这篇论文。
我认为有限卡克亚针问题是数学研究可以采取的曲折路径的一个很好的例子。 我们从一个有趣的问题开始,该问题是出于对一些相当有形的事物自然的好奇心而产生的,将问题推广到新的领域,发现那里太难解决,然后将问题转化为其他领域,目的是在那里获得一些进展。 激发该问题的最初想法被改变和模糊了,但数学家们希望新的、不同的问题可以帮助他们更好地理解整体情况。