2018年5月28日

我最喜欢的几个空间：阿涅西的女巫

这条不起眼、被误译的曲线到底意味着什么？

本文发表于《大众科学》的前博客网络，反映作者的观点，不一定代表《大众科学》的观点

玛丽亚·盖塔纳·阿涅西出生于1718年5月16日，所以她的三百周年纪念日是在本月早些时候。我为史密森尼杂志写了一篇文章来纪念这个日子。如果现代数学爱好者了解阿涅西，最有可能的是通过女巫曲线。这条曲线的名字来源于一个误译，由于阿涅西虔诚的宗教信仰，这个误译更显得讽刺。阿涅西在逐渐离开数学领域、投身于虔诚的慈善事业之前，写了一本开创性的微积分教科书巨著，却永远背负着女巫的名字，这可能会让人感到不满，但我们或许应该感谢这个误译，因为它让那些学过微积分的人如此了解她。

阿涅西的女巫是斯蒂格勒命名法则的一个绝佳例子，该法则指出，以人名命名的科学发现都不是以发现它的人的名字命名的。毕达哥拉斯并不是第一个知道毕达哥拉斯定理的人，帕斯卡三角形在帕斯卡活着之前几个世纪就为中国数学家所知，而阿涅西的女巫也不是由阿涅西发现的。皮埃尔·德·费马（1607-1665）研究过一般形式为（a²-x²）y=a³的曲线，而圭多·格兰迪在1703年的一篇论文中包含了这条曲线。

格兰迪最初给这条曲线命名为versiera，说他从拉丁语单词versoria改编而来，而versoria又来源于表示“转动”的词。事实上，在某些方面，2018年不仅是阿涅西的300周年诞辰，也是女巫曲线的300周年诞辰；格兰迪在1703年讨论过这条曲线，但他直到1718年才将其命名为versiera。

关于支持科学新闻

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道订阅。通过购买订阅，您将帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。

约翰·科尔森，这位将阿涅西的巨著翻译成英文的英国牧师和数学家，将 versiera 翻译为 avversiera，意思是女魔头或女巫。想听听一位脾气暴躁的数学史学家对这个误译的看法吗？（或者至少是一位数学史学家的脾气暴躁的看法？）看看 C. Truesdell 的这篇文章。“如果有人想了解我在浪费时间寻找和收集上述资料后的感受，他不妨听听K. P. E. 巴赫的 D 小调羽管键琴协奏曲。”

女巫曲线是什么？当你深入了解时，它实际上是一条不起眼的曲线，在她书中是一个有用的例子，只是许多例子中的一个。我们将看看女巫曲线在阿涅西的著作《分析机构》中的首次出现，由约翰·科尔森翻译

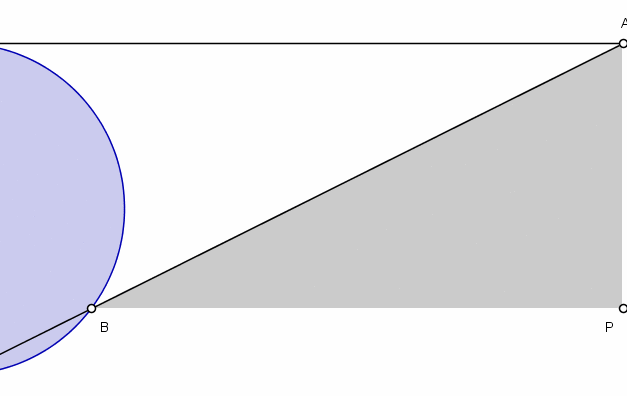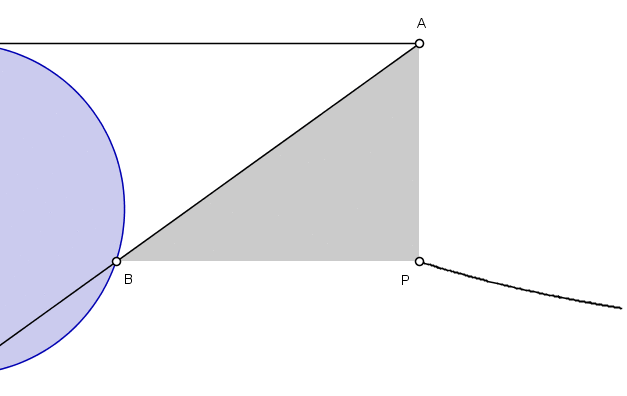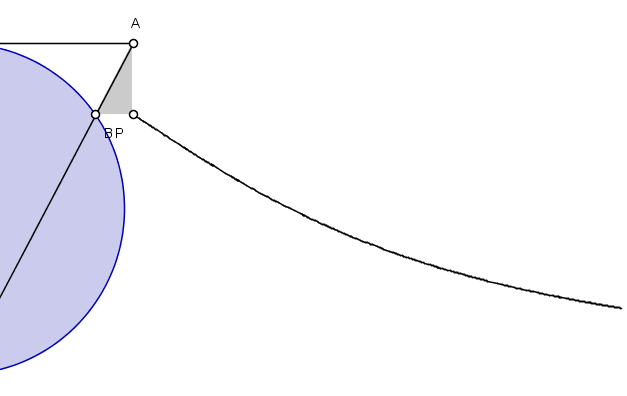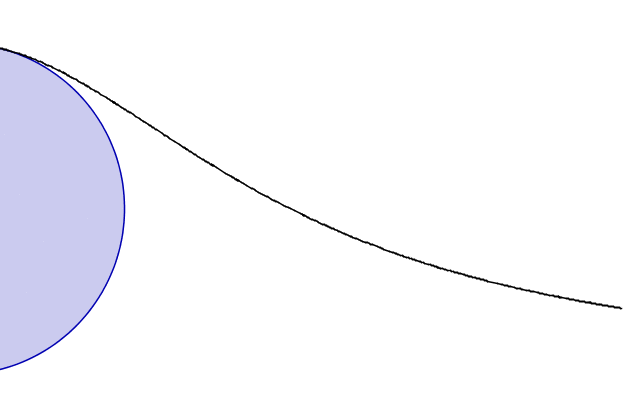
给定直径为 AC 的半圆 ADC；需要从它找到一个点 M，使得画出垂直于直径 AC 的直线 MB，该直线与圆相交于 D，则 AB.BD::AC.BM。而且，因为有无数个点可以满足这个问题，所以需要这些点的轨迹。

这个设置很需要一个图表，阿涅西提供了一个，如图表顶部所示。（据说她把一台印刷机搬进了自己的房子，以便亲自监督《分析机构》的印刷，并确保她绘制的许多图表都能正确地复制。）在这张图中更容易看清楚。

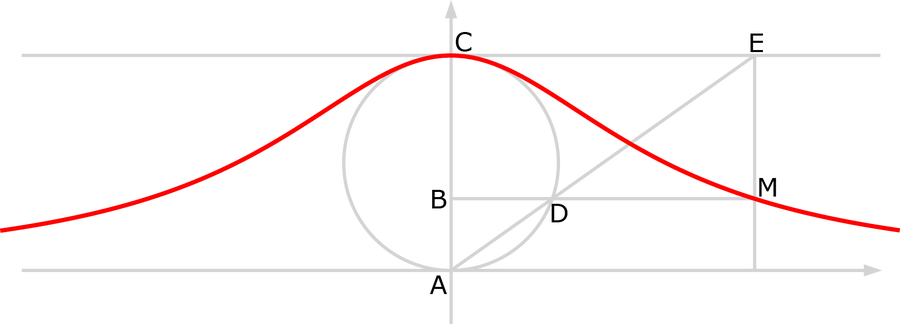
女巫曲线是红色的。图片来源：基于 zorgit *Wikimedia*(CC BY-SA 3.0)

通过一些基本的几何知识，阿涅西推导出了这条曲线的方程。在她的变量中，她得出方程 y=a(√(a-x)/(√x)。（对于今天的我们来说，她的变量是颠倒的。她用x表示垂直距离，用y表示水平距离。我们会做相反的事情。）在后面的一个问题中，她展示了一种描述这条曲线的等效方法，这导致了以下 GIF，说明了这条曲线一半的轨迹。

一个显示阿涅西的女巫曲线的图表。图片来源：Merrill *Wikimedia*

后来她还找到了这条曲线的拐点。（这条曲线中间部分像帽子一样向下弯曲，两端像碗一样向上弯曲。帽子和碗之间过渡的点是拐点。）

关于女巫曲线，没有太多其他要说的了。它是一条不错的曲线，但没什么特别之处。许多微积分学生都用它来探索参数方程，它与一种被称为柯西分布的病态概率分布有关。如果科尔森在翻译的时候没有发挥一点想象力，我们可能没有太多理由在阿涅西书中数十个例子中特别记住它。这表明良好的品牌塑造对于一条渴望聚光灯的勇敢曲线来说是多么重要。

想更多地了解女巫曲线吗？感谢互联网的魔力，您可以免费阅读阿涅西书籍中的关于女巫曲线的内容，无论是意大利语（第 1 卷，第 2 卷）还是科尔森的英语翻译。La versiera 出现在意大利语版本的第 382 页、392 页和 561 页。该图表是第一卷后面的图 135。女巫曲线出现在英文版第 1 卷的第 222 页和 229 页以及第 2 卷的第 79 页。您还可以在在线图形计算器 Desmos 上探索这条曲线。