2016年4月18日

我最喜欢的一些空间：沃利斯筛

这个奇怪的分形物体让你从正方形中“挤出 π”

本文发表于《大众科学》的前博客网络，反映了作者的观点，不一定反映《大众科学》的观点

几周前我从没听说过沃利斯筛，但它很快在我的最喜爱空间列表中占据了一席之地。我从 Matt Parker 的这个视频中了解到了这个空间。

Parker 从未指名沃利斯筛，但它就在那里。沃利斯筛是一个分形物体，最容易通过从谢尔宾斯基地毯开始解释。谢尔宾斯基地毯是一个二维分形，有点类似于我去年写过的康托集。要制作一个，取一个边长为 1 的正方形，将其分成 9 个小正方形，然后移除中间的正方形。然后将每个剩余的正方形分成 9 个小正方形，并移除中间的正方形，依此类推。

关于支持科学新闻

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道订阅。通过购买订阅，您将帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。

谢尔宾斯基地毯构造的六个阶段。图片：KarocksOrkav, via Wikimedia Commons。CC BY-SA 3.0。

沃利斯筛的起始方式与谢尔宾斯基地毯相同：取一个边长为 1 的正方形，并移除中间的九分之一。然后事情变得有趣起来。我们没有移除所有剩余正方形的中间九分之一，而是将每个正方形分成 5×5 的网格而不是 3×3，并移除每个正方形的中间正方形，最终得到总面积的 1/25。在下一步中，我们将所有剩余的正方形分成 7×7 的网格，并从每个正方形中移除中间正方形，即剩余面积的 1/49。

与谢尔宾斯基地毯不同，我们总是移除 1/9，而沃利斯筛每次移除剩余集合的比例较小。谢尔宾斯基地毯最终的面积为零，就像康托集一样，但沃利斯筛具有正面积，就像一个被稍微“增肥”的肥康托集。

不过，在开始进行一些计算之前，我应该指出，关于沃利斯筛到底是什么，存在一些歧义。我描述的图形面积为 π/4，与半径为 1 的四分之一圆的面积相同。有些人觉得将四个这样的图形拼在一起得到面积为 π，或一个完整的单位圆，并称该图形为沃利斯筛更令人满意。在这篇文章中，我将坚持我之前的定义。

无论如何，沃利斯筛的面积与圆的面积密切相关。为什么？这一切都归结于沃利斯乘积。英国数学家约翰·沃利斯在 1655 年推导出了这个奇特的公式

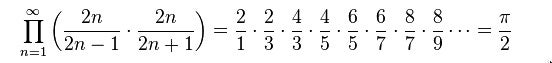
乍一看，这个乘积似乎与沃利斯筛没有太大关系，但让我们重写一下。我们将忽略开头的 2/1，并将剩余的项配对。我们得到 2/3×4/3=8/9，4/5×6/5=24/25，依此类推。当我们以这种方式看待乘积时，沃利斯筛就显现出来了。

在创建筛子的第一步中，当我们移除正方形的中间九分之一时，我们剩下的面积为 8/9。然后，当我们移除剩余正方形的中间二十五分之一时，我们剩下剩余面积的 24/25，总面积为 8/9×24/25。然后我们移除每个剩余正方形的中间 1/49，剩下剩余面积的 48/49，即原始正方形的 8/9×24/25×48/49。总共（并考虑到我们之前忽略的 2），我们发现沃利斯筛的面积为 π/4，与半径与筛子边长相同的四分之一圆的面积相同。

我想知道是否有一种简单的方法可以看出沃利斯筛与圆如此密切相关。也就是说，如果你挤出所有的空白空间，你会得到一个四分之一圆吗？我设想将所有东西都推向左下角。

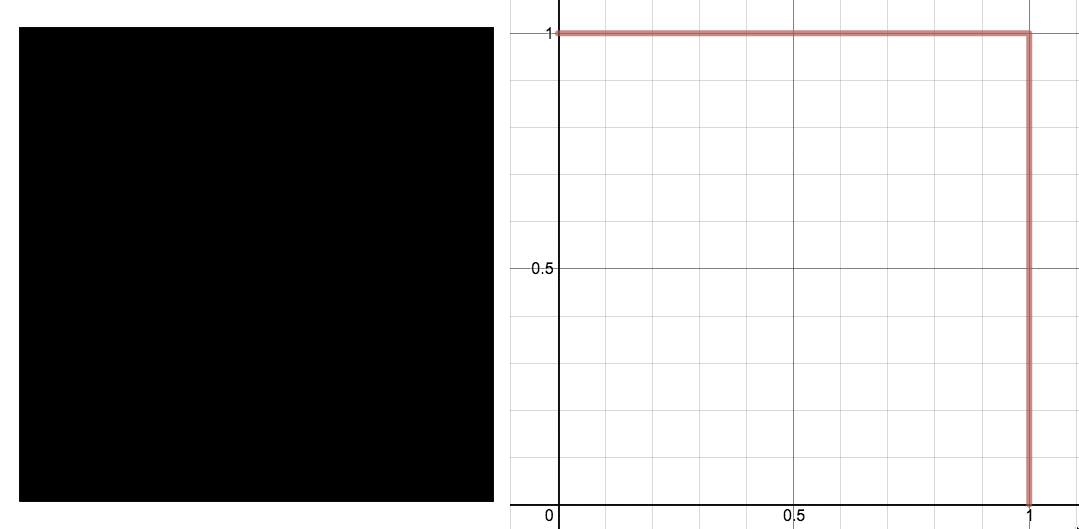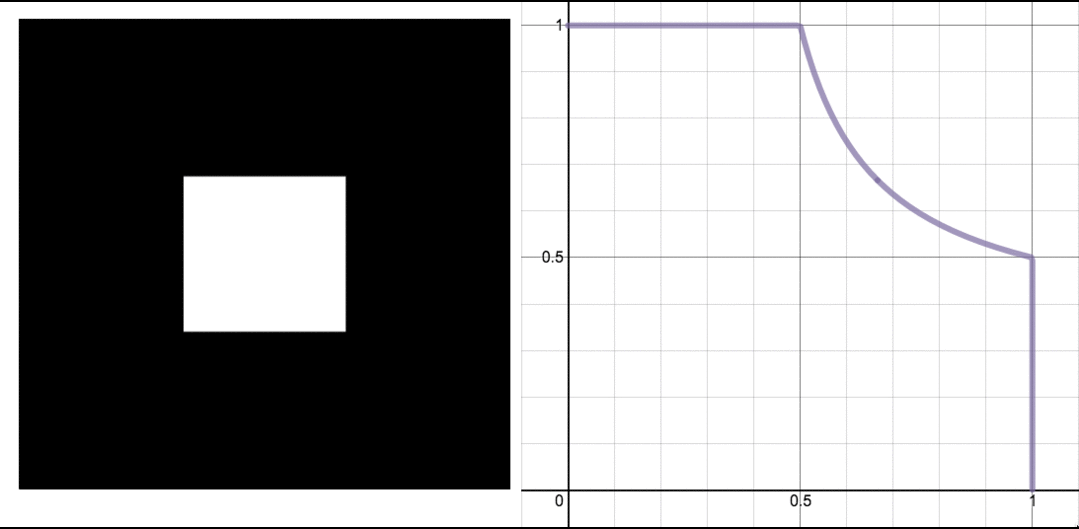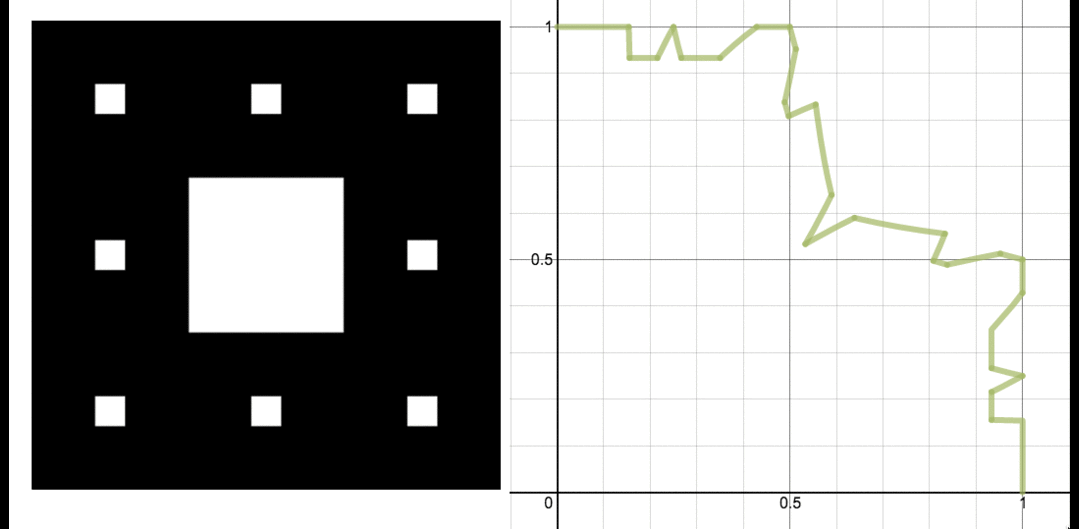
一个动画，展示了沃利斯筛的三个阶段，以及如果我们把所有东西都挤到正方形的左下角会发生什么的可视化效果。图片：Evelyn Lamb，在 Desmos 的协助下制作。

可惜的是，我对简单解释的希望立刻破灭了：第一步，移除中间的九分之一，在某些地方移除了足够的长度，以至于最终不可能得到圆形的东西。

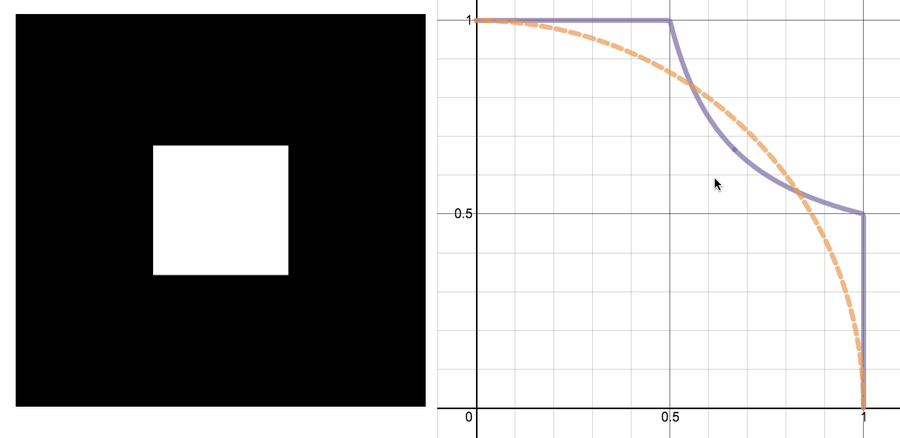
左图：移除了中间九分之一的正方形。右图：图表显示了将正方形向下和向左挤压的结果（实线紫色曲线）与圆形楔形（虚线橙色曲线）的对比。图片：Evelyn Lamb。

关于这个有趣的小形状，我剩下的问题多于答案。有没有一种简单的方法可以看出它的面积应该与四分之一圆的面积相同？如果我把它完全压扁，它会是什么样子？边界会是有限长度吗，还是最终我会得到更像科赫曲线的东西？我们甚至还没有讨论到三维版本！正如 Parker 在帖子顶部的视频中指出的那样，在三维空间中类似的构造会得到一个体积与单位球体相同的物体！我们可以在更高的维度中做同样的事情吗？

我希望沃利斯筛和相关问题像 nerd snipe 你一样 nerd snipe 我。如果您渴望了解更多信息，Ed Pegg 的文章“从门格海绵中挤出 pi”和 Mike Lawler 关于与孩子们分享沃利斯筛的博文是您自己探索的良好起点。