本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
啊,不起眼的圆环:初学拓扑学家的朋友,也是理论与实践之间差距的体现。圆环有许多生命,并在数学的各个领域中出现。
首先,它具有拓扑生命。拓扑学并不关心你的确切形状,它只关心大规模的特征。具体来说,它关心的是物体在拉伸或挤压时保持不变的方面,只要没有撕裂。在拓扑世界中,圆环是一个二维空间,或曲面,带有一个孔。(更专业一点说,它是一个可定向的亏格为一的曲面。)拓扑学家渴望将自己与更具吸引力的糕点主题联系起来,将圆环描述为甜甜圈,尽管要令人讨厌地精确地说,它只是糖霜。(甜甜圈的面包是一个三维空间,称为实心圆环。)
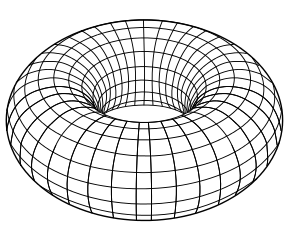
图片来源:公共领域,来自维基共享资源。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的思想的具有影响力的故事。
通常,我们将圆环表示为一个丰满的甜甜圈,但拓扑学家也偏爱一种更抽象的方式来描绘它。在这张图中,我们将其绘制为一个带有少量标记(称为标识)的矩形。
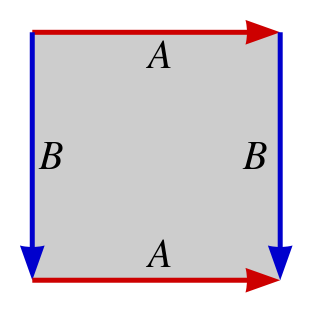
顶部标记为“A”的箭头与底部标记为“A”的箭头粘合在一起,左侧标记为“B”的箭头与右侧标记为“B”的箭头粘合在一起。图片来源:公共领域,来自维基共享资源。
就像经典的电脑游戏《小行星》一样,当您从矩形的顶部向上移动时,您会在底部重新出现,而穿过右侧会导致您在左侧重新出现。虽然这张图不如甜甜圈那么诱人,但它仍然向我们展示了圆环的所有重要拓扑性质。
平坦矩形的图片也很好地过渡到圆环的另一个生命,即它作为几何物体的生命。与拓扑学相反,几何学确实关心确切的形状和距离。丰满的圆环和纤细的圆环在拓扑学上是相同的,但在几何学上是不同的。
几何学家关心圆环的矩形图片,因为它是一个有限的曲面,从根本上来说是平坦的,就像无限平面一样。如果您曾经意识到格陵兰岛的面积是非洲的7%,而不是几乎相同的大小,那么您就暗中意识到球体无法以保留距离的方式展平到平面上。那是因为它是正弯曲的,而平面是平坦的。还有负弯曲的曲面,它们也不能在没有一些变形的情况下展平到平面上。
圆环的矩形图片证明了圆环是平坦的。那么,如果能够将圆环视为三维空间中的平坦曲面,而不是仅仅在纸上绘制并使用我们的想象力,那将是非常好的。我们可以尝试通过在矩形图片中执行标识来实现这一点。我们从一个矩形开始。
.JPG?w=300)
第一个粘合过程将我们从平坦的纸片变成圆柱体。
.JPG?w=300)
第二个粘合过程将圆柱体的两端连接在一起。
.JPG?w=300)
问题就在这里。组装这个圆环的过程并不像计划的那么顺利。这是一个理论与实践的皱巴巴的碰撞。
.JPG?w=300)
#sadtorusselfie(#悲伤圆环自拍)
当任何数学对象进入现实世界时,都不是完美的。我们画的任何圆都不是完全理想的,而且我们画它的表面也不是真正的二维物体。但是通过一些小心和一个好的圆规,我们可以制作一个足够接近我们目的的圆。另一方面,圆环有点像一场噩梦。
那么,我们能否希望将圆环放置在三维空间中,使其距离不会失真呢?

基于公共领域图像,来自维基共享资源。
我们能做到!但这并不像你可能希望的那么简单。
一种选择是放弃曲面的光滑性。在平面中,矩形没有任何褶皱,但如果我们加入一些褶皱,我们就可以让事情奏效。有很多方法可以实现这一点。几年前我做了一个。
.jpg?w=300)
数学 3D 打印奇才 亨利·塞格曼 有一个很好的例子,其中脊是铰接的。
如果我想要更多呢?如果我想消除那些刺耳的、难看的褶皱呢?好吧,我们也可以做到!但这变得有点复杂。在 2012 年,文森特·博雷利、赛义德·贾布拉内、弗朗西斯·拉扎勒斯、鲍里斯·蒂贝尔和达米安·罗默发表了第一批在三维空间中实现平坦圆环而没有任何锯齿状拐角的图片。他们写道:“这些图像揭示了一个意想不到的物体,介于分形和普通曲面之间:一个光滑的分形。”换句话说,他们将分形的无限性质与平滑过程相结合,以避免尖锐的脊。

图片来源:博雷利、贾布拉内、拉扎勒斯、蒂贝尔、罗默,在他们的PNAS 论文中。
最后,“平坦”圆环看起来一点也不平坦,但它设法满足了字面意义上的要求。所有距离都与平面上矩形上的距离完全相同。有关这种光滑分形圆环的更多信息,请参阅 Lê Nguyên Hoang 的详细文章、这篇文章和 Aperiodical 的 Christian Lawson-Perfect 的 视频,或关于该主题的 Numberphile 视频。
圆环还有许多其他生命:在拓扑学中,它是乘积空间的第一个例子之一,也是使用塞弗特-范坎彭定理的一个有用的首次尝试。在动力学中,它是学生遇到的第一个平移曲面之一,并在其中玩台球。在我的领域,泰希米勒理论中,它是唯一足够简单的曲面之一,你可以真正理解和计算它的泰希米勒空间。一般来说,似乎圆环通常是在遇到新想法时胜过千言万语的例子。在感恩节的精神下,让我们花一点时间感谢圆环,感谢它在我们遇到二维几何或拓扑时始终是一个有用的例子。(毕竟,在可定向的亏格为一的糕点上研究数学总是更棒。)
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 有两间房子的房子 法诺平面 三圆环 莫比乌斯带 长线 空间填充曲线