本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
每年这个时候我都会想到谢尔宾斯基三角形。
我敢说你看完那个视频之后,吃糖果玉米时不会唱“糖果玉米上校,糖果玉米上校”。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
谢尔宾斯基三角形,像许多分形一样,可以“向上”或“向下”构建。“向下”构建它,从一个实心三角形开始,然后移除中间四分之一,移除每个剩余三角形的中间四分之一,依此类推。无限次迭代后得到的对象就是谢尔宾斯基三角形。
要“向上”构建它,建议使用糖果玉米:制作一个小糖果玉米三角形,然后制作一个三角形的三角形,然后制作一个由这些更大的三角形组成的三角形。每次迭代它都会变得更大更复杂。说谢尔宾斯基三角形是你无限重复这个过程得到的最终结果没有太大意义,因为那样它会蔓延到各处,但你可以想象在每个阶段你拍一张照片并将其缩小,使其占据与之前相同的空间。
除了构建谢尔宾斯基三角形的两种直接方法外,还有许多其他过程似乎都神奇地收敛到谢尔宾斯基三角形。你可以玩一种叫做“混沌游戏”的游戏,并观看随机起点如何根据一些简单的规则转换为谢尔宾斯基三角形。你可以在帕斯卡三角形中为所有奇数着色,帕斯卡三角形是由包括中国和印度在内的几种不同文化发现的,早于帕斯卡出生几个世纪。你可以在一个大网格上绘制一个黑色方块,然后继续遵循称为规则 90 的元胞自动机。
但我想考虑另一种方法,称为谢尔宾斯基的箭头曲线。要制作这个漂亮的形状,你从一条锯齿线开始。在每个步骤中,你根据一些规则,用另一条锯齿线替换每个直线段,你可以在此图中看到这些规则的出现。
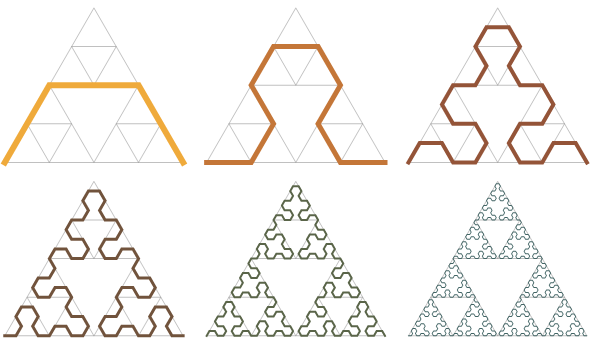
经过几次迭代后,谢尔宾斯基三角形在这个曲线中显现出来。 鸣谢:Robert Dickau Wikimedia (CC BY-SA 3.0)
我喜欢箭头曲线,因为它表明,不仅可以通过在空间的移除三角形版本中削减二维形状来接近谢尔宾斯基三角形,而且还可以通过构建一维对象来创建它。这在直觉上是有道理的:谢尔宾斯基三角形既不是完全一维的,也不是完全二维的。它实际上更像是 1.585 维的。(有关分数维度的含义的更多信息,请查看我关于另一个具有分数维度的对象 门格海绵 的帖子。)如果你可以通过稀释二维物体或增肥一维物体来制作相同的物体,那么在某种意义上,它的维度介于这两个数字之间是有道理的。
瓦ц瓦夫·谢尔宾斯基的名字出现在一些非常好的数学对象上。除了这个美妙的三角形之外,还有一个类似形状叫做谢尔宾斯基四面体,它存在于三维空间中。然后是谢尔宾斯基地毯,这是我几个月前写过的门格海绵的二维版本。最后,还有一个空间简称为谢尔宾斯基空间,它只有两个点。数学研究生 Tai-Danae Bradley 最近在她的博客 Math3ma 上写了一篇关于为什么这两个微不足道的点很有趣的帖子。
那些其他以谢尔宾斯基命名的空间都非常值得尊敬,但三角形是最有万圣节味道的。
.png?w=283)
鸣谢:Evelyn Lamb
阅读更多关于我最喜欢的空间
康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的线 有两间房子的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫环的连通和 博罗梅安环
