本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点。
当你看着铁轨时,它们的平行边缘似乎在你凝视远方时会收敛。但你知道平行线永远保持等距。或者至少到铁轨的尽头。被称为射影平面的空间是我们看到平行线似乎收敛时的光学效应的数学模型。
我之前在这里写过一篇关于射影平面的文章。它被称为法诺平面。它是一个有限射影平面,由七个点和七条线组成。
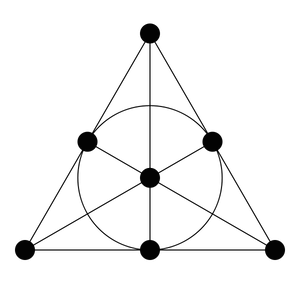
法诺平面。七个点是七个大的黑色圆圈。七条线是连接每 3 个点的六条线段,以及中间的圆圈。图片来源:维基共享资源
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
它具有以下属性
每对点恰好由一条线连接。
每对线恰好在一个点相交。
存在四个点,使得没有一条线包含其中多于两个点。
任何满足这些规则的东西都是一个射影平面,但当数学家提到这个射影平面时,他们通常指的是更恰当地称为实射影平面的空间,或 RP2。这可以用几种等效的方式定义,查看不同的定义可以帮助我们更好地理解这个空间。
射影平面对我来说是最难想象的“基本”数学对象之一。我称之为基本,即使它不是你遇到的第一个数学对象之一,因为它是其他曲面的构建块之一,正如Emille Davie Lawrence 在我们为“我最喜欢的定理”播客采访她时提到的那样。尽管射影平面具有难度和抽象性,但它有着具体的起源。那些似乎在远处消失的铁轨——你如何绘制它们?当文艺复兴时期的艺术家开始使用消失点(画布上或画布外的平行线似乎会收敛的点)绘制透视场景时,射影几何的种子就被种下了。
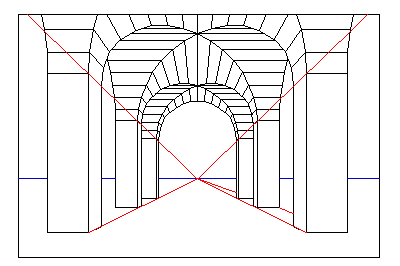
RP2 的描述最接近艺术透视,这正是我所认为的约定俗成的数学的一个例子。我们声明它,所以它就是这样。从实数二维平面开始。现在,对于平面上的每组平行线,例如所有垂直线或所有水平线,附加一个“无穷远”的点,该点连接到所有线。现在这些线相交了。为了满足每对点恰好由一条线连接的要求,我们决定将所有“无穷远点”的集合称为“无穷远线”。在每种情况下都很难弄清楚,但是这些规则使普通的欧几里得平面变成了射影平面。我发现它很难可视化,即使它是最接近消失点概念的。那些无穷远点太远了。我看不见它们。
对我来说,更容易理解 RP2 的描述是穿过 3 维空间中单个点的所有线的集合。因此,每条线都是这个空间中的一个“点”。思考这种描述的另一种方式是想象在某个地方画一个穿过它的球体。现在我们可以只考虑这个二维球体上的点,其中对径点或相反的点被识别出来,因为对于每对对径点,同一条线穿过它们。换句话说,北极和南极被认为是同一点,球体上彼此相对的所有其他点对也是如此。(想知道地球上与你相对的位置在哪里吗?这里有一张地图。剧透:很可能是在水里。)
为了可视化射影平面的这种描述,你可以想象沿着赤道切割地球仪的表面,并将顶部和底部恰到好处地粘合在一起。你想粘合,比如说,被赤道切割的厄瓜多尔北部,不是粘合到厄瓜多尔南部,而是粘合到印度尼西亚某个与它完全对径的位置。困难的部分,至少如果你想用真实的地球仪执行这种全局重排,是赤道本身。它需要自身缠绕,以便厄瓜多尔在马来西亚的上方。你可能已经猜到了,在现实世界中不可能完美地做到这一点,但是作为数学家,我们可以想象我们可以做到。
不难看出,射影平面的这种描述满足上述三个要求。首先,球体本身就很接近。在那里,任意两点之间至少有一条线,任意两条线至少相交一次。问题是对径点。北极和南极之间有很多线连接,即经线。射影平面通过声明北极和南极实际上是同一点来解决这个问题。一般来说,任何两个大圆(看起来像地球仪上的赤道或经线的线)都在对径点相交,所以一旦我们将对径点视为相同,我们就清楚了。
思考射影平面的另一种方式是将其视为莫比乌斯带,并在其上粘贴一个圆盘。Ronnie Brown 的这个动画(感谢 Tai-Danae Bradley 让我意识到这一点)展示了如何从空间的奇怪半球描述变为带有圆盘描述的莫比乌斯带。(更多信息请点击此处。)
去年,我在一次会议上遇到了石溪大学的数学家 Moira Chas,她向我展示了这个精巧的射影平面织物模型。(这个想法来自多年前石溪大学的研究生。)她在织物莫比乌斯带的侧面和一块织物圆盘上缝了一个拉链。然后你可以通过将两块织物拉在一起组装射影平面。

Moira Chas 制作了这个织物模型,展示了如何从莫比乌斯带和圆盘组装射影平面。图片来源:Moira Chas 和 Clara Sullivan
你也可以从莫比乌斯带得到射影平面,而无需圆盘。你只需要以正确的方式将莫比乌斯带边界的一半粘合到另一半边界。这在图表中看起来比在现实生活中容易得多。除非你比我更能忍受挫折,否则不要尝试用实物来做。

要制作莫比乌斯带,请扭曲正方形,以便你可以将标有 A 的边粘合在一起,箭头对齐。然后要将莫比乌斯带变成射影平面,对标有 B 的边做同样的事情。祝你好运!图片来源:维基共享资源
射影平面不能完全正确地放入 3 维空间,当你尝试让织物模型表现良好时,你会看到这一点。莫比乌斯带做得很好,但是当你尝试粘合(或拉上拉链)圆盘时,它必须在某处自相交。有几种不同的方法可以将其放入 3 维空间。一个特别可爱的例子被称为 博伊曲面,以德国数学家 Werner Boy 的名字命名。它是曲面投影到 3 维空间中最平滑的方式之一。它没有任何曲面被挤压的点,但它确实广泛地自相交。

博伊曲面在空间中旋转。图片来源:A13ean 维基共享资源 (CC BY-SA 4.0)
很难相信所有这些图片都显示了同一个曲面。每张图片都突出了空间的不同特征。我不太明白当这些描述消失在远处时,它们如何收敛到同一个空间,但我知道它们一定会的。
有关射影平面的更多信息
克里斯·兰比-汉森撰写的《射影平面的另一种介绍》 本诺·阿特曼撰写的《射影平面的图片》(pdf) 泰-达娜·布拉德利撰写的《实射影平面的基本群》
阅读更多关于我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 带有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛子 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫链环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔子 庞加莱同调球 科瓦列夫斯卡娅陀螺 一个 6 孔环面