本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
我教学生涯中最美好的时刻之一,是一位学生带着一个伪球面走进我的教室的那一天。那是一个美丽的伪球面,是用木头在车床上手工制作的。(他在班级博客上写了关于制作它的文章。)我们一直在关于非欧几何发展的数学史单元中讨论伪球面,但我从未梦想过学生会用一个沉重的模型取代我在黑板上糟糕的草图,更不用说像这个一样漂亮的模型了。
伪球面是一个具有恒定负曲率的表面。曲率的严格定义有点棘手,但理解它的含义并不太难。它是衡量表面的一部分偏离平坦程度的指标。曲率可以是正的、负的或零。如果您想象坐在表面上,那么最容易理解这些含义。如果您坐在一个大球上,球的表面会向各个方向弯曲远离您。那是正曲率。如果您坐在马鞍上,马鞍会沿着您的腿垂下的方向弯曲远离您,并朝另一个方向弯曲靠近您。那是负曲率。具有零曲率的表面是平坦的。
这三种类型的曲率对应于二维几何的三种基本类型:正曲率对应于球面几何或椭圆几何。那是我们在地球上远距离导航时所做的几何类型。零曲率是熟悉的欧几里得几何,负曲率是双曲几何。虽然一些数学家几次接近发现它,但直到 19 世纪 30 年代,尼古拉·罗巴切夫斯基和雅诺什·博雅伊发现它与欧几里得几何一样一致,双曲几何这个最后的选择才被认为是可行的系统。
支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
18 世纪的瑞士数学家约翰·海因里希·朗伯在博雅伊和罗巴切夫斯基之前几十年,几乎就要发现(或发明)双曲几何了。在我两年前写的一篇文章中,我分享了他一篇论文中的以下引言。他提到的第二和第三个假设基本上相当于臭名昭著的欧几里得平行公设是否在球面方向被违反,这会产生内角和大于 180 度的三角形,或者在双曲方向被违反,这会产生内角和小于 180 度的三角形。
回到第三个假设。正如我们刚刚看到的,在这个假设下,每个三角形的三个角的和都小于 180 度,或两个直角。但是,高达 180 度的差值会像三角形的面积一样增加……
我只想补充以下评论。在第二个假设下,除了在它之下,每个三角形的角和都大于 180 度之外,完全类似的定理也成立。超出的部分始终与三角形的面积成正比。
我认为值得注意的是,如果我们将平面三角形改为球面三角形,第二个假设就成立了,因为它的角和大于 180 度,超出的部分也与三角形的面积成正比……。
由此我几乎可以得出结论,第三个假设在某个虚构的球体上成立。
伪球面就是那个虚构的球体。
嗯,有点像。朗伯指的是球面三角形的面积公式,该公式指出,如果球体的半径是某个数字R,并且该球体上三角形的角是a、b和c,则该三角形的面积为(a+b+c-π)R2。朗伯发现,如果您假设他所谓的“第三个假设”(数学家现在会认为是平行公设的双曲版本),则角度为a、b和c的三角形的面积将是(π-a-b-c)R2,其中R是一个常数。因此,他注意到,如果我们将一个虚数代入球体面积公式,用iR替换R,其中i2=-1,我们将完全得到他假设第三个假设而发现的三角形面积公式。
伪球面不是由等价于用虚数替换球体半径的方程定义的。但我仍然相信朗伯的评论预示了这个可爱的图形。伪球面的名称来自于它与球体共享的一个重要特征:它具有恒定的曲率。还有其他物体,如鸡蛋,在各处都具有正曲率,但球体是唯一具有恒定正曲率的物体。从曲率的角度来看,球体的每个点看起来都相同。同样,伪球面,除了中间的尖锐尖端外,都具有恒定的负曲率。这使其成为双曲几何的天然栖息地,就像球体是球面几何的天然栖息地一样。与正曲率的情况不同,伪球面在这种性质上并非独一无二。有许多许多具有恒定负曲率的表面,它们在其他方面彼此不等价。
要制作伪球面,您需要取曳物线,这是平面上的一条曲线,由卢浮宫建筑师克劳德·佩罗(不幸的是,他认为不适合在卢浮宫中使用它)于 1670 年首次研究,并将其绕轴旋转。
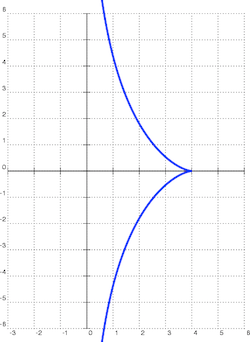
曳物线。 来源:佩德罗·桑切斯 (CC BY-SA 3.0)
1868 年,意大利数学家欧金尼奥·贝尔特拉米发表了一篇关于如何使用伪球面来实现罗巴切夫斯基几十年前撰写的非欧几何的论文。

通过围绕轴旋转曳物线制成的伪球面。 来源:克劳迪奥·罗基尼 (CC BY-SA 3.0)
在这篇文章的顶部,我通过指出“Ceci n’est pas une pseudosphère.”,对伪球面进行了马格里特式的处理。这个伪球面的欺骗性不是马格里特著名的非烟斗的欺骗性。不仅仅是因为这个伪球面是屏幕上的像素,而不是真实的、三维的物体。不,这个木制模型,尽管它很华丽,也不是伪球面。除了在现实世界中使用真实材料所引入的任何小错误之外,曳物线是一条无限曲线,因此伪球面在两个方向上都永远延伸。数学对象与现实世界的对象不同,我可以在我文章中包含的任何数学对象的图片上附加此免责声明。但我认为它看起来特别适合搭配这个特定的数学模型。
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 有两间房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼
