本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
有五个柏拉图立体。这些最对称的立体是正四面体、立方体、正八面体、正十二面体和正二十面体,是仅有的凸(没有指向内部;更像球而不是星星)立体,其面都是全等的正多边形。正四面体、正八面体和正二十面体由等边三角形构成(每个顶点分别有三个、四个或五个三角形),立方体由正方形构成,正十二面体由正五边形构成。
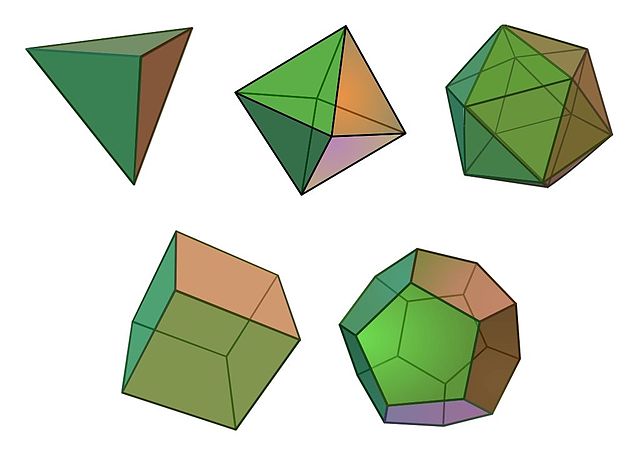
柏拉图立体。顶行:正四面体、正八面体、正二十面体。底行:立方体、正十二面体。 鸣谢: Максим Пе Wikimedia (CC BY-SA 4.0)
柏拉图立体很可爱,但数量有限。一旦你找到了它们,你的大脑自然会开始询问还有哪些仍然相当规则和对称的立体。你可能会想到下一个棱柱和反棱柱,但老实说,它们可能有点乏味。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的有影响力的故事的未来。
阿基米德立体更加有趣。在这里,面仍然是正多边形——等边三角形、正方形、正五边形等等——但它们会将两种或多种形状混合在一起。为了获得最大的规则性(这是什么,酸奶广告?),我们仍然要求所有顶点看起来都相同。如果一个顶点周围的形状是三角形-五边形-三角形-五边形交替,那么它们都是这样。
如果你坐下来,拿着一堆多边形,这些规则,以及大量的耐心,你会发现 14 种符合条件的立体。(如果你偶然发现任何近似值,你甚至可能会发现一些额外的立体。)但阿基米德最初的清单上只有 13 种,数学家们在很大程度上同意他的清单,并使用阿基米德立体的定义,其中仅包括这 13 种。
不属于这个范畴的立体被称为伸长型正方形双圆顶或伪菱面立方八面体(立体的名称非常复杂)。
伪菱面立方八面体,我将在下文中称之为 ψρ(“psi-rho”),有 24 个顶点,每个顶点周围有三个正方形和一个等边三角形。它是菱面立方八面体的近亲,菱面立方八面体也是阿基米德立体,也有 24 个顶点,每个顶点周围有三个正方形和一个等边三角形。
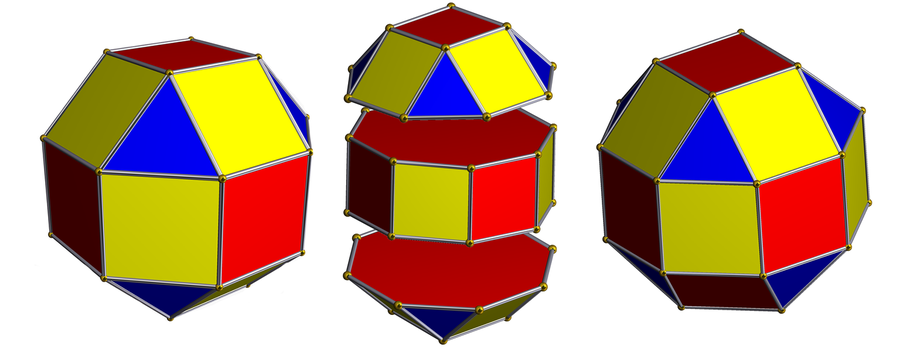
左图:菱面立方八面体。中图:解剖图显示两个圆顶和一个穿过中间的正方形带。右图:伪菱面立方八面体。你可以看到如何通过将其中一个圆顶旋转八分之一圈,将菱面立方八面体变成伪菱面立方八面体。鸣谢: Robert Webb's Great Stella software Wikimedia. http://www.software3d.com
要从菱面立方八面体获得 ψρ,你可以分离底部部分(恰好是一个称为正方形圆顶的形状),并将其旋转整整八分之一圈。
菱面立方八面体是阿基米德立体,而 ψρ 则不是。两者都是由正多边形制成的凸立体,并且在两者中,每个顶点都由三个正方形和一个三角形包围。但菱面立方八面体具有 ψρ 不具备的属性。你可以选择菱面立方八面体上的任意两个顶点,并执行对象的旋转,将第一个顶点移动到第二个顶点。这比立方体或正四面体更难可视化,但原理相同。如果你用 ψρ 尝试同样的操作,它就不会完全起作用。起初不容易看出来,但对我帮助最大的描述是将上图赤道沿线的八个正方形想象成一条带子。在菱面立方八面体中,还有其他方向的类似八个正方形的带子;在 ψρ 中,只有一条带子。八分之一的扭曲用三角形中断了其他正方形带。
ψρ 是唯一一个具有看起来都相同的顶点,但未能具有将每个顶点移动到任何其他顶点的完整对象对称性的凸多面体,使其成为唯一的凸伪均匀多面体。在这个类别中,它有一个非凸的同伴。我应该注意到,虽然大多数数学家都同意阿基米德这个术语应该仅指阿基米德列出的 13 个多面体,即满足全局对称条件的多面体,但也有不同意见者。阅读布兰科·格林鲍姆的文章“一个持久的错误”以了解该观点。
当我思考 ψρ 时,我发现自己屈服于那种过于人性化的拟人化诱惑。我将 ψρ 想象成一个被排斥的人。他们试图融入,抛光他们的面,磨尖他们的顶点,试图和他们更完美的兄弟姐妹菱面立方八面体,甚至笨拙的截角四面体一起坐在午餐桌旁。但他们就是无法融入。又经历了屈辱的一天后,他们对着镜子看着自己,雨水从他们身后的窗户上滴落,映照出他们的眼泪。“为什么是我?”他们问道。“我的父母试图通过谈论丑小鸭来安慰我,但我没有完美的立体可以成长为!”他们不知道约翰逊家族一直在寻找一个出生时失踪的多面体。现在我们已经从汉斯·克里斯蒂安·安徒生转向牛奶盒上的脸。
但也许我的性格描述是错误的。ψρ 是班级小丑,嘲笑那些认为自己已经弄清楚一切的人吗?或者他们是勇敢的梦想家,他们推动了界限,并教会我们什么是可能的,是在灰色工业反乌托邦中教导我们不必如此的无畏、色彩鲜明的个体吗?在我的世界里,我认为 ψρ 更倾向于小丑。就在你认为你可以对阿基米德立体给出简短、简单的解释时,你必须开始描述一个技术条件,而这个条件仅仅是因为这个例子才是必要的!我仿佛看到了 ψρ 在窃笑,等待我落入陷阱,这样他们就可以爆发出来,大喊一声:“抓到你了!”
阅读更多关于我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 具有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔子 庞加莱同调球面 科瓦列夫斯卡娅陀螺 一个 6 孔环面 实射影平面 一维球面 尼斯湖水怪 科赫雪花 双圆柱 悬链面 SO(3)