本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
上周,在抗衰老研究公司Sens工作的生物学家奥布里·德·格雷报告说,他在大约60年来首次在哈德维格-尼尔森问题(也称为平面着色数问题)上取得了突破。
平面着色数是给平面上所有点着色所需的最小颜色数,以便没有两个正好相隔一个单位的点具有相同的颜色。自从这个问题被提出以来,数学家们就知道这个数字在四到七之间。德·格雷最近的论文表明,至少需要五种颜色,从而提高了下限。我为Quanta Magazine撰写了关于这个问题和最近进展的文章。
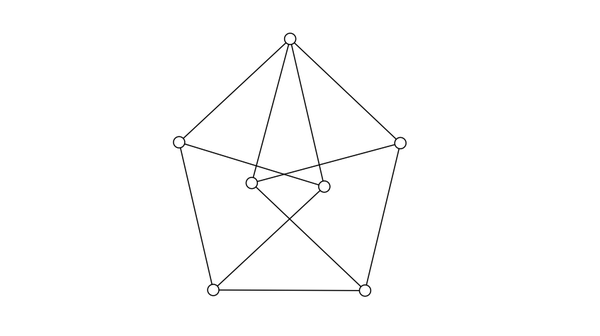
德·格雷通过找到一个具有单位长度边(或单位距离图)的图,证明了平面着色数必须至少为五,该图需要五种颜色。为此,他从一个名为莫泽纺锤体的小图开始。
支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的重大故事的未来。
莫泽纺锤体有七个点,可以放置成其 11 条边都具有相同的长度,使其成为单位距离图。需要四种颜色来确保莫泽纺锤体的任何两条边都不会连接两个颜色相同的点,这使得四成为哈德维格-尼尔森问题的下限。莫泽这个名字来源于利奥·莫泽和威廉·莫泽兄弟,他们也是数学家,并在 1961 年撰写了关于平面着色数的文章。
为了找到他最初的不可四着色图,德·格雷决定尝试组装具有大量边和莫泽纺锤体的图,看看他是否最终可以对着色施加足够的约束,以至于找不到四着色。它奏效了!莫泽纺锤体——以及大量的聪明才智和好运——帮助他找到了一个不可四着色图。
但我喜欢莫泽纺锤体不仅仅是因为它是一个优雅、有用的图,用于解决哈德维格-尼尔森问题。它也是一个可以用来研究四色定理的例子,四色定理是另一个与图着色相关的问题。
四色定理指出,平面或地球仪上的任何地图都可以着色,以便没有两个共享边界的国家具有相同的颜色。(尽管这个问题是用制图学的语言提出的,但制图师们集体打了个哈欠。他们在绘制地图时通常不会约束自己那么多,并且对着色的理论数学约束并不特别感兴趣。)用图论的语言来说,四色定理指出,每个平面图的顶点都可以使用四种颜色着色,以便没有两个相邻的顶点具有相同的颜色。
乍一看,您可能会想知道为什么哈德维格-尼尔森问题与四色定理不同,甚至比四色定理更容易。毕竟,这两个问题都涉及平面中的图。令人困惑的是,平面中存在非平面图。平面图不是您可以在平面上绘制的任何旧图,而是您可以在平面上绘制的边不交叉的图。
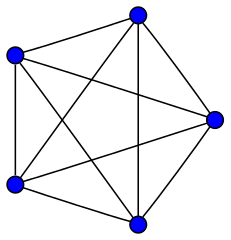
K5,即 5 个顶点的完全图,是非平面图。你能否说服自己,没有办法在平面上摆动这些边,使它们不交叉?致谢:Koko90 Wikimedia (CC BY-SA 3.0)
莫泽纺锤体也是一个平面图,因此它也可以用来证明平面图着色需要四种颜色。 现在我故意有点调皮了。这篇文章顶部的莫泽纺锤体的图片不是平面图。有四个地方边交叉,你无法在保持边长的同时解开它们。因此,莫泽纺锤体既是单位距离图又是平面图,但不是同时!我认为这是一个极好的数学玩笑。(顺便说一句,既是单位距离图又是平面图的图称为火柴棍图,因为您可以使用火柴在桌子上组装它。)
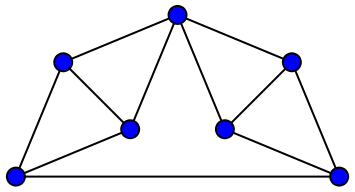
莫泽纺锤体作为平面图。边不再交叉,但其中一条边现在比其他边长得多。致谢:David Eppstein Wikimedia (CC0 1.0)
每当我听到“纺锤体”这个词时,舒伯特的歌曲《纺车旁的格丽卿》(Gretchen at the Spinning-Wheel)就会在我脑海中响起。我想不出一个可爱的方式将这首歌融入到一篇关于莫泽纺锤体的文章中,但这并不意味着您应该被剥夺聆听无与伦比的杰西·诺曼演唱这首歌的乐趣。
阅读更多关于我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的线 有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫链接的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔子 庞加莱同调球面 科瓦列夫斯卡娅陀螺 一个 6 孔环面 实射影平面 一维球面 尼斯湖水怪 科赫雪花 双圆柱 悬链线面 SO(3) 伪菱形立方八面体