本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
你听说过巴德尔-迈因霍夫现象吗? 如果没有,我相信在不久的将来你会听到更多次。这是一种认知现象,有时被称为频率错觉,它会在你第一次听到或注意到某件事之后出现,你会突然在短时间内多次听到它。
尼斯湖水怪空间最近让我经历了巴德尔-迈因霍夫现象。不久前,我偶然发现了一篇标题中就带有这个空间的论文,显然这个异想天开的名字吸引了我的眼球。我决定写一篇关于它的文章,当我开始写这篇文章时,另一位数学家在推特上谈到了它。这只有两次,但它发生在我作为数学家的生涯中十多年从未遇到过它之后。
你可以通过在规则的二维平面上添加柄来构建尼斯湖水怪。为了创建一个数学柄,你从平面上切出两个圆盘,并在它们之间粘上一个圆柱体。除了美观之外,柄还使平面更易于携带。(也许这个空间更好的名字应该是无限手提箱或可打包平面。)如果一个柄很好,为什么不添加更多呢?甚至无限多个?一些富有想象力的数学家决定将这个空间称为尼斯湖水怪,因为它像极了苏格兰神话野兽的模糊照片。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
我不知道是否有关于奈西是变形者的传说,但数学版本对我来说似乎就是这样。或者也许我应该把它看作是穿着戏服。我刚了解尼斯湖水怪曲面,就了解了一些其他名字引人入胜的数学空间:雅各布天梯、无限丛林健身房和无限监狱牢房窗户。
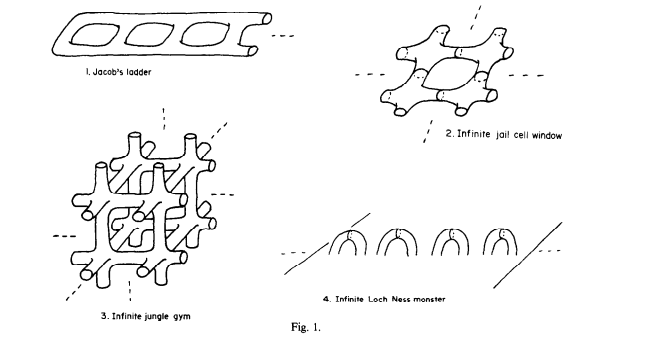
图片来源:Ian Richards 的论文 “论非紧曲面的分类”,《美国数学学会汇刊》第 106 卷,第 2 期,1963 年。
事实证明,这四个空间在拓扑上是等价的!(当数学家、老师或作家说“事实证明”时,你应该总是抱有怀疑。他们可能正在掩盖一些细节,而“事实证明”这句话原来是一张相当大的地毯。天哪,我又来了。)粗略地说,如果可以通过拉伸和挤压(没有撕裂或粘合)将一个空间变形为另一个空间,则两个空间在拓扑上是等价的。有一个数学笑话,拓扑学家无法区分甜甜圈和咖啡杯,因为它们都有一个孔。

马克杯和甜甜圈拓扑等价性的演示。图片来源:Lucas V. Barbosa Wikimedia PD-self
与甜甜圈和咖啡杯不同,这四个空间的拓扑等价性对我来说一点也不明显。丛林健身房有一个三维的感觉,而监狱牢房窗户有一个二维的感觉,雅各布天梯更像是一维的。
最初的震惊过后,我试图思考这三个非常不同的空间如何可能是等价的。我已经得出结论,这个空间有两件事要告诉我:端的拓扑概念有多重要,以及我对无限空间的有限直觉的局限性。
当我还是一名卑微的二年级研究生,并且刚刚开始阅读我导师领域的论文时,我不断遇到一个我不理解的词:端。显然我知道这个词在英语中的意思,但它在数学上被使用,我无法理解它的数学含义。那是其中一次,我可以几乎根据这个词的日常含义来理解它,但又不太对劲。
在拓扑学中,当你开始谈论无限曲面时,端这个词就会出现。较小的拓扑曲面,我们称之为紧致曲面,有一个很好的分类:它们都是环面和射影平面的组合。事实证明(我们又来了),这些无限怪物也有一个分类,这次是基于端。
端的基本思想是,它是在曲面上走向无穷远的一种方式,或者,如果你对“走向无穷远”的想法没有共鸣,那么它就是一种远离曲面任何有限、包含部分的方式。从一个简单的例子开始,实数线有两个端。如果你移除实数线的一些连通的、有限的块,就会有两条独立的射线,一条向正方向延伸,另一条向负方向延伸。如果你在正方向侧,你永远无法到达负方向侧,反之亦然。另一方面,二维平面只有一个端,因为如果你移除平面上某个地方的连通块,你将能够从平面剩余部分的任何点到达任何其他点。
非紧曲面(如尼斯湖水怪)的分类定理(pdf)指出,如果两个流形的某些端行为相同,则这些流形是相同的。 “行为”变得有点技术性,但基本上你需要流形具有相同的端数量、亏格(孔洞数量)和可定向性。
这就是我们如何看到我们的四个无限曲面实际上是相同的。它们都只有一个可定向的端,其中有无限多个孔洞。为了看到这一点,想象一下移除任何一个空间的某个中间部分,并想象一下使移除的中间部分越来越大。对于任何一个空间,你都可以看到剩余部分是可定向的(你永远不会开始在曲面上的某个地方行走,最终意外地倒着回到同一个地方),有无限多个孔洞,并且只有一个部分。换句话说,只要坚持不懈,你就可以从剩余部分的任何部分走到任何其他部分。
不得不相信定理的话说这四个空间在拓扑上是相同的,这有点令人不满意,但我认为我现在就是这样。即使我可以可视化将任何两个具有相同孔洞数量的有限曲面相互转换的拓扑变换,我也很难相信当我们试图将它们推得越来越远时,这些变换不会变得太疯狂。就目前而言,我只能相信这个定理。但我必须承认,Spencer Dowdall 的这张将奈西描绘成雅各布天梯版本曲面的图片有所帮助。
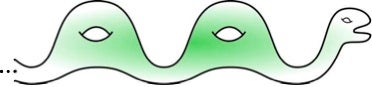
图片来源:Spencer Dowdall
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 具有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长直线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔子 庞加莱同调球 科瓦列夫斯卡娅陀螺 一个 6 孔环面 实射影平面 一维球面