2017年11月30日

我最喜欢的几个空间：科赫雪花

最具节日气氛的分形一览

科赫雪花可以平铺平面。它是您节日包装纸或饼干的完美图案！

大卫·爱泼斯坦 *维基共享资源*

本文发表于《大众科学》的前博客网络，反映了作者的观点，不一定代表《大众科学》的观点。

如果你曾在数学课上涂鸦，你可能偶然发现了科赫雪花。你可以从一个等边三角形开始制作它。然后取六个等边三角形，每个三角形的大小是原始三角形的 1/3，并将它们粘在每条边的中间三分之一处。现在冲洗并重复。再重复。再重复，直到永远。

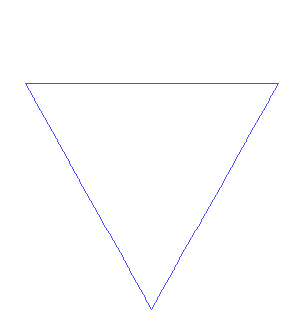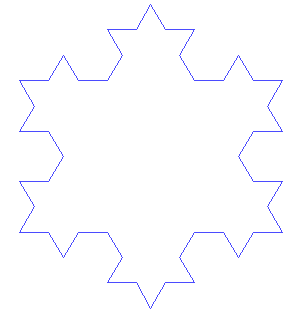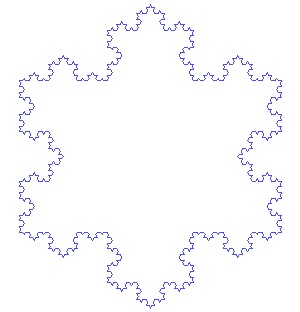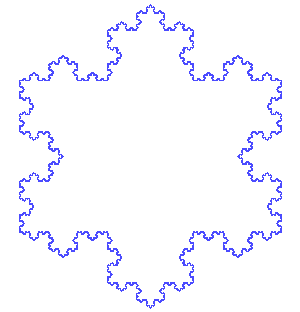
科赫雪花构造过程中的几次迭代。图片来源：安东尼奥·米格尔·德·坎波斯 *维基共享资源*

法语使用者（或者像我这样法语半吊子的人）可以在线免费阅读海尔格·冯·科赫于 1904 年发表的论文，其中首次出现了科赫曲线。（科赫曲线是科赫雪花的一侧；换句话说，你可以通过将三条科赫曲线粘在一起得到一个科赫雪花。）冯·科赫发明这条曲线是为了更直观、更直接地说明卡尔·魏尔斯特拉斯在几十年前记录的一种现象。这一切都归结为切线。光滑曲线有切线——在某一点接触函数并指向曲线在该特定点方向的直线。

关于支持科学新闻

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道订阅。通过购买订阅，您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。

在魏尔斯特拉斯发现他的“怪物”之前，一些数学家假设，如果一个函数是连续的——没有大的跳跃或间断——那么它几乎处处都有切线。可能这里或那里会有奇怪的角或尖点，但它们是孤立的。基本上，一个函数不可能处处都是角。魏尔斯特拉斯找到了反例，但它们很难理解和想象。科赫曲线在任何地方也没有切线，但冯·科赫的几何构造使其更容易理解。你在任何地方添加一个尖峰，你都在添加一个角。并且没有不带尖峰的线段。这个例子更具体，而且作为奖励，放在谢尔宾斯基圣诞树顶上非常漂亮。

像许多分形一样，科赫雪花突破了我们对维度的常规概念。雪花的边界既不是完全一维的，也不是完全二维的。它具有无限的长度，你可以通过注意到我们在每次迭代中将曲线的总长度乘以 4/3 来看到这一点，而无限多个 4/3 的乘积不是有限的。但它没有面积。（指的是边界。科赫雪花的内部是二维的，并且具有明确定义的面积。）

巧合的是，当我正在写这篇文章时，我的朋友，布朗大学的数学家凯蒂·曼恩，分享了科赫雪花的一个重要的实际应用：科赫山核桃派。在Instructables 网站上，查尔斯·福尔克斯描述并记录了他制作巨型科赫山核桃派的冒险经历。（如果我的粗略计算是正确的，它包含大约 5 打鸡蛋和 10 磅山核桃！）他指出，如果你制作一个半径非常大的传统圆形馅饼 R，“馅料的量与 R² 成正比，而馅饼皮仅线性增长，因此随着馅饼变大，酥脆的馅饼皮完全被奶油馅料所淹没。” 另一方面，科赫版本的馅饼皮的增长速度比线性增长更快，这使得喜欢馅饼皮的人可以在他们的馅饼中吃到更多的馅饼皮。

科赫山核桃派在特制烤箱中烘烤。在 Instructables 上查找更多科赫派的图片，以及Google 相册。图片来源：查尔斯·福尔克斯

福尔克斯报告说，用金属制作科赫派的烤盘帮助他对曲线具有许多没有切线的点意味着什么有了更直观的理解。他写道：“我的意思是，你认为你对数学分析有相当好的理解，但是除非一块具有非常高的周长与表面积比的金属撕裂你的肉体，否则你真的会错过对几乎处处缺乏连续导数的物体的直观理解。”

科赫雪花派是一项崇高的事业，但我认为它可以改进。馅饼皮虽然尺寸比例很好，但还是粘在边缘上。对于这么大的馅饼，径向馅饼块是笨拙的，如果不是完全不可能的话，所以拿到内部块的人仍然会感到沮丧和没有馅饼皮。

但是科赫雪花的另一个特性可以提供帮助。雪花可以自镶嵌。如果你取六个较小的科赫雪花副本并将它们粘在每个臂中，你将在中间留下另一个科赫雪花。它比臂中的雪花更大，但形状相同。你可以再次用更小的雪花来平铺内部的雪花，以此类推，而不是让内部的雪花保持原样。

用许多尺度较小的科赫雪花对科赫雪花进行镶嵌。现在想象一下，如果这些边界是由美味、酥脆的馅饼皮制成的。图片来源：埃德蒙·哈里斯 *宇宙的图案*，埃德蒙·哈里斯和亚历克斯·贝洛斯合著的数学涂色书

以馅饼的形式，这表明你可以在整个馅饼中构建分形馅饼皮墙，更均匀地分配馅饼皮。事实上，如果你用更小的雪花平铺内部的雪花，以及这些雪花的内部雪花，以此类推，你甚至可以满足最喜欢馅饼皮的人。