2015年9月29日

我最喜欢的几个空间：有两个房间的房子

理解一个数学对象意味着什么？直到我自己建造了它，我才真正相信存在有两个房间的房子。

作者：伊芙琳·兰姆

本文发表于《大众科学》的前博客网络，仅反映作者的观点，不一定反映《大众科学》的观点。

一想到有两个房间的房子，我就忍不住想到约翰福音 14:2：“在我父的家里，有许多房间。” 这个拓扑学的例子比上帝的国度要谦虚一些。毕竟，只有两个房间。更合适的经文是这样的：在宾的房子里，有两个房间。如果不是这样，哈彻会告诉你如何建造它吗？

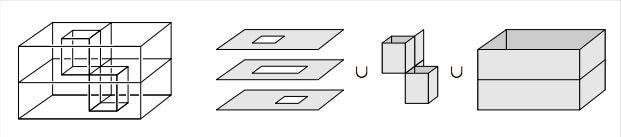
有两个房间的房子有时被称为宾的房子，以R. H. 宾的名字命名，他是第一个描述这个空间的数学家。但像许多数学专业的学生一样，我第一次在艾伦·哈彻的代数拓扑学书中遇到了它。他给了我们以下关于这个空间的图片和定义。

支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道：订阅。通过购买订阅，您正在帮助确保有关塑造我们当今世界的发现和想法的有影响力的故事的未来。

要建造这个空间，首先从一个盒子开始，盒子被一个水平矩形分成两个腔室，这里的“矩形”我们不仅指矩形的四个边，还指它的内部。从盒子外部进入两个腔室的通道由两个垂直隧道提供。上部隧道是通过从盒子的顶部冲出一个正方形，然后在正下方从中间水平矩形冲出另一个正方形，然后插入四个垂直矩形，即隧道的壁来制成的。这个隧道允许从盒子外部进入下腔室。下部隧道以类似的方式形成，提供进入上腔室的通道。最后，插入两个垂直矩形以形成两个隧道的“支撑壁”。因此，由此产生的空间 X 由三个与环域同胚的水平部分加上形成两个腔室壁的所有垂直矩形组成。

如果你的眼睛有点发花，你并不孤单。图片和描述很难理解。在我们尝试理解空间本身之前，我们应该弄清楚我们为什么要费心研究它。哈彻用它作为一个“可收缩但并非以任何显而易见的方式”的空间的例子。

“可收缩”是拓扑学的简写，意思是“像一个点”或者，不客气地说，“无聊”。如果一个空间可以被压缩成一个点而不会撕裂空间或粘合它的任何部分，那么这个空间就是可收缩的。例如，一个实心球是可收缩的，因为它即使是三维的而不是像点那样的零维的，它也可以被缩小到一个点，而不会撕裂或塌陷它的任何有趣的特征。因此，对于某些拓扑学目的，它非常接近于一个点，以至于我们不妨假设它是一个点。

哈彻断言，有两个房间的房子，就像一个实心球一样，也等价于一个点，尽管不那么明显。房子只是一个门面。它看起来好像有洞，但从拓扑学的意义上来说，它们实际上并不存在。

长期以来，我对有两个房间的房子持怀疑态度。我只是看不出如何在不改变其拓扑结构的情况下将其压缩成一个点。我接受了哈彻的说法，但直到我自己制作了它，我才真正相信它的可收缩性。上学期春假前一天，我带了一些黏土到我的拓扑学课上，我们制作的东西之一就是有两个房间的房子。当我们完成时，我觉得我真正理解了这个空间。

在这里，我可以告诉你我是如何看到这个空间是可收缩的，但我不会这样做。我认为看到它的最好方法是用黏土或你手头的任何柔软材料制作它。哈彻的图表和描述给出了一个很好的配方，而且我从个人经验中知道，本科生甚至像我这样的博士后都可以很好地遵循这些说明来创建一个令人信服的有两个房间的房子，尽管我必须承认我们的屋顶漏水。

如果你想走捷径，北爱荷华大学数学家塞隆·J·希奇曼的儿子，12 岁的大卫·希奇曼制作了一个有趣的关于在 Minecraft 中建造它的视频，肯·贝克在博客 Sketches of Topology 上写了关于它的文章。在那里，他用不同的方式描述了它。

你知道吗，与其握手，不如抓住彼此的手腕？你的拇指几乎但并没有完全够到你的手指？宾的两手手套会很合身。

显然，有两个房间的房子（或者我可能不得不开始称之为的两手手套）激发了我的宗教思想。当我写这篇文章时，我意识到，就像多疑的托马斯一样，我需要在相信它之前用手感受这个空间。“你因为看见了我才信，那没有看见就信的有福了。” 耶稣对托马斯的回答可能适用于门徒训练，但我认为它对拓扑学来说是倒退的。那些不得不拿出一些黏土或打开 Minecraft 并创造出有两个房间的房子才相信它的人是有福的。