本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
当我前往圣艾夫斯时,
我遇到一个有七条线的平面,
每条线都有
七个三个点,
(但总共有七个点),
这首诗不太适合法诺平面。
我谦虚地认为法诺平面是最小的有趣空间。可能有一个厚颜无耻的归纳证明与此相反,但一个单独的点,或几个孤立的点,并不能构成一个有趣的例子。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑订阅来支持我们屡获殊荣的新闻报道。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
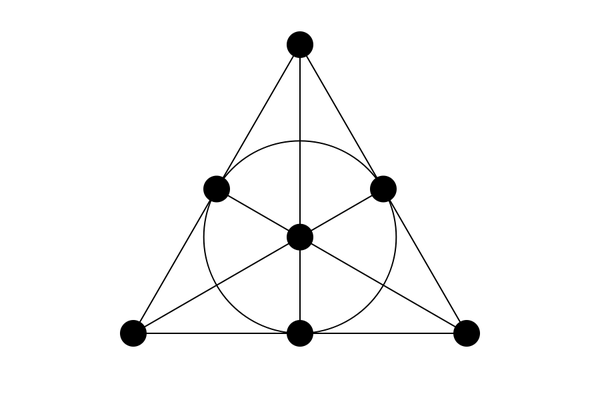
法诺平面有七个点,它们位于七条线上。仅此而已。它是射影平面最小的可能示例。
您是否曾经觉得平面上有些线相交,而有些线不相交,这有点令人扫兴?多么随意!射影平面允许您通过强制线相交来消除这个恼人的问题。
要成为射影平面,必须满足几个条件。
每对点都由一条线连接。
每条线都与其他每条线相交。
存在四个点,使得没有一条线包含其中多于两个的点。 (第三个条件并非总是列出,但它排除了诸如一条线上有 2 个点或几条线穿过一个点之类的愚蠢情况。)
有时数学是关于理性战胜直觉,而当您思考射影几何时,就是其中一些时候。(公平地说,有时射影几何看起来非常直观;毕竟,它的应用之一是在透视绘图中。) 您可以通过为每组平行线添加一个“无穷远”点,将欧几里得平面变成射影平面。因此,水平线有一个无穷远点,垂直线有一个点,与水平线逆时针成 47.322 度的线有一个点,依此类推。然后,您声明无穷远点的集合为无穷远线。如果您思考一段时间,您可以说服自己,这满足所有要求。
如果无穷远线上有无限多个点对您来说太丰富了,那么法诺平面是一个更便宜的替代方案。很容易看出点和线是如何相交和相互作用的。
法诺平面挑战直觉。 当您看到它的图片时,您会非常容易理解地认为它有无限多个点。毕竟,它有 7 条线,我们都知道线段,即使是非常短的线段,也有无限多个点。
不!数学是独裁统治,而我们是独裁者。 我们声明这七个点是仅有的七个点。线不是由点组成的,它们只是线。 法诺平面的另一个违反直觉的方面是,其中一条线看起来像一个圆圈,至少在大多数描绘中是这样。但是,如果您已经接受了线不是由无限多个点组成的观点,那么您应该不难说服自己,圆圈实际上是一条线。
法诺平面是最小的有限射影平面。您可能想知道其他射影平面有多大。如果我们想让每条线上有 4 个点而不是 3 个,我们可以找到一个吗?弄清楚射影平面可以有多大出乎意料地不简单。(关于术语:法诺平面被称为 2 阶,因为每条线上有 2+1=3 个点,并且每个点都在 2+1=3 条线上。一般来说,如果每条线上有N+1 个点,并且每个点都在N+1 条线上,则射影平面的阶数为N。阶数为N的射影平面有N2+N+1 个点。)我们知道存在每个素数阶和每个素数幂阶的射影平面,但对于其他数字,我们仍然有很多工作要做。仅在九十年代 研究人员才最终证明不存在 10 阶射影平面 (pdf),例如,而对于 12 阶,问题仍然悬而未决。
尽管有限射影平面似乎是纯粹 公理化思维战胜任何现实暗示的胜利,但法诺平面及其亲属在赌博中(尤其是所有事物中)有一些令人惊讶的应用。我第一次在乔丹·艾伦伯格的书《How Not to Be Wrong》中读到它们。他给出了一个彩票的例子,其中从总共 7 个数字中选出 3 个数字。玩家通过匹配所有 3 个数字或匹配 2 个数字来赢得较小的奖品来赢得头奖。
7 个数字中选 3 个数字共有 35 种可能的组合,因此您只有 1/35 的机会赢得头奖。但是,借助法诺平面,您可以提高匹配 2 个数字的机会。诀窍是购买几张彩票,并避免在任何两张彩票上出现相同的数字对。您不想同时购买 123 和 234,因为如果两个数字是 2 和 3,您就重复覆盖了它两次。这意味着奖金翻倍,但也意味着您将不会获得不同数字对的任何奖金。
要用法诺平面赢得彩票,请用 1 到 7 的数字标记每个点,并读出每条线上的数字。我得到了 123、147、156、246、257、345、367。
如果您检查这些数字,您会发现每对数字都恰好出现一次。无论头奖是什么,我们都将至少匹配三个数字中的两个。如果您的点标记方式与我的不同,您将获得不同的数字集合,但它仍然具有相同的属性。
没有多少彩票只抽取 3 个数字,但是通过一些谨慎和计算机能力,这个想法可以扩大规模。当然,彩票支付系统不太可能有利可图到足以证明即使是涉及射影平面的巧妙策略也是合理的,但如果您有兴趣,艾伦伯格讲述了 Cash WinFall 的故事,该彩票的奖金足以让一些麻省理工学院的学生赢得一些真金白银。
要了解法诺平面、拉丁方、环面拓扑、纠错码和许多其他主题之间的联系,请查看弗吉尼亚理工大学的以斯拉·布朗的这两篇文章:(7,3,1)的众多名称 和 (7,3,1)的更多名称。如果您喜欢的话,法诺平面还可以帮助您记住八元数中的乘法运算方式,并且我忍不住指出它与死亡圣器的符号惊人地相似。

公理几何学对石头、魔杖或隐身衣几乎无话可说。图片:公共领域,来自 维基共享资源。
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的线 具有两个房间的房子 环面 三环面 莫比乌斯带 长线 空间填充曲线