本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
今年四月,我终于第一次读了《沃特希普高地》,我的一个读书小组讨论了《野兔之年》(阿尔托·帕西林纳写的一本奇怪的小书,我发现很搞笑,但我的小组的其他大多数人不喜欢),当然那也是复活节,它的世俗庆祝活动以兔子为中心,不知何故兔子还下蛋。有什么比在数学上了解杜阿迪兔子更能进入兔科动物的春季精神的方式呢?
像我最近许多最喜欢的空间一样,杜阿迪兔子是一个以一位法国人名字命名的分形(例如,法图煎饼和曼德勃罗集)。它的同名者阿德里安·杜阿迪(1935-2006)研究了复动力系统和曼德勃罗集,后者是他为了纪念曼德勃罗而命名的。我不知道是谁决定用杜阿迪的名字来命名这个分形,但那一定是某个非常钦佩他的“兔子”先生。
为了理解杜阿迪兔子,我们首先要了解曼德勃罗集和许多朱利亚集之间的关系。我在关于曼德勃罗集和法图煎饼的帖子中写到了这种关系,但如果您不想去阅读那些文章,那么主要思想是曼德勃罗集中的每个点c都与形式为f(z)=z2+c的函数相关,并且我们关心迭代这些函数时会发生什么。您将数字z=0代入开始,然后将输出重新代入函数,依此类推。如果迭代保持有界,则数字c在曼德勃罗集中。如果迭代增长非常大,则数字c不在曼德勃罗集中。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们今天世界的发现和想法的具有影响力的故事的未来。
您对曼德勃罗集研究和玩耍得越多,您就会越发明白这个形状不仅仅是一个漂亮的数学作品,可以作为书呆子纹身。曼德勃罗集和称为填充朱利亚集相关的其他分形之间存在许多美丽的联系。函数的填充朱利亚集是迭代下保持有界的点的集合,而曼德勃罗集对应于数字c,对于这些数字,函数f(z)=z2+c的填充朱利亚集是一个整体,而不是分散的、像灰尘一样的物体。(也许是灰尘兔子?)
我设想曼德勃罗集中的每个点都举着一个小牌子,上面画着它的填充朱利亚集。如果您在曼德勃罗集中挑选出一个点,您就知道它将举着一个牌子,上面有一个完整的填充朱利亚集,如果您拿起两个附近点的牌子,它们可能看起来不会太不一样。
杜阿迪兔子是函数f(z)=z2+c的填充朱利亚集,其中参数c近似为-0.12256+0.74486i。(这里,像我帖子中通常一样,i=√-1。)
每当我写关于曼德勃罗集或相关分形的文章时,我都要推荐霍莉·克里格的Numberphile关于它的视频。今天我还想推荐该视频的第二部分,她在其中分享了关于填充朱利亚集的更多信息,并提到了兔子及其一些同类。
除了它看起来有点像兔子这一事实——老实说:它与任何兔形目动物的相似之处充其量只是印象派的——为什么要关心这个特定的朱利亚集?我不反对在数学上寻找云朵中的形状,但是否有任何理由认为,在这个浩瀚的填充朱利亚集海洋中,这个填充朱利亚集特别到足以拥有自己的名字?
是也不是。杜阿迪兔子有一个由三个点组成的循环,从0开始,在定义映射的特殊c下,这些点相互映射。事实上,这就是我们如何精确地计算出c。如果我们从0开始并迭代函数,将我们的答案重新代入,我们想要一个点循环,以便0转到第一个点,第一个点转到第二个点,第二个点转回0。我们知道,当我们将0代入函数f(z)=z2+c时,我们得到c。然后当我们迭代它,将c代入z时,我们得到c2+c。当我们将其重新代入函数时,我们得到(c2+c)2+c,并且因为我们希望循环闭合,所以我们将此数字设置为等于0。一点在线方程求解器之旅(因为谁有时间记住三次方程,即使它是用特扎韵诗写成的也很好听?)我们发现c可以近似为-1.7549、-0.12256+0.74486i或-0.12256-0.74486i。碰巧杜阿迪兔子对应于c=-0.12256+0.74486i。
因此,当我们固定c并查看函数f(z)=z2+c时,我们知道数字0、c和c2+c形成了一个漂亮的小循环,从一个跳到另一个。碰巧的是,兔子中的所有其他数字也被这个小循环吸引。这个点循环位于兔子的心脏、嘴巴和耳朵处(至少我是这样想象兔子的;它的解剖结构可以随意解读)。
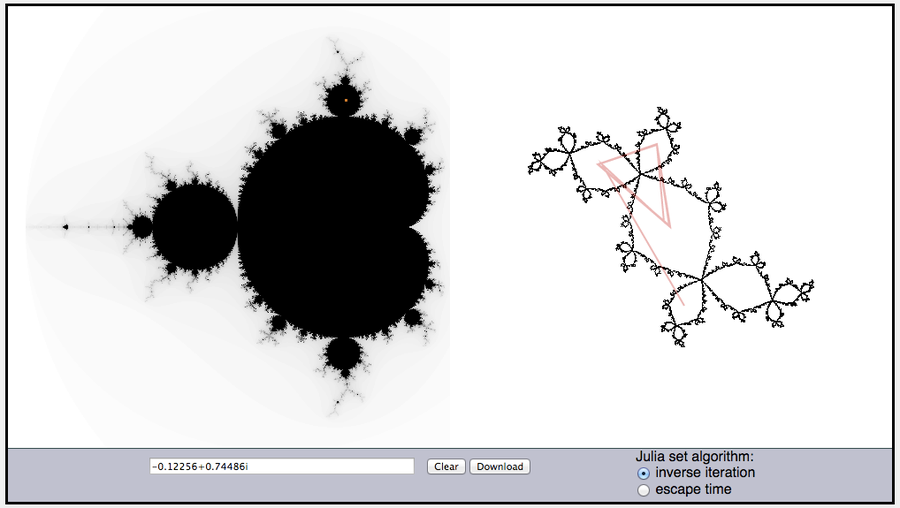
左图:曼德勃罗集,在点c=-0.12256+0.74486i处有一个红色小方块,它对应于杜阿迪兔子。右图:杜阿迪兔子,带有几条红色线段,显示了在映射f(z)=z2+c下点的轨迹。顶部的三角形顶点位于三个点0、c和c2+c处。
致谢:伊芙琳·兰姆,使用马克·麦克卢尔的朱利亚集生成器
然而,杜阿迪兔子远非唯一具有这种行为的分形。我找到了马克·麦克卢尔制作的一个有趣的曼德勃罗/朱利亚集探索页面,您可以在那里四处查看,看看这种行为发生在何处。(但请注意。该页面是一个相当深的兔子洞!)在那里,您可以在曼德勃罗集中点击以找到您最喜欢的朱利亚集,然后查看当您在曼德勃罗集中移动时它们如何变化。然后,一旦您找到喜欢的朱利亚集,您就可以在其中单击以查看内部的点如何跳跃。当您单击定义杜阿迪兔子的点c附近的任何位置时,您会看到一个外观相似的分形,并且您会看到类似的固定点三角形。杜阿迪兔子只是以0作为固定点的特殊兔子。麦克卢尔的交互式吸引盆地页面也以杜阿迪兔子为特色。
如果杜阿迪兔子对您来说还不够,还有一些其他“兔气十足”的朱利亚集可供选择。“反兔子”是兔子的反向图像,通过将参数c更改为-0.12256-0.74486i创建。“胖兔子”(或者我喜欢称之为“胖乎乎的兔子”)对应于附近的c,约为-.0125+.655i。也许您会更喜欢霍莉·克里格几个月前在Twitter上分享的另一个美丽的集合:“由胖反兔子组成的瘦兔子”,正如她所描述的那样。我甚至找到了一篇关于“扭曲兔子”(与杜阿迪兔子相关)的论文。(这篇论文相当技术性,但它有一些漂亮的图片。)
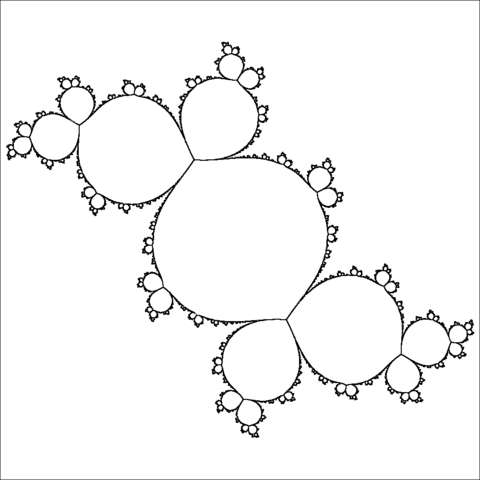
胖兔子,或胖乎乎的兔子,是函数f(z)=z2+-0.12565651+0.65720i的朱利亚集。致谢:Adam Majewski Wikimedia(CC BY-SA 3.0)
如果您希望您的兔子分形实际上与兔子有相似之处,凯瑟琳·林赛写了一篇论文,详细介绍了如何用复杂函数的朱利亚集来近似甚至非常复杂的图片。几年前我写过关于这项工作的文章。她和合著者马利克·尤尼西最近发表了一篇扩展这项工作的论文。
有了所有这些可能性,希望你能找到一些能打动你的分形兔子。
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 有两间房子的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫链接的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF度量 曼德勃罗集 法图煎饼 伪球面