2018年1月31日

我最喜欢的空间之几：悬链面

庆祝可能是最简约的最小曲面

本文发表于《大众科学》的前博客网络，反映了作者的观点，不一定反映《大众科学》的观点

有点尴尬的是，我已经写我最喜欢的空间快三年了，但还没有包括任何最小曲面。我的导师Mike Wolf 研究最小曲面。虽然我最终没有进入那个研究领域，但我学到了一些基础知识，并且当我与我的学界同仁谈论他们的工作时，这个话题有时会被提及。所以这篇文章早就应该写了。

最小曲面的概念是，如果你给定一个边界曲线，那么就存在一个面积最小的曲面，其边缘就是该边界曲线。（这被称为普拉托问题，以物理学家约瑟夫·普拉托的名字命名，而不是因为曲面看起来像高原。）数学家和普拉托本人特别喜欢用肥皂泡作为例子。如果你从肥皂泡的金属丝框架开始，肥皂通常会呈现出一种形状，使以该金属丝边界为边界的薄膜面积最小化，正如 Henry Segerman 在这段视频中演示的那样。

关于支持科学新闻事业

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻事业订阅。通过购买订阅，您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的有影响力的故事。

如果您想更深入地了解肥皂薄膜和最小曲面，请查看我的导师就此主题所做的演讲。今天，术语“最小曲面”指的是任何在局部最小化面积的曲面。“局部”一词意味着，如果我们观察曲面上任何点周围的小区域，就没有办法减少该小区域的面积。这首先意味着我们不再需要在曲面上有一个边界。但是，也存在一些边界，允许多个不同的局部面积最小化曲面跨越它们，正如 Segerman 在视频中演示的那样。

悬链面是在微分几何课程中您将遇到的最早的最小曲面之一。如果您想用肥皂薄膜制作一个，您需要将边界制成两个彼此平行且相隔很短距离的圆。

肥皂薄膜悬链面。图片来源：Blinking Spirit *Wikimedia*

悬链面也是通过绕轴旋转称为悬链线的曲线而获得的旋转曲面。（悬链线本身就很有趣，但那是另一个博客帖子的故事了。）

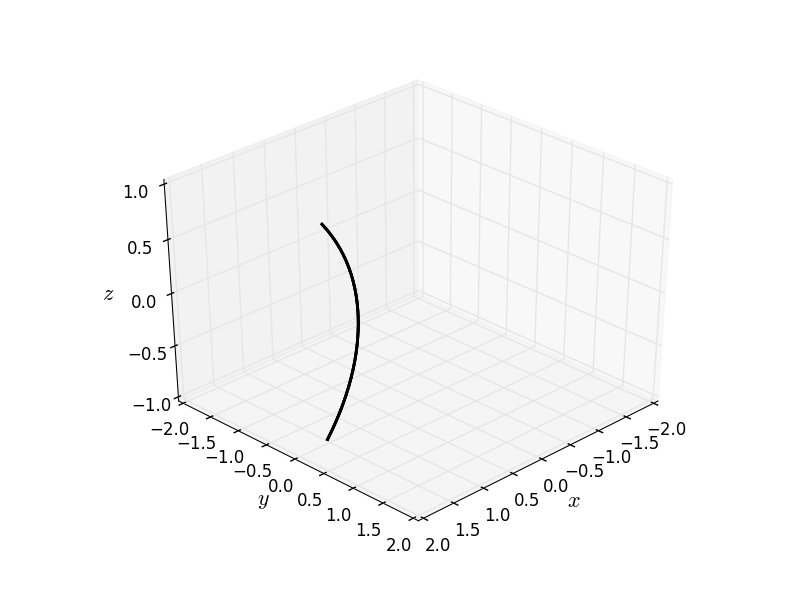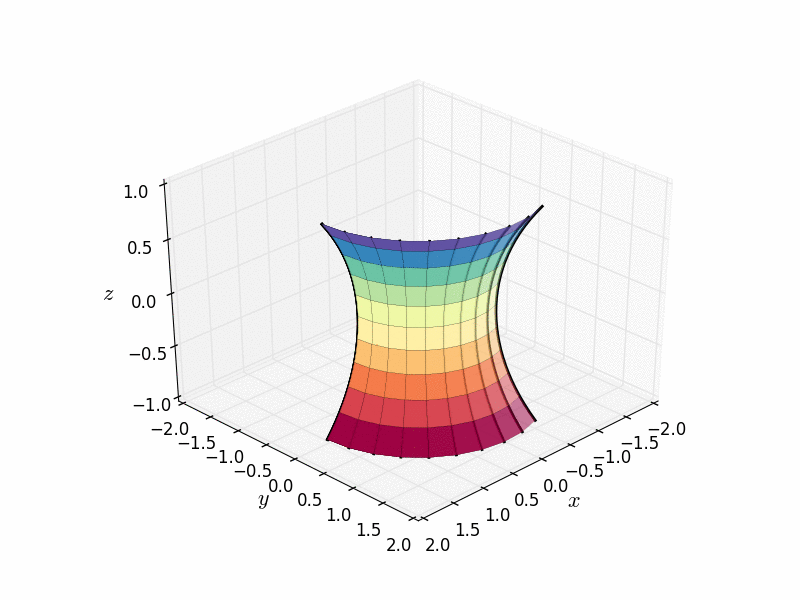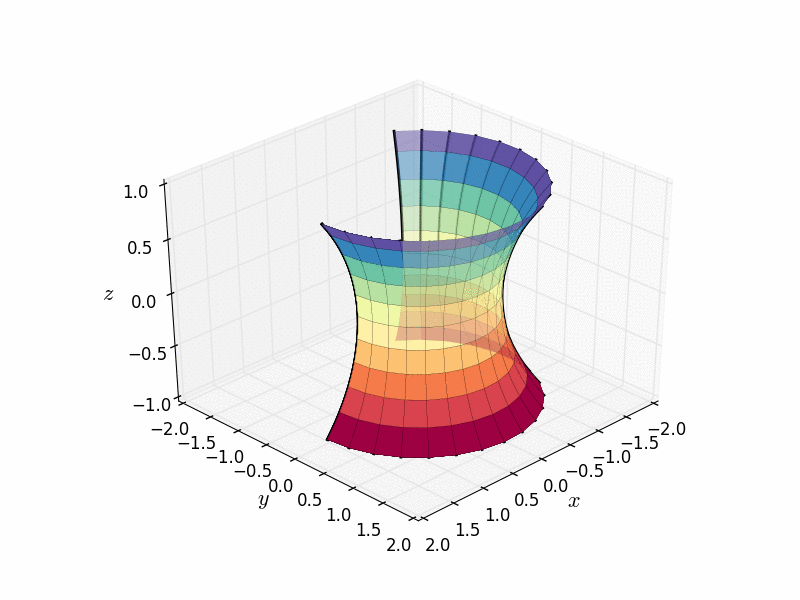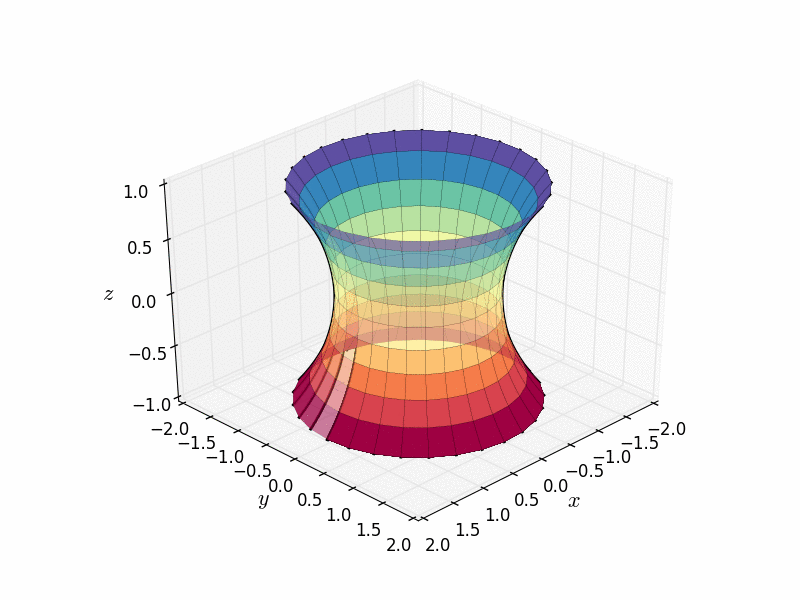
由悬链线作为旋转曲面创建的悬链面。图片来源：Nicoguaro *Wikimedia*(CC BY 4.0)

您可能会听到悬链面被称为“细腰圆柱体”，因为它像许多人的腰部一样向中间收缩。（我喜欢想象年轻的悬链面在谈论他们上周末是多么的“细腰”。）

通过检查悬链面，我们可以开始注意到最小曲面的另一个特征。首先，我们可以看看当我们将两个边界圆彼此移开时，肥皂薄膜悬链面会发生什么变化，如本视频所示。

一开始，悬链线只是略微弯曲。它几乎是一个规则的圆柱体。但是随着圆圈的移动，腰部变得更加明显。（最终，没有足够的肥皂薄膜来维持悬链面，因此它会破裂并塌陷以填充两个圆圈，但从数学上讲，我们将专注于它在悬链面构象中花费的时间。）在整个过程中，我们可以观察曲率如何变化。我在“我最喜欢的定理”Jeanne Clelland 那一集的节目注释中写了关于曲率的内容。在悬链面中，我们将观察连接两个边界圆的曲线的曲率和围绕悬链面腰部的曲线的曲率。

当圆圈之间运行的曲线更接近平坦时，腰部曲线也更接近平坦。当圆圈分开并且它们之间的曲线更弯曲时，腰部也变得更弯曲。碰巧的是，这两条曲线，一条从中点“向上”弯曲，另一条“向下”弯曲，总是完美地相互平衡。这不仅仅是碰巧适用于悬链面的巧合。事实证明，具有此属性的曲面（称为具有恒定平均曲率零）是表征最小曲面的另一种方式。在某些地方，它们可能非常弯曲，而在某些地方则更平缓地弯曲，只要曲率完美平衡即可。

悬链面本身是一种非常对称、可爱的形状，但它还有另一种超能力。只需剪开一刀并进行一些小心的操作，它就可以在不拉伸或挤压的情况下转变成（部分）螺旋面，另一种最小曲面。

悬链面和螺旋面之间的转换。图片来源：Wickerprints *Wikimedia*

1776 年，悬链面和螺旋面是被证明是最小曲面的第一个非平凡曲面。（平面或其一部分是平凡的例子。）自那以来的几个世纪里，数学家们发现了一系列越来越奇异的最小结构，它们具有奇特的自相交、重复部分或孔洞。但就优雅的简洁性而言，悬链面是无与伦比的。