本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
n个圆的花束在我心中占有特殊的地位。我想我应该说n个圆的花束们在我心中占有特殊的地位,因为对于每个整数n,都存在这样一个花束。这个空间也被称为n个圆的楔形或n个花瓣的玫瑰(尽管它通常看起来更像雏菊),它由n个在一点相遇的圆组成。我们从拓扑学的角度考虑这个空间,其中确切的形状和距离并不重要,所以在图片中,“圆”通常会稍微变形。否则,当我们试图在平面上绘制它们时,它们会重叠。
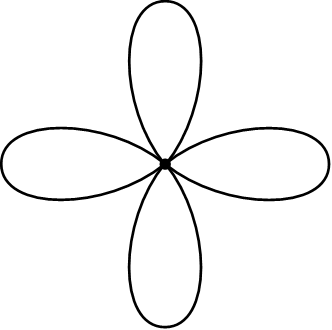
一个由4个圆组成的花束。来源:Jim Belk,维基共享资源
我如此喜爱这个空间的原因是,它是拓扑学产生代数洞察力的一个例子。代数,基本上是对称性和结构的研究,是拓扑学中一个非常有用的工具,但拓扑学在代数中应用的情况比较少见。为了理解原因,我们需要研究基本群。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
基本群是拓扑学家用来区分和描述空间的一个根本重要的工具。基本群描述了您可以在空间中绘制的环的种类。如果可以通过在空间中摆动一个环使其与另一个环重合,则认为两个环是相同的。磁盘或平面中的任何两个环都可以通过这种方式等价,因此它们的基本群非常无聊。但是在像环面(甜甜圈的表面)这样的空间中,存在一些不能相互摆动的环,并且基本群具有更多的意义。
在n个圆的花束中,可以通过环绕的圆、方向、次数和顺序来识别环。例如,在由2个圆组成的花束(即数字8)中,有一个环,它顺时针绕左边的圆一次,然后绕右边的圆一次。这个环与绕右边的圆然后绕左边的圆的环不同,因为空间中没有空间让您操作一个环并将其变成另一个环。(您可以使用橡皮筋来说服自己这个事实。)在下图中,顺时针绕左边圆的环标记为a,逆时针绕右边圆的环标记为b,我们定义a-1(发音为“a的逆”)为逆时针绕左边圆的环,b-1为顺时针绕右边圆的环。
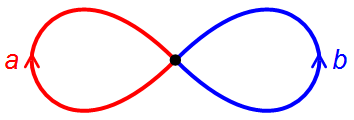
一个数字8,或由2个圆组成的花束。来源:Jim Belk,维基共享资源
数字8的基本群可以用a、a-1、b和b-1的所有有限字符串表示。(您应该稍微怀疑我偷偷地加入“有限”这个词,因为我从未告诉过您环的严格定义要求它具有有限的长度。现在我说了。)如果a旁边出现a-1,或者b旁边出现b-1,您可以将它们抵消。
描述数字8的基本群的精巧方法是由2个生成元生成的自由群。生成元是字母a和b,它们自动带有它们的逆元,而单词“自由”指的是,除了将一个字母放在它的逆元旁边,没有其他方法可以抵消任何相邻出现的字母组合。有些群可以发生这些抵消,但自由群不是发生这些抵消的地方。
正如数字8的基本群是两个生成元上的自由群一样,n个圆的花束的基本群是n个生成元上的自由群。在您使用这些花束来证明一个关于自由群的非常酷且至少对我而言是违反直觉的事实时,它似乎很普通:3个生成元上的自由群是2个生成元上的自由群的子群!更一般地说,n个生成元上的自由群是2个生成元上的自由群的子群。这对我来说是违反直觉的,因为看起来3个生成元应该比2个生成元给出“更大”的群,并且子群看起来比它们所属的群“更小”。但是当涉及到像自由群这样的无限事物时,这些直观的概念通常会被抛到九霄云外。
抱歉,拓扑学学生们,我不会告诉您如何使用圆的花束来证明3个生成元上的自由群是2个生成元上的自由群的子群。但是,一旦您掌握了正确的定理,这就是代数中一个事实的证明实际上从拓扑设置中出来的非常酷的例子。(这些定理做了很多繁重的工作来连接代数和拓扑学,所以它不是凭空产生的,但我仍然认为它非常酷。)
我在研究生院努力通过了拓扑学资格考试。(资格考试或初试是大多数研究生课程要求学生在正式进入学位研究和论文部分之前通过的考试。通常,学生应在研究生课程的第一年或两年内通过考试。)由于这种挣扎以及我花费在这些材料上的额外时间和精力,这可能是我今天仍然可以通过的唯一资格考试!考试前一晚我学习的最后一件事是教科书末尾关于自由群和n个圆的花束的一节。我认为我们在课堂上讲过这个材料,但当时没有记住。这可能是我第n次阅读该部分并试图理解它的一个相当大的n,但这次不同。我不认为天堂真的打开了,但我确实记得当我最终真正理解了本节中的大思想时,那种顿悟和轻松的感觉。第二天早上,考试碰巧有两个关于我刚刚学习过的材料的问题。我感到非常幸运,在晚上合上书本之前刚好学习了正确的东西,从那时起我就一直对圆的花束心存感激。
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 具有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长直线 空间填充曲线 瓦利斯筛 沿缝隙粘合的两个环面 空集 门格海绵 四个霍普夫链环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔 庞加莱同调球面 科瓦列夫斯卡娅陀螺 一个有6个孔的环面 实射影平面 一维球面 尼斯湖怪 科赫雪花 双圆柱 悬链面 SO(3) 伪菱形立方八面体 莫泽锭子 阿涅西的女巫 安托万项链