2017年12月30日

我最喜欢的空间：双圆柱体

这种形状也被称为牟合方盖或斯坦梅茨立体，最早在中国对球体体积的探索中出现

双圆柱体，牟合方盖，或斯坦梅茨立体。

Ag2gaeh Wikimedia(CC BY-SA 4.0)

本文发表于《大众科学》的前博客网络，反映了作者的观点，不一定反映《大众科学》的观点

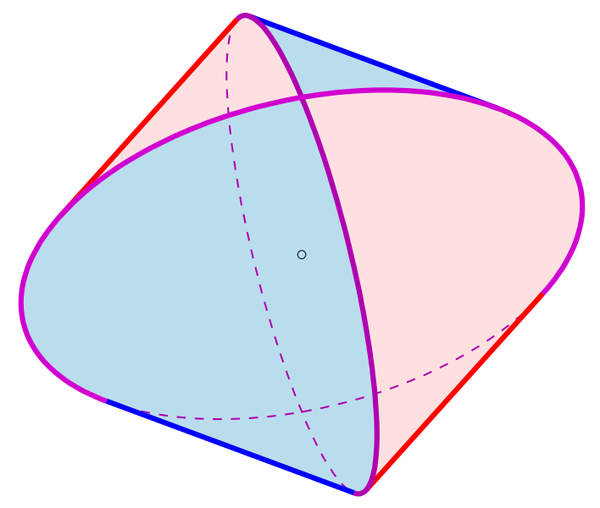
双圆柱体是一个可爱的小形状。它有正方形的横截面，但仍然令人愉悦地弯曲。它是你观察两个相同的实心圆柱体以直角相交时得到的形状。早期的中国数学家称这种形状为牟合方盖，有时翻译为“两个方形雨伞”，它也被称为斯坦梅茨立体。（人们也使用术语斯坦梅茨立体来指代由三个或更多，而不是两个，相交圆柱体构成的类似图形。）

一个动画展示了从两个相交圆柱体中出现的双圆柱体。来源：Van helsing *Wikimedia*(CC BY-SA 3.0)

这个物体出现在我最喜欢的卡瓦列里原理的例子中。卡瓦列里原理是指如果两个物体在每个高度的横截面积相同，则这两个物体具有相同的体积。（当然，有一些技术细节需要理清，以确保我们正确地测量横截面。）当你口头表达这个想法时，它似乎是显而易见的，但当你在实际中看到它时，可能会违反直觉。微积分老师喜欢用一堆硬币作为例子。你可以将它们整齐地排列成一个完美的圆柱体，或者用它们建造一个摇摇晃晃的塔。无论哪种方式，这都是同一堆硬币，所以这两个塔具有相同的体积。

关于支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道订阅。通过购买订阅，您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的想法的有影响力的故事。

一个非常英式的卡瓦列里原理演示，使用了英镑硬币。这两个塔有不同的形状，但体积相同。（而且成本也相同。）来源：Chiswick Chap *Wikimedia* (CC BY-SA 3.0)

你不是每天都能在计算中使用卡瓦列里原理，所以它总是感觉有点特别。Vsauce有一个关于餐巾环问题的有趣视频，这是该技术的一个令人惊讶的应用。

我最喜欢的关于双圆柱体的故事始于刘徽，一位生活在公元三世纪的中国数学家。他今天最出名的是他对《九章算术》（一部重要的早期中国数学著作）的广泛注释，以及他的使用内接多边形计算π的算法。刘徽使用了双圆柱体，或者当他研究球体的面积时。

思考球体的一种方式是将其视为一堆彼此堆叠的无限薄的圆片。最大的圆片在正中间，越靠近两极，圆片越小。

薄圆片构成一个球体。要制作双圆柱体，请将每个圆片替换为正方形。来源：伊芙琳·兰姆

要获得双圆柱体，只需将每个薄圆片替换为一个外接正方形。据我所知，刘徽是以这种方式提出双圆柱体的，他寻找的是一个包含球体的形状，而不是通过观察两个圆柱体的交集。但是，不难说服自己，这堆正方形与两个圆柱体的交集是相同的。首先，想象一下将一个球体放在双圆柱体的中间。现在想象一下，沿垂直于两个圆柱体的方向切割双圆柱体的横截面。每个横截面都将有一个双圆柱体的正方形外接球体的一个圆。（如果你难以想象，你可以随时拿起几个卫生纸卷筒，制作自己的双圆柱体。）

像刘徽一样，我们现在可以注意到，牟合方盖的横截面始终是一个外接圆的正方形。如果我们称圆的半径为r，我们可以得出结论，双圆柱体与球体的每个横截面的面积比为4r²:πr²，或4:π。现在，卡瓦列里原理意味着这两个物体的体积比也为4:π。

今天，这感觉就足够了。球体的体积公式是众所周知的，所以我们可以从那里开始。如果一个球体的体积为4/3πr³，我们可以得出结论，双圆柱体的体积为16/3r³。* 但这不是刘徽的起点。他实际上试图使用双圆柱体来获得球体的面积公式。不幸的是，他在那里卡住了。但这绝非小小的进步。正如林力扬和沈康身在一篇关于中国卡瓦列里原理应用的论文中写道：“尽管刘徽承认他无法继续证明球体的体积，但他已经用数学的严谨性分析了这个问题，并确定了困难的领域。” 在刘徽去世约200年后，祖冲之和他的儿子祖暅能够在他停下的地方继续前进，并使用双圆柱体完成了球体体积的计算。他们的方法涉及对双圆柱体的外接立方体的巧妙分解。

有关刘徽、祖冲之和祖暅在确定球体体积方面的工作的更多信息，请查看林力扬和沈康身的“中国卡瓦列里原理的概念及其应用”或T. Kiang的“一种古老的中国球体体积计算方法”。（前者似乎可以免费访问；后者可能需要付费。）您还可以通过Anthony Or的一些Geogebra工作表探索双圆柱体，其中一个工作表展示了一些立方体分解。

*本句已编辑以更正双圆柱体体积中的错误。