本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
啊,圆。它是数学的基石:优化问题的解决方案,周期函数的来源,我们可以绘制的最完美的对称形状之一,以及赋予本博客名称的单位根的栖息地。但它也很基础。当婴儿和幼儿学习形状时,他们的书——那些由无毒防水材料制成的书,因为它们被啃咬的次数和被阅读的次数一样多——里面都有圆形。圆形与字母、数字和颜色的名称一样,是他们开始理解世界的形成性组成部分。
数学家通常称圆为一维球体,或 S1。它被定义为平面上距离中心点 (0,0) 或原点正好 1 个单位的点集。(更严谨地说,这是单位圆。一般来说,圆可以是任何大小,并且位于平面上的任何位置。)我们可以很容易地将其描述为满足方程 x2+y2=1 的点集 (x,y)。您可以使用圆规(也称为两脚规)或仅用铅笔和一些绳子来绘制一个圆。我认为我们认为圆是理所当然的,因为它太熟悉了,但它是我一些重要的数学顿悟的场所,当然,它也是数学史上的一个重要人物。
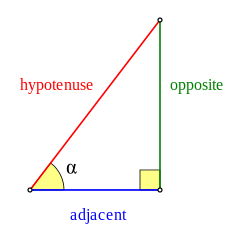
角 α 的正弦是对边(绿色标记)长度与斜边(红色标记)长度之比。来源:Dnu72, Pengo, Wikimedia(CC BY-SA 3.0)
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
三角学中的单位圆是我早期的数学顿悟之一。三角学指的是对三角形的研究(如果我们像命名大多数多边形那样命名它们,它们将被称为 trigons)。正弦、余弦、正切、正割等等函数都指的是直角三角形边长的比率。如果角 α 小于 90 度,您可以通过绘制一个角等于 α 的直角三角形,并取邻边与斜边长度的比率来找到其正弦。如果您的角度大于 90 度,您仍然可以计算角度的正弦,但您必须基于一个角度为 180-α 而不是 α 的三角形。
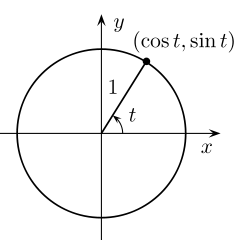
三角学中使用的单位圆。角 t 的正弦是斜边与单位圆相交点的 y 坐标,t 的余弦是 x 坐标。来源:Gustavb Wikimedia(CC BY-SA 3.0)
通过将所有直角三角形的斜边设置为等于 1 并将它们放置在一个圆内,可以大大简化理解不同三角函数和不同类型角度之间的所有关系。现在,当您将边长除以斜边长度时,您不必担心任何事情,因为斜边是 1 个单位长。您可以直接从图中读取正弦值!在挣扎了几周试图记住三角形中哪个三角函数是哪个角度之后,学习然后内化单位圆对我来说是巨大的。我可以通过可视化一个角度沿着圆移动来看到正弦和余弦之间的关系。理解这个想法使三角学感觉不仅仅是记住一堆规则。我太害怕承诺和不适而无法纹身,但如果我考虑纹身,单位圆将在列表中排名很高。
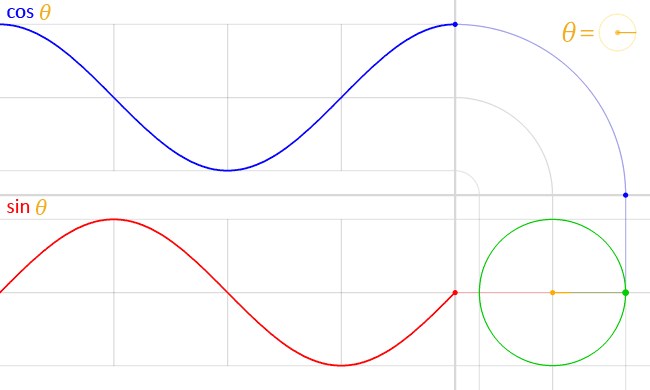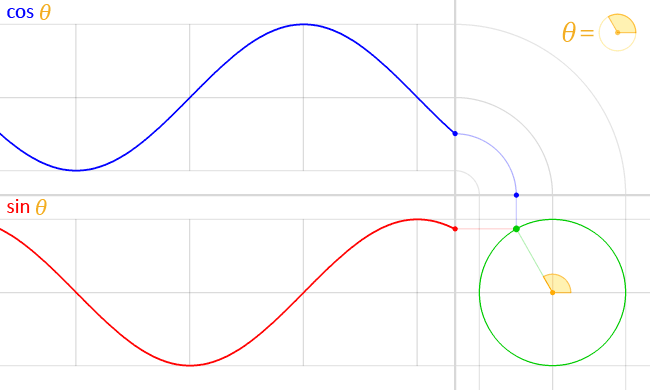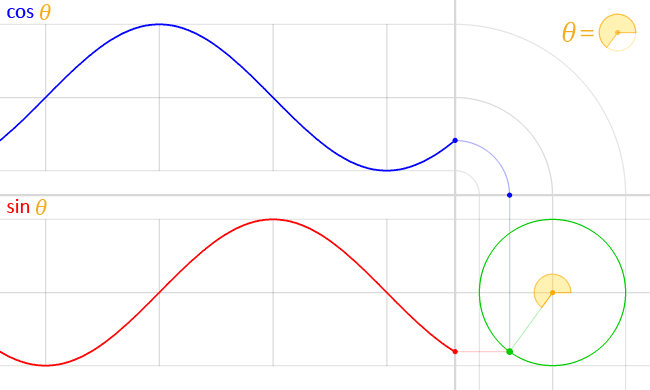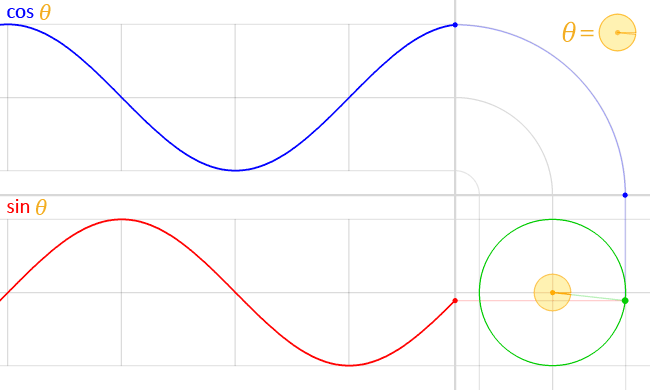
一个 gif 动画,说明了当角度围绕单位圆移动时正弦和余弦的关系。来源:LucasVB Wikimedia
然后是测量单位圆的长度,或任何圆的周长与其直径之比的问题,一个您可能听说过的称为 π 的小常数。正如 Dave Richeson 在《我最喜欢的定理》播客的一集中描述的那样,为了弄清楚圆的外部有多长,我们首先必须弄清楚弯曲而不是直线段的长度的含义。许多古代文化都知道 π 的良好近似值,但对这个数字本身的研究——获得更好的界限,确定它既不是有理数也不是代数数,以及目前对它是否是正规数的调查——一直是数学中漫长而重要的旅程。
但您可以在圆周率日阅读更多关于圆和 π 的信息,所以我们将继续前进。我在本文中将单位圆介绍为一维球体,部分原因是因为它听起来很花哨和正式,部分原因是因为理解圆的维度是我又一个数学顿悟时刻。
如果我们称圆为一维球体,那么我们有理由以类似的方式定义更高维度的球体。因此,如果 S1 是满足方程 x2+y2=1 的点集 (x,y),那么二维球体 S2 就是三维空间中满足方程 x2+y2+z2=1 的点集 (x,y,z)。(这是我们最习惯称之为球体的形状。)三维球体 S3 是四维空间中满足方程 w2+x2+y2+z2=1 的点集 (w,x,y,z)。您明白了。n 维球体,或 n 维球体,是 (n+1) 维空间中的点集。为什么会出现这种维度不匹配?
简而言之,因为一维球体是 1 维物体的球体。二维球体是 2 维物体的球体。但像这样思考它们并不容易。如果您问人们圆的维度是多少,我敢打赌他们中的大多数人会说是二维,我认为有两个原因。
首先,我们在术语“圆”的使用上非常草率。在上面的定义中,圆只是正好距离 (0,0) 1 个单位的点,而不是 (0,0) 1 个单位以内的所有点。当我还是个孩子的时候,我学到了,您可能也学到了,圆的面积是 πr2,其中 r 是圆的半径。该公式实际上适用于圆盘的面积,即原点和圆之间的所有点,满足 x2+y2≤1 的所有点,它是一个二维物体。有时我们使用“圆”这个词来同时表示这个空间的边界和内部,然后当我们想要仅对其中一个空间使用该术语时,我们就会产生混淆。
但即使我们设法区分了圆和圆盘,也很难将圆视为一维的。我认为真正理解为什么圆是一维空间而不是二维空间,对我来说是一个重要的概念突破,当我最终理解它时。很容易看出为什么圆感觉是二维的。我用两个坐标x 和 y 将其描述为二维空间的子集。但是,如果我将其描述为三维空间中的点,使得 x2+y2=1 且 z=0 呢?该方程描述的圆与我们放在二维空间中的圆形状完全相同,但现在它是三维空间的子集。我认为我的重大突破是理解,在数学上,我们希望维度反映形状的内在属性,而不是形状所处空间的属性。
数学家经常通过调用蚂蚁生活在表面上的想法或思考放大表面来描述维度。如果生活在形状上的蚂蚁认为它看起来像一条线,或者如果充分放大的版本看起来像线段,则该形状是一维的。如果看起来像一条线对您来说太含糊不清,也许您更喜欢考虑限制在圆上的蚂蚁可以移动的方式。生活在圆上的蚂蚁可以向前或向后走,但仅此而已。蚂蚁可以行进的方向轴只有一个。当我们在地球表面旅行时(我们可以挖掘或跳跃一点,但我们或多或少被限制在二维球体上),我们可以在南北方向和东西方向的组合中旅行,所以我们有两个轴来描述我们可以移动的方式。
圆可能是维度不完全明显的数学空间的最简单示例,因此,对我来说,思考它并真正内化其一维性是开始从对象本身的角度,而不是环境空间的角度来数学地思考维度的关键。一旦您掌握了这一点,您就可以理解为什么二维球体(沙滩球的表皮的形状)从根本上来说是一个二维空间。然后您可以开始思考更复杂的表面以及二维性如何在世界中排列自身的所有不同方式。我们呢?我们这些三维生物,在宏伟的事物计划中只是微不足道的尘埃,感觉我们生活在一个无尽的三维空间中,但它可能会自身循环吗?我们的宇宙可能具有哪些更大的结构?我们如何才能知道?突然之间,您正在思考庞加莱猜想,这是本世纪迄今为止最重要的数学突破。而这一切都始于一个圆!对于一个字面上代表我们数字系统中“虚无”概念的符号来说,这还不错。
阅读更多关于我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的线 具有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫链环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 法国国家铁路度量 曼德勃罗集 法图煎饼 伪球面 杜瓦迪兔子 庞加莱同调球 柯瓦列夫斯卡娅陀螺 一个 6 孔环面 实射影平面