本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
考虑一下正方形。
.png?w=350)
来源:伊芙琳·兰姆
多么好的一个正方形。如此稳固和可预测。就那样坐在 x 轴上,管着它自己的事,完全没有意识到我们即将要对它施加的奇怪数学。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
那种奇怪的数学始于一种叫做字典序的东西。起初它看起来相当无害。我们将声明单位正方形中的某些点“小于”其他点,就像数字 1 小于数字 2 一样。在这种情况下,正方形中的点 (a,b) 小于点 (c,d),如果满足以下两个条件之一:要么第一个坐标 a 小于 c,要么 a 等于 c 且第二个坐标 b 小于 d。(我们称之为字典序,因为它类似于我们按字母顺序排列单词的方式。)
如果我们选择单位正方形中的两个点,我们总是可以声明其中一个小于另一个。例如,点 (1/3,1/2) 小于 (1/2,1/3),因为它的 x 值 (1/3) 小于 1/2。它也小于 (1/3,3/4),因为它们的 x 值相同,而它的 y 值较小。到目前为止,一切都很好。
现在事情将变得奇怪:我们将使用该排序在单位正方形上定义开集。在拓扑学中,开集是命运。它们构成了我们理解数学空间的基础。例如,处理数轴的常用方法是依赖于使用区间形式的开集,例如包含大于 0 且小于 1 的所有内容的跨度 (0,1)。对于具有字典序的单位正方形,我们还通过查看严格介于两个端点之间的所有内容来构建开集。
在字典序中,有两种基本类型的开集。当两个端点具有相同的 x 坐标时,就会出现普通的香草型开集。例如,(1/3,1/2) 和 (1/3,3/4)。在这种情况下,开集只是两个点之间的垂直区间。
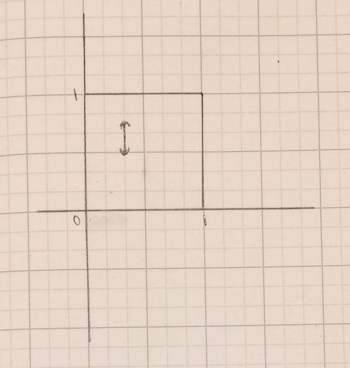
来源:伊芙琳·兰姆
如果它们具有不同的 x 坐标,事情会变得更加令人兴奋。端点为 (1/3,1/2) 和 (1/2,1/3) 的开集具有两个点之间的垂直带。
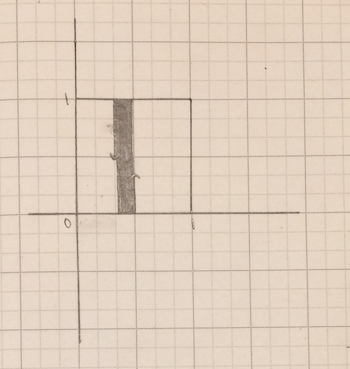
来源:伊芙琳·兰姆
一旦我们“超出”正方形的顶部或底部,开集就会自动获得一个垂直带。它可能非常窄,但它将永远存在。这是因为在区间 [0,1] 中没有“下一个”实数。没有大于 1/3 的最小数可以让我们直接到达顶部,然后环绕到底部并重新开始。
这导致了一些怪异之处:你可以有长度小于一个单位的开集,也可以有无限长的开集,但你不能有介于两者之间的任何东西。没有长度为三个单位的开集。所有保持在一条垂直线上的开集在长度上都是有限的,但那些环绕的开集是无限长的。这相当不方便地意味着在这个空间中“你无法从这里到达那里”。(数学家会说这个空间不是道路连通的。)如果你想从点 (1/3,1/2) 走到 (1/2,1/3),你找不到一条路径可以让你从一个点到达另一个点。从这种排序和我们从中获得的拓扑的角度来看,它们彼此之间无限遥远。(数学家会说这个空间不是道路连通的。)
当我第一次听说具有字典序的单位正方形时,它让我想起了长线,这是一个我在二月份写过的空间。描述长线的俏皮方式是说它就像普通的数轴,但更长。描述它的更复杂的方式是通过将其与普通的数轴进行比较。普通的数轴可以被认为每个整数都具有一个单位长度。长线对于每个实数都具有一个单位长度。(至少如果你相信连续统假设的话。但你必须阅读这篇文章才能深入了解。)
即使它们的呈现方式非常不同,我也花了一段时间才说服自己,长线和具有字典序的单位正方形实际上不是穿着不同外衣的同一个空间。(当我翻阅我的《拓扑学反例》副本时,当我看到它们有很多共同的性质时,我感到很欣慰。)
在某种意义上,这两个空间都是无限多(实际上是不可数多个)单位区间的集合体。但它们之间存在一些差异。其中之一是道路连通性。我们刚刚看到具有字典序的单位正方形不是道路连通的,但长线是。长线的定义免费为你提供了一个排序,因此你不会遇到使单位正方形无法道路连通的相同问题。
如果这听起来很奇怪,那是因为它确实很奇怪。排序并不便宜。或者至少良序,你可以总是说出一个集合中“最小”的数字,并不便宜。我们擅长良序化像全体数字这样的小型无限集合,但我们从未找到一种方法来良序化像实数这样无限的集合。我们可以说 1/3 小于 1/2,但我们不能说大于 1/3 的最小数字是什么。但是当我们定义长线时,我们开始使用一个有序的不可数集合。这方便得多,并且意味着我们始终知道接下来会发生什么。因此,对于长线上的任意两点,我们可以计算出它们之间的距离,并且我们可以通过遍历有限的,尽管可能非常长的距离来到达两点之间。
如果思考单位正方形和长线上的字典序的奥秘还没有让你精疲力尽,那么思考一下如果你将具有字典序的单位正方形从闭单位正方形更改为开单位正方形,通过决定顶部、底部和两侧不再是空间的一部分,单位正方形会发生什么变化,这很有趣。它会变得更奇怪还是更不奇怪?
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的线 带有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫链环的连通和 博罗梅安环 谢尔宾斯基三角形
