本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在我的上一篇文章中,我写了如何将“展开”一个矩形台球桌变成环面,或者说是一个百吉饼或甜甜圈的表面。这篇文章是阅读本文的良好背景。矩形是展开多边形以获得表面的一个简单例子。它的四个角拼合在一起,总共达到完美的 360°,这使得它几乎太简单了。我想看看我是否真的理解了如何通过尝试另一个例子来展开台球桌。
当玛丽安·米尔扎哈尼在 2014 年赢得菲尔兹奖时,我惊讶地发现,关于她和另一位菲尔兹奖得主阿图尔·阿维拉的作品的视频中都出现了五边形中的台球(在 Quanta 关于米尔扎哈尼的视频中1 分 20 秒处和关于阿维拉的视频中1 分 00 秒处)。所以几天前,我决定展开一个五边形台球桌,看看它会形成什么表面。
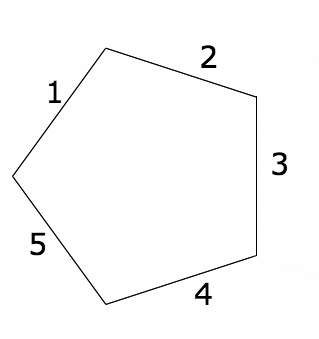
来源:伊芙琳·兰姆
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
我们可以展开五边形的一种方法是沿着五边形上的轨迹,就像我们对矩形所做的那样。但这真的没有必要。沿着一个点的轨迹绕圈走的重要之处在于,最终我们看到了矩形以每种可能的方式旋转和反射,从而保留了它的顶点。所以我从一个单独的五边形开始,并标记了边缘以帮助我记账。然后我沿着一条边展开它,并记录了哪些标签去了哪里。
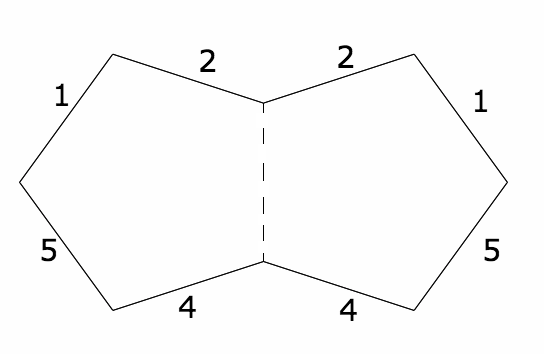
来源:伊芙琳·兰姆
然后我重复这个过程,直到我沿着每个可能的边缘都反射了它。我的作品比上面的计算机生成图像要凌乱一些。我用纸和一堆彩色笔和铅笔在纸上完成了它。它没有像米尔扎哈尼巨大的纸质涂鸦那样宏大,但它对我来说很有效。最后,我有五个双五边形的副本。(还有一点草稿。)
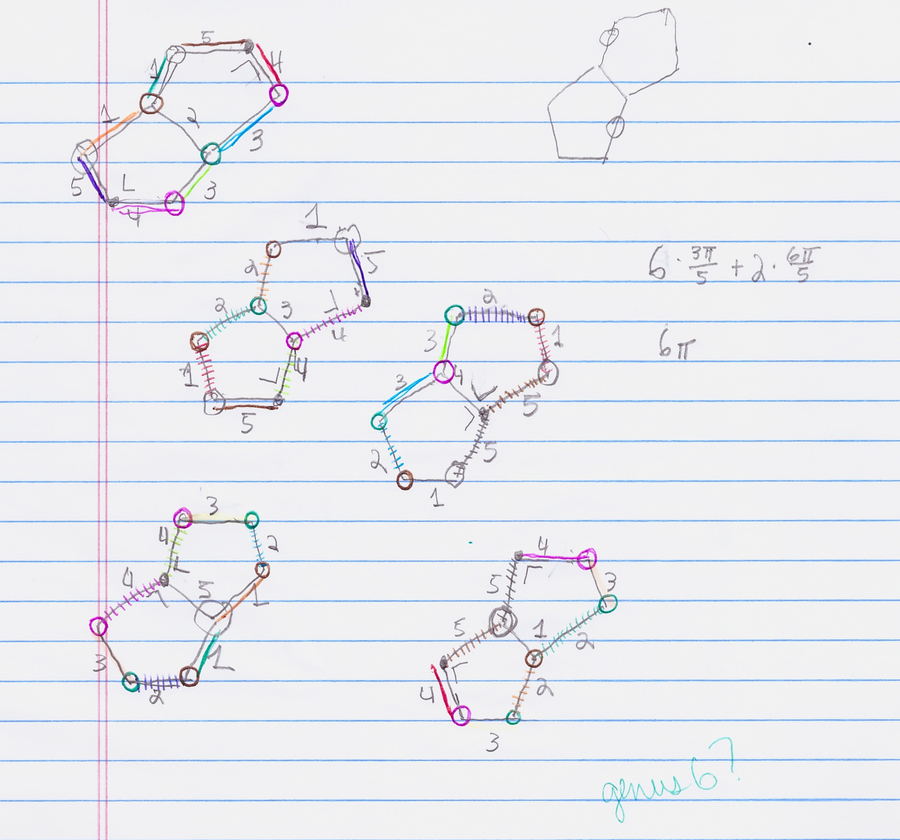
来源:伊芙琳·兰姆
将矩形转换为环面很容易可视化。将五个八边形集合与一堆标记的边缘一起,并弄清楚当您将所有边缘粘合在一起时,甜甜圈将有多少孔,这有点不太直接。
我记录了标签,并且知道应该将哪些边缘粘合在一起,但我还需要一个成分来计算我的表面中的孔数:高斯-博内定理。
高斯-博内定理是一个神奇的定理(不完全是我最喜欢的,但也很接近),它将曲面的曲率与其拓扑结构联系起来。它部分指出,多孔甜甜圈的总曲率为2π(2-2g),其中g是亏格,或表面具有的孔数。因此,只有一个孔的甜甜圈的总曲率为 0。当然,曲率有一个技术定义,但将其视为表面弯曲的程度就可以了。平坦的东西曲率为 0,像球体一样圆形的东西具有正曲率,而像马鞍形一样的东西具有负曲率。
在我们的例子中,我们展开的多边形是完全平坦的。因此它们的表面不会对总曲率产生任何贡献。但是当我们把它们粘合在一起时,我们会得到一些顶点,它们的周围角度超过 360°。曲率就在这里。当我们把矩形粘合在一起时,我们很幸运,四个直角加起来正好是 360 度。在双五边形的情况下,稍微多记一些账就可以看出,我们在表面上有 5 个奇怪的点,每个点的周围角度为 1080°(6π 弧度)。这些点有点像停车场:如果你一直绕着其中一个点转,你旋转 360° 后不会回到你开始的地方。
由于原因需要比这篇博文更长的时间来解释(你只需要相信我的话),每个特殊点周围的超额角度(即,超过 360 度或 2π 弧度的量)会影响表面的总曲率。(它带有一个负号,因为它使表面更具负曲率,像马鞍而不是球。)因为五边形是平坦的,所以所有曲率都存在于顶点处,所以我们可以使用高斯-博内定理,以及对表面有多少超额角度的计算,来计算其亏格。五个奇怪的点每个都对表面贡献了 720°(4π 弧度)的负曲率。总共为 -20π。将其代入高斯-博内定理,我们看到 2π(2-2g)=20π。我们可以消除每边的几个因子,得到 2g-2=10,因此 g=6。
当我最终使计算结果成立时,我真的很高兴。当我查阅一些台球参考文献并发现我做对了时,我更加兴奋!有关多边形中台球的更多信息,请查看这些参考文献
台球和平面,作者:戴安娜·戴维斯(Diana Davis)(面向数学背景较少的人)
台球的共形几何,作者:劳拉·德马科(Laura DeMarco)(面向数学家)
就是这样!五边形展开成一个亏格为 6 的表面,或一个六孔环面。即使一个单独的五边形看起来与像那样大的复杂表面相去甚远,但粒子在任一表面上的流动行为都是相同的。分析一个可以解释另一个表面上发生的事情。我必须承认,我看不出展开的五边形粘合在一起作为亏格为 6 的表面会是什么样子,但我无论是否可以可视化它,都能够进行分析。话又说回来,我可能不得不拿出一些布料和线,为埃莉 L 形桌子制作一个同伴,埃莉是我最喜欢的柔软而<0xC2><0xA0>有弹性的亏格为 2 的表面。
阅读更多关于我最喜欢的空间: 康托尔集 胖康托尔集 拓扑学家的正弦曲线 康托尔的漏帐篷 无限耳环 具有两个原点的直线 具有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛 沿狭缝粘合的两个环面 空集 门格海绵 四个霍普夫环的连通和 博罗梅安环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 公制 曼德勃罗集 法图的煎饼 伪球面 杜阿迪兔子 庞加莱同调球面 科瓦列夫斯卡娅陀螺