本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
配偶:你这个月最喜欢的空间是什么? 我:我还不确定。有什么建议吗? 配偶:嗯,这个月是我的生日。你可以做一个平面。 我:我应该做哪一个? 配偶:哦,哦,做两个沿狭缝粘合在一起的环面!我喜欢那个! 因此,本月最喜欢的空间献给我的好配偶。生日快乐!
我的配偶的研究领域位于几何学和动力系统的交叉点。几何学是不言自明的:形状、距离。动力系统,或动力学,是研究随时间变化的空间的学科。
我的配偶研究的系统类型之一是多边形中的台球。典型的例子是矩形中的台球,这正是实际台球游戏的玩法。数学家忽略了摩擦或球桌不规则性的影响,并以理想化的方式思考台球。不是具有质量的球,而是一个单点沿直线移动,直到撞击球桌的侧边,此时它与侧边发生完全弹性碰撞,并沿另一个方向继续前进。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和思想的具有影响力的故事的未来。
但即使那样对于数学家来说也太多了!所有这些弹跳和改变方向使得跟踪轨迹变得过于复杂,因此他们采用了一个巧妙的技巧来简化他们的问题:他们展开球桌。当球撞击侧边时,不是球被反射,而是球桌被反射,球继续不受阻碍地前进。这样,方向永远保持不变。为了了解这对于矩形是如何工作的,我们将跟随一个点周围,看看会发生什么。
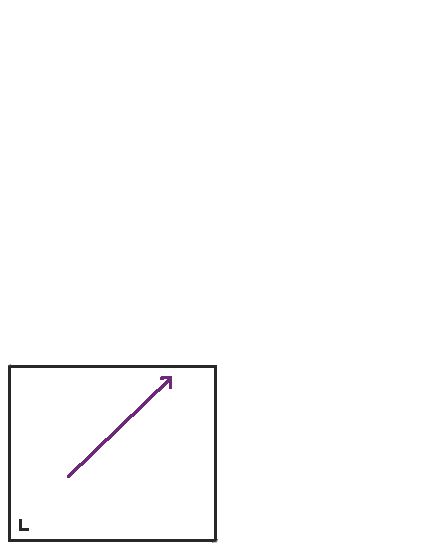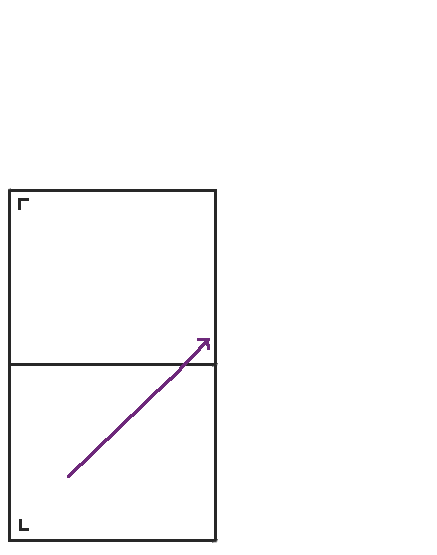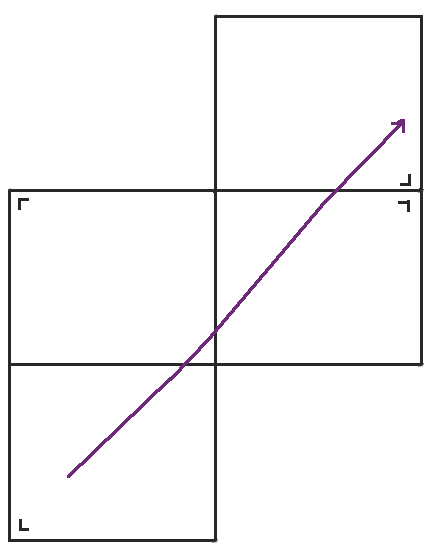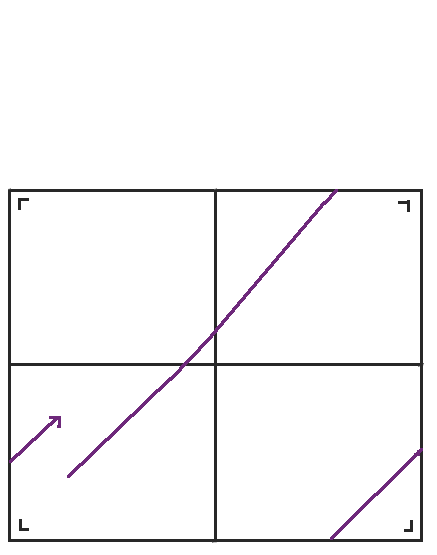
首先,我们从矩形中向东北方向移动开始。我在左下角用一个小 L 标记了矩形,以便我们可以跟踪当我们展开球桌时球桌的方向。
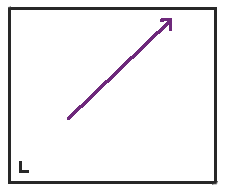
当我们到达矩形的顶部时,不是弹回,而是将球桌沿顶部反射,并且点继续前进。
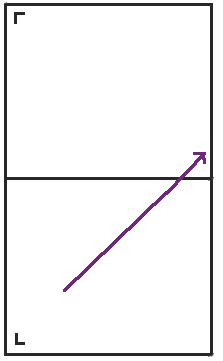
当我们到达球桌的右侧时,我们将球桌沿右侧反射并继续前进。

当我们到达那个球桌的顶部时,我们再次反射。
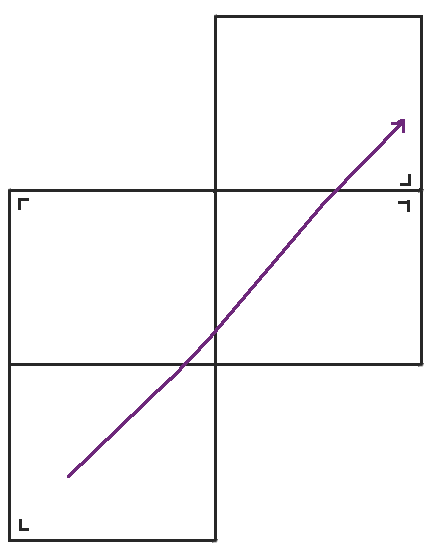
当我们到达右侧时,我们可以再次反射球桌,但是左下角的球桌与我们将要得到的球桌具有相同的方向,所以我们不妨再次跳回到左下角的球桌。当我们稍微重新排列球桌时,我们得到了我们熟悉的环面,一个顶部粘到底部,左侧粘到右侧的矩形。

这是整个过程的 gif 动画。
通过这种方式,矩形中的台球与环面上的直线流直接相关,而直线流更容易研究。西北大学数学家戴安娜·戴维斯有一篇关于数学台球的精彩的科普论文 (pdf),其中提供了更多关于多边形中的台球和曲面上的直线之间关系的信息。
我的配偶非常喜欢矩形上的台球,但那里的轨迹行为已经被很好地理解了,所以他想要更大的挑战。使曲面复杂化的最简单方法是向其添加障碍物。想象一下,某个不体谅他人的人将他们的球杆钉在了球桌上,并且球除了侧边之外还从球杆上弹开。
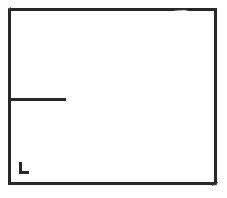
我们可以像对矩形所做的那样进行相同的展开程序来获得这张图片。
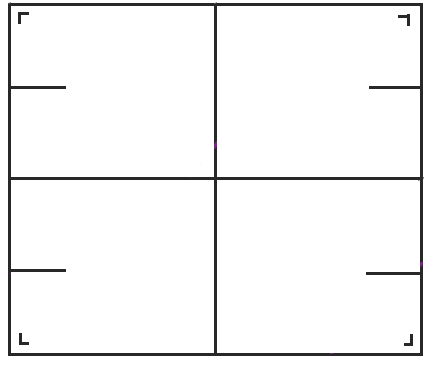
但现在我们需要小心。我们希望台球轨迹都是直线的,而不是弹跳和改变方向,因此当我们撞击障碍物时,我们需要跳到障碍物的另一个副本并沿相同的方向继续前进。这样,它变得更像一个狭缝或虫洞——你从一侧掉进去,然后从另一侧出来。
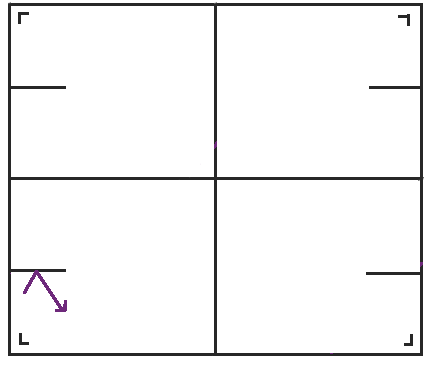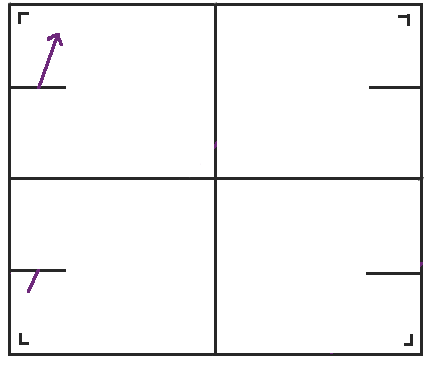
现在我们遇到了一个有趣的困境。我们可以将左右两侧粘合在一起,没有问题,但是狭缝将图形分成两个圆柱体。我已经将一个涂成蓝色,另一个涂成橙色。

在这一点上,我们可以完全重新概念化图形,以获得我的配偶非常喜欢的空间,即沿狭缝粘合在一起的两个环面。球桌上的狭缝应该粘合在一起,使每个圆柱体成为一个单色的环面,其中一侧的一部分实际上没有粘合在一起。然后你可以拖动未粘合的部分,使其更容易看到,就在环面的正中间。我已经用二维方式将其描绘为两个带有识别线绘制的矩形——你将匹配的线粘合在一起——但你也可以在三维中将其视为两个由细果冻线连接在一起的甜甜圈。(或者也许我只是饿了。)
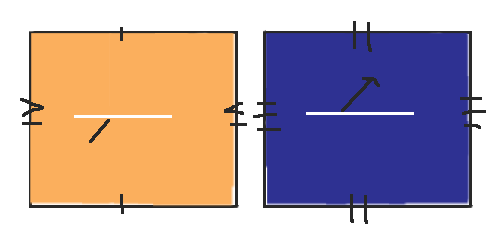
相信我,你不会想看到我尝试用 3D 绘制这个。
有趣的是,台球桌上的狭缝与环面上的狭缝是不同的狭缝!我在环面上用白色绘制了狭缝,以将其与球桌上的狭缝或障碍物区分开来。在这种情况下,当轨迹撞击一个环面上的狭缝时,它会从另一个环面上的狭缝中弹出,并沿相同的方向继续前进。再一次,狭缝就像一个虫洞,这次是在两个环面之间。
既然我已经不厌其烦地描述了这个空间,那么重点是什么?为什么有人会喜欢沿狭缝粘合的两个环面?我问了我的配偶,他说他喜欢它,因为它与环面或矩形中的台球足够不同以至于有趣,但又足够相似,以至于用于研究环面的一些技术也适用于那里。他还告诉我数学家可以为此设计出一些有趣的行。
动力系统中的一个基本问题是事物如何分布。在多边形中的台球或曲面上的流的情况下,这意味着我们试图弄清楚轨迹是否填满曲面,如果填满了,它是均匀地填满所有曲面,还是有些部分比其他部分更密集。
有两个性质相关但不完全相同,沿狭缝粘合的环面有助于阐明这两个性质。第一个是密度。如果流无限次地击中空间中的每个矩形,无论矩形有多小,则该流是密集的。第二个是均匀分布。如果流击中每个矩形的次数与其面积成正比,则该流是均匀分布的。也就是说,它一半的时间在矩形的上半部分,四分之一的时间在矩形的左下四分之一部分。
对于没有狭缝的矩形/环面,没有非均匀分布的密集流。在这空间中,这两个性质是等价的。但是对于带有障碍物的矩形,它们是不同的。根据狭缝的长度,一些轨迹可以是密集的,因此它们会击中球桌的每个部分,但在球桌的某些部分花费的时间比其他部分更多。
当我们开始谈论沿狭缝粘合在一起的两个环面时,我不断地问我的配偶一个又一个问题。他告诉我的越多,我有的问题就越多。有些答案是已知的,有些则不是。撇开我的绘画技巧不谈,我在这里展示的所有狭缝都应该正好位于矩形侧边的中间,因此你得到的两个环面,橙色的和蓝色的,大小相同。我的配偶说,如果你移动狭缝,使其位于矩形侧边的 2/3 处,行为是未知的。因此,我喜欢这个空间的另一个原因是,构造并不太困难,但我可以稍微调整一下它,就能找到即使是该领域的专家也还没有答案的问题!
阅读更多我最喜欢的空间: 康托集 胖康托集 拓扑学家的正弦曲线 康托的漏帐篷 无限耳环 具有两个原点的直线 带有两个房间的房子 法诺平面 环面 三环面 莫比乌斯带 长线 空间填充曲线 沃利斯筛
