本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点

用钩编制作的可爱克莱因四次曲线。图片版权归戴娜·泰米娜所有。经许可使用。
上周,数学家兼艺术家戴娜·泰米娜在Twitter上分享了她的最新创作。这是一个名为克莱因四次曲面的模型。它是不是很可爱?
那么它是什么呢?克莱因四次曲面是一个具有3个孔的二维物体,它有很多对称性。事实上,它拥有一个具有3个孔的曲面可能拥有的最大对称性:168个保持曲面方向的对称性,以及168个涉及将曲面由内而外翻转的对称性。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
定义克莱因四次曲线的方法有几种,泰米娜使用了一种涉及将 24 个七边形(7 边形)缝合在一起的方法。它基于七边形对双曲平面的 tiling(密铺)。好的,但这到底意味着什么呢?
很容易想象用六边形对规则的二维欧几里得平面进行密铺。我们经常看到这种情况,从浴室瓷砖到蜂巢。正六边形的每个角都是 120 度,当我们把三个六边形在一个顶点处粘合在一起时,我们得到的东西是 360 度,这非常平坦,并且恰好适合平面。

这些黄蜂喜欢用正六边形密铺平面!图片来源:Shardayy,via flickr。
如果我们使用五边形而不是六边形,我们仍然可以将三个五边形在一个点处粘合在一起,但我们最终得到的不是 360 度,而只有 324 度,因为正五边形的每个角都是 108 度。我们不能用它们密铺平面,但我们可以将它们粘合在一起,并将它们闭合成一个非常漂亮的曲面,即十二面体。
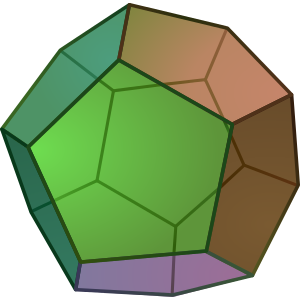
十二面体。图片来源:DTR,via Wikimedia Commons。
另一方面,如果我们使用七边形,我们得到的不是角度亏损,而是角度盈余。正七边形的每个内角略大于 128 度,所以当我们把三个七边形在一个顶点处放在一起时,我们得到的角度大于 360 度。再一次,我们不能用它们密铺欧几里得平面,但我们可以密铺一种叫做双曲平面的东西,这是一个神奇的仙境,在那里三角形的角度不必加起来等于 180 度,独角兽是真实存在的。*
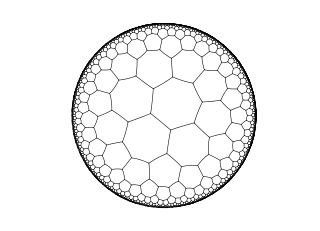
七边形对双曲平面的密铺。用“双曲眼睛”观察,这些七边形大小相同,边都是完全直的。在这张图片中,一些边缘略微弯曲,以使它们“适合”欧几里得平面。图片来源:Theon,via Wikimedia Commons。
一旦你用七边形密铺了双曲平面,你就可以以某种方式将其中 24 个粘合在一起,从而创建一个克莱因四次曲面,而这正是泰米娜所做的。你可以在她的博客上阅读更多关于她如何制作它的细节,以及从John Baez和Greg Egan那里了解一些其他理解这个曲面的方法。克莱因四次曲线无法在三维空间中完全实现,因为我们无法制作一个具有所有可能对称性的模型。曲面上的白色把手让我们了解如果泰米娜和她的钩编模型没有和我们其余的人一样被困在无聊的三维欧几里得空间中,它将如何被粘合在一起。
我一直是泰米娜作品的粉丝。据我所知,她是第一个使用钩编来创建双曲平面和其他双曲曲面模型的人。我有点知道如何钩编,并且我买了她的书《与双曲平面的钩编冒险》。当我最终有机会时,我认为研究她书中的一个项目将提高我的钩编技巧和我对双曲几何的理解。泰米娜启发了许多其他数学家创作双曲空间的钩编模型作为教学工具。我在这里写过其中一位。如果您对泰米娜的双曲钩编方法更感兴趣,请查看她的网站。
*这句话部分属实。