本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
在我们最近一期的《我最喜欢的定理》节目中,我的联合主持人凯文·努森和我与蒙特利尔大学数学教授玛蒂尔德·拉林讨论了她最喜欢的数学知识,即同余数问题。(您可以在kpknudson.com上收听该节目或阅读文字记录。)
同余数是一个正整数,它可以是边长为有理数的直角三角形的面积。例如,数字 6 是一个同余数,因为它是 3-4-5 直角三角形的面积。同余数问题是要找出哪些正整数是同余数。
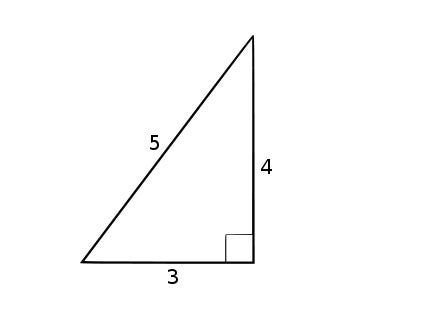
边长为 3、4 和 5 的三角形。其面积是底乘以高的一半,即 6。图片来源:Adrignola Wikimedia
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将有助于确保关于当今塑造我们世界的发现和想法的具有影响力的故事的未来。
当我听到“同余数”这个词时,我的第一个问题是,“与什么同余?”但是,即使涉及到三角形,这个名字也不是来自两个图形同余的概念,而是来自拉丁语 congruum。斐波那契使用该术语,意思是“一致”或“和谐”,来指代算术级数中平方数的差。
算术级数是连续数字之间差相同的数字序列:例如,1、3、5、7 是差为 2 的算术级数。连续平方数(1、4、9、16 等)不形成算术级数,但是如果跳过一些,您可以找到一组彼此具有这种关系的平方数。平方数 1、25 和 49 的差均为 24,因此斐波那契会将 24 称为同余数。
我的第一个问题得到了解答,我自然而然的第二个问题:同余数和同余数有什么关系?我们如何从算术级数过渡到三角形?公元 3 世纪的数学家亚历山大城的丢番图的作品中提到了同余数和同余数的早期提示,但在 10 世纪的阿拉伯手稿中,包括穆罕默德·本·阿霍钦的一份手稿中,该主题被更明确地提出,他写道,有理直角三角形研究的主要对象是寻找同余数。
我的第一个同余数的例子是 6,我的第一个同余数的例子是 24,这不是巧合。通过知道 24 是一个同余数,我们可以构造出边长为有理数且面积为 6 的三角形。
我们第一个例子中的同余数是 24,算术级数中的三个平方数是 12、52 和 72。早期的数学家认识到,当三个平方数以这种方式出现在算术级数中时,中间数的平方根(在本例中为 5)就是直角三角形的斜边。两条直角边的长度之和是最大数的平方根,而它们的长度之差是最小数的平方根。如果两个数的和为 7,差为 1,一个简单的方程组表明这两个数是 3 和 4。那么,三角形的面积就是 6,是同余数 24 的四分之一。
这个想法普遍适用。任何公差为 k 的平方数序列 x2、y2、z2 都具有以下性质:k 是斜边长度为 y,直角边长度为 a 和 b 的直角三角形面积的 4 倍,其中 a 和 b 由两个方程 a+b=z 和 a-b=x 确定。一下子看到所有这些似乎有点让人不知所措,但如果您想摆弄一些符号,验证一下并不难。
正如拉林博士告诉我们的那样,数学家们长期以来一直在尝试寻找确定给定数字是否是同余数的标准。已知一些事实:没有平方数是同余数;如果一个素数比 8 的倍数多 3,那么它就不是同余数,但它的两倍是;每个同余数都是同余数乘以有理数的平方。最后一个似乎像中了头奖,但是有理数的平方有很多,而且不容易看出给定的有理数乘以同余数是否会产生同余数。贝赫和斯维纳顿-戴尔猜想被认为是数学中最重要的未解问题之一,它的一个结果是,存在一个简单的过程来确定给定数字是否是同余数。
有关同余数、同余数和贝赫和斯维纳顿-戴尔猜想的更多信息,请查看我们与玛蒂尔德·拉林一起录制的《我最喜欢的定理》节目的节目说明,或伦纳德·尤金·迪克森的《数论史》第二卷。(关于同余数的部分从链接书的第 459 页开始。)您可以在整数序列在线百科全书中找到许多同余数的列表。
