本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
星期一,《洋葱报》报道称,“国家数学教师引入 27 个新的三角函数。” 这是一篇有趣的读物。《洋葱报》文章中的 gamsin、negtan 和 cosvnx 是虚构的,但这篇文章有一点道理:有 10 个你从未听说过的秘密三角函数,它们有令人愉快的名字,如“半正矢”和“正割外函数”。
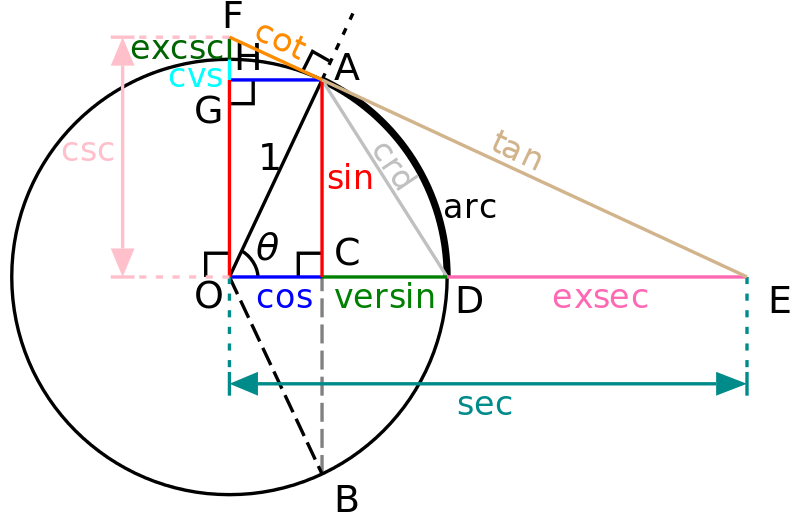
一个带有单位圆的图表,其三角函数多到你数不过来。(众所周知,你最多只能数出 8 个三角函数。) 熟悉的正弦、余弦和正切分别用红色、蓝色和棕褐色表示。余矢与余弦相邻,以绿色表示,而正割外函数在余矢的右侧,以粉红色表示。图中还显示了余余割和余余矢。未显示:余余弦、余余余弦和半-任何东西。图片来源:Limaner 和 Steven G. Johnson,通过 维基共享资源。
无论你是想用它们来折磨学生,还是在谈话中抛出它们来让自己听起来博学和/或令人讨厌,这里都是所有“丢失的三角函数”的定义
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。 通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
我在对原始历史文本进行详尽研究时发现维基百科告诉我的。
余矢:versin(θ)=1-cos(θ)
余余弦:vercosin(θ)=1+cos(θ)
余余矢:coversin(θ)=1-sin(θ)
余余余弦:covercosine(θ)=1+sin(θ)
半正矢:haversin(θ)=versin(θ)/2
半余矢:havercosin(θ)=vercosin(θ)/2
半余余矢:hacoversin(θ)=coversin(θ)/2
半余余余弦:hacovercosin(θ)=covercosin(θ)/2
正割外函数:exsec(θ)=sec(θ)-1
余割外函数:excsc(θ)=csc(θ)-1
我必须承认,当我查阅这些函数时,我有点失望。它们都只是亲爱的旧正弦和余弦的简单组合。它们为什么甚至有名字?! 在一个我可以坐在沙发上,使用在线计算器几乎瞬间找到任何角度的正弦值,精确到小数点后 100 位的地方,余矢是不必要的。 但是,这些看似多余的函数在没有计算器的世界中满足了需求。
Numberphile 最近发布了一个关于 对数表的视频,该视频解释了在黑暗的无计算器时代,人们如何使用对数来乘大数。 首先,复习一下对数。 方程 logbx=y 表示 by=x。 例如,102=100,所以 log10100=2。 关于对数的一个方便的事实是 logb(c×d)=logbc+logbd。 换句话说,对数使乘法变为加法。 如果你想使用对数表将两个数字相乘,你需要查找两个数字的对数,然后将对数相加。 然后,你将使用你的对数表找出哪个数字具有该对数,那就是你的答案。 现在听起来很麻烦,但是手动进行乘法运算比加法运算需要更多的操作。 当每个操作都需要相当长的时间(并且容易出现相当大的错误)时,一种可以将乘法转换为加法的过程是真正的节省时间的方法,并且可以帮助提高准确性。
像对数一样,秘密三角函数使计算更容易。 余矢和半正矢使用最多。 在接近角度 θ=0 时,cos(θ) 非常接近 1。 如果你在进行包含 1-cos(θ) 的计算,如果你的余弦表没有足够的有效数字,你的计算可能会被破坏。 为了说明这一点,5 度的余弦为 0.996194698,1 度的余弦为 0.999847695。 差值 cos(1°)-cos(5°) 为 0.003652997。 如果你的余弦表中有三个有效数字,由于差值中的前导零,你只能在答案中获得 1 位有效数字的精度。 精度仅为三位有效数字的表格将无法区分 0 度角和 1 度角。 在许多情况下,这无关紧要,但如果误差在计算过程中累积,则可能会成为问题。
奖励三角函数也具有永不为负的优点。 余矢的范围在 0 到 2 之间,因此如果你使用对数表与余矢相乘,你无需担心对数未针对负数定义的事实。 (它也没有为 0 定义,但这很容易处理。) 余矢和半正矢的另一个优点是它们可以让你不必平方。 一点三角魔法(又名,记住你在高中学到的无穷无尽的三角公式之一)表明 1-cos(θ)=2sin2(θ/2)。 所以半正矢只是 sin2(θ/2)。 同样,半余矢是 cos2(θ/2)。 如果你的计算涉及正弦或余弦的平方,你可以使用半正矢或半余矢表,而无需平方或开平方根。
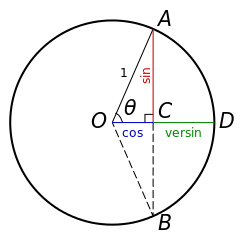
一个显示角度的正弦、余弦和余矢的图表。 图片来源:Qef 和 Steven G. Johnson,通过 维基共享资源。
余矢是一个相当明显的三角函数,定义似乎可以追溯到公元 400 年的印度。 但是,半正矢在近代历史上可能更为重要,当时它被用于导航。半正矢公式是一种非常准确的计算球体表面上两点之间距离的方法,使用两点的纬度和经度。 半正矢公式是球面余弦定律的重新表述,但是用半正矢的公式对于小角度和距离更有效。(另一方面,半正矢公式对于接近 90 度的角度效果不佳,但球面余弦定律可以很好地处理这些角度。) 半正矢公式可以产生准确的结果,而无需进行计算量大的平方和平方根运算。 早在 1984 年,《天空与望远镜》业余天文学杂志还在赞扬半正矢公式,该公式不仅对陆地导航有用,而且对天体计算也很有用。 有关半正矢公式和计算球体上距离的更多信息,请查看此人口普查局页面的存档副本或此Ask Dr. Math文章。
我没有关于列表中其他三角函数的历史的太多信息。 所有这些函数都可以使某些角度附近的计算更准确,但我不知道哪些函数常用,哪些函数是*与其他函数类似地命名但很少实际使用。 我对此感到好奇,如果有人对该主题了解更多,请告诉我!
当《洋葱报》模仿现实生活时,通常是悲剧。 但是在秘密三角函数的情况下,《洋葱报》中的一点道理并没有让我感到难过。 我们现在非常幸运,我们可以如此轻松地进行乘法、平方和开平方根运算,并且我们的计算器可以存储关于角度的正弦、余弦和正切的精确信息,但是在我们能够做到这一点之前,我们以荒谬数量的三角函数的形式找到了一个变通方法。 很容易忘记定义它们的人不是虐待狂的数学老师,他们希望人们记住奇怪的函数,没有任何理由。 这些函数实际上使计算更快,更不容易出错。 现在计算机如此强大,半正矢已经像软盘一样过时了。 但我认为我们都可以同意它应该回归,即使只是为了我昨晚睡着时想出的“真棒”笑话:半正矢? 我甚至不认识她!
*我想在这里稍微跑题到数学前缀的世界,但这可能不适合所有人。 已警告你。
在秘密三角函数表中,“半”显然意味着一半; 例如,半正矢的值是余矢值的一半。“余”意味着取相同的函数,但使用余角。 (余角加起来为 90 度。在直角三角形中,两个非直角是互余角。) 例如,一个角的余弦也是其余角的正弦。 同样,余余矢是余角的余矢,正如你在帖子顶部的图表中红色正弦之一上方的浅蓝色中看到的那样。
让我有点困惑的一个奖励三角函数是余余弦。 如果该定义中的“余”表示余角,那么余余弦将与余余矢相同,但事实并非如此。 相反,余余弦是补角(补角加起来为 180 度)的余矢,而不是余角的余矢。 除了定义为 1-cos(θ) 和 1+cos(θ) 之外,余矢和余余弦也可以定义为 versin(θ)=2sin2(θ/2) 和 vercos(θ)=2cos2(θ/2)。 就余矢而言,我相信涉及 cos(θ) 的定义比涉及正弦平方的定义更古老。 我猜余余弦是一个后来的术语,是使用余弦代替正弦平方定义的余矢的类比。 如果你是三角学历史爱好者,并且有更多信息,请告诉我! 无论如何,超级秘密奖励三角函数表是一个有趣的练习,可以弄清楚前缀的含义。