本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
我见过的最巧妙的纸牌魔术不是由魔术师表演的,而是一位数学教授表演的。
一位助教(我们称他为尼克),充当魔术师的助手,招募了五名学生参与者。每个学生从一副 52 张的纸牌中选一张,然后面朝上但汤姆教授看不到地交还给尼克。尼克将这四张牌放在汤姆面前。令我们惊讶的是,汤姆立即认出了缺少的第五张牌。
教授在课结束时揭示了诀窍。但是当我兴奋地回到宿舍时,我的室友本杰明拒绝让我解释它;他必须自己弄清楚。他喃喃自语地走回自己的房间,幸福地没有意识到在 24 小时内,这个谜题将证明对他的尊严是灾难性的。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻工作 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
纸牌魔术通常依赖于欺骗或手法,但这一个完全是关于数学的。理论上,这是大学水平的数学,但它归结为我们所有人五岁时都学到的东西:计数。
虽然这个魔术旨在突出魔术师,但稍微数一下就会发现助手才是真正的明星。毕竟,尼克不仅仅是一个纸牌管家,而是一个合作者:他可以选择四张牌的顺序,向汤姆传达信息。不仅如此,他还可以选择展示五张牌中的哪四张。因此,让我们计算一下可能性:有五种方法可以选择一张秘密卡;然后,他展示的第一张牌有四个剩余的选择,下一张牌有三个选择,依此类推。这给了尼克任何五张牌的 5 x 4 x 3 x 2 x 1 = 120 种选择。

图片来源:杰西·杜尼茨
因此,艰苦的工作在于尼克,他必须战略性地选择这 120 个选项之一;汤姆只需解释他所展示的内容。这种协作安排比读心术容易得多,但说起来容易做起来难。根据“簿记员规则”(计数原则都有很好的名字),有 260 万种可能的五张牌组合。不知何故,尼克必须能够瞥一眼这些牌中的任何一张,并挑选四张牌向汤姆发送一条编码信息,告诉他第五张牌的花色和点数。尼克如何让纸牌说话?
在看过魔术后的晚上,我和一个同学在做我们的计数作业(是的,真的),这时本杰明出现在厨房里。他用他标志性的动画风格,喋喋不休地说他已经弄清楚尼克可以选择展示哪些牌,甚至为尼克设计了一个与汤姆交流的系统。“但我还没有完全弄清楚——我还有一个信息无法弄清楚如何编码!”
当我们交谈时,本杰明靠在墙上,墙上有一个大的方形垃圾桶。他逐渐沿着墙下滑,直到他放在背后的双手抓住垃圾桶的边缘。
本杰明弄清楚的是一个核心的计数原则,称为鸽笼原理。(告诉过你它们的名字很好听。)想象一个有九个鸽笼的鸽舍。如果有十只鸽子试图在里面休息,那么至少有一个笼子里有不止一只鸽子是数学上的必然。

十只鸽子太多了——肯定有一个鸽笼里有两只鸽子! 图片来源: 维基百科(CC BY-SA 3.0)
虽然看似显而易见,但鸽笼原理导致许多非显而易见的结论。例如,我们知道有四种花色的纸牌。不可避免的是,当汤姆的观众抽出五张牌时,其中两张必须是同一花色。

应用于扑克牌花色的鸽笼原理:花色是鸽笼,纸牌是鸽子。只有四种花色,因此即使四张牌的花色不同,第五张牌也必须与其中一张花色相同。图片来源:杰西·杜尼茨
应用于扑克牌花色的鸽笼原理:花色是鸽笼,纸牌是鸽子。只有四种花色,因此即使四张牌的花色不同,第五张牌也必须与其中一张花色相同。
这表明尼克可以轻松地传达隐藏牌的花色。假设五张牌包括 J♡ 和 K♡。尼克可以将 J♡ 作为隐藏牌,并将 K♡ 作为四张牌代码中的第一张,告诉汤姆秘密牌也是红桃。
但仍然缺少一个关键部分。一旦尼克拿出第一张牌,他就只剩下三张牌了。有六种排列三张牌的方法——但汤姆必须在花色中的所有十三张牌之间做出选择。根据相同的鸽笼原理,六种纸牌排列方式无法唯一地编码十三种可能性;某些排列方式必须是模棱两可的!如何将点数也塞入展示的纸牌中?
本杰明已经弄清楚了这一切。他甚至有一个基于计数的证明,证明尼克可以将他的信息有效载荷增加一倍:由于至少有两张牌花色相同,尼克可以选择展示哪一张。这给了他两倍的选择,对于第一张牌的每种可能选择,有六个选择。
但这仍然只有尼克可以发送的十二条可能的消息。但实际上,十二个刚刚好——尼克选择的花色中的一张牌将在汤姆面前面朝上!这让汤姆的猜测只有十二种可能性。尼克拥有足够的信息携带能力。
但是在这里,本杰明卡住了。说必须能够传达必要的信息是一回事;做到这一点是另一回事。本杰明只是无法弄清楚如何将这些见解转化为实际代码。
为了使这项工作起作用,我们需要一个圆圈——特别是这一个
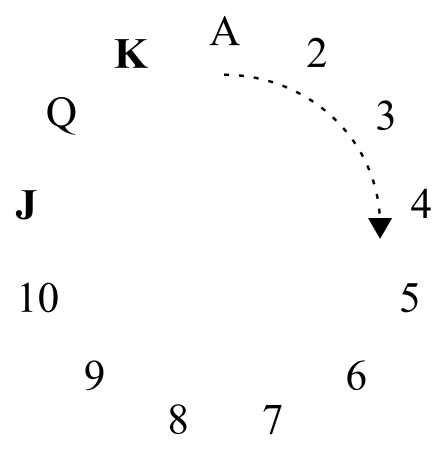
图片来源:杰西·杜尼茨
这个圆圈的有趣之处在于,尼克始终可以确保隐藏的牌与第一张显示的牌最多相差顺时针六步。假设牌组由下面显示的五张牌组成(J♡、Q♧、9♢、Q♤ 和 K♡)。尼克必须选择先显示 J♡ 或 K♡。如果他选择 K♡,那么 J♡ 在圆上顺时针跳跃 11 步。但是,如果他显示 J♡,那么只需两步即可到达 K♡!通过战略性的选择,尼克可以给魔术师一个起始点,使真实值仅在顺时针方向的几步之内。
五张牌的示例。助手应该向魔术师展示前四张,告诉他最后一张是 K♡。© Chris Aguilar,LGPL 3.0。

五张牌的示例。助手应该向魔术师展示前四张,告诉他最后一张是 K♡。图片来源:Chris Aguilar LGPL 3.0
剩下的就是让尼克告诉汤姆 1 到 6 之间的跳跃次数。他们通过预先商定牌组中所有纸牌的顺序来实现这一点。一种明智的选择是借鉴桥牌,其中花色按梅花、方块、红桃和黑桃(从低到高)排序,并且同一花色中的点数按二到 A 的顺序排序。在我们的示例中,9♢ 将“大于”Q♧,但小于 Q♤。使用此顺序,尼克和汤姆建立了一个代码,将纸牌序列转换为数字:小/中/大表示 1,小/大/中表示 2,依此类推。
接下来是用于将纸牌序列转换为圆上步数的完整表格。请访问此交互式页面,尝试亲自解码助手的消息。
纸牌顺序 | 含义 |
小、中、大 | 1 |
小、大、中 | 2 |
中、小、大 | 3 |
中、大、小 | 4 |
大、小、中 | 5 |
大、中、小 | 6 |
在我们的示例中,尼克将向魔术师展示上面显示的前四张牌(J♡、Q♧、Q♤ 和 9♢)。第一张牌告诉汤姆秘密花色是红桃。因为剩余的纸牌按小/大/中的顺序排列,所以他知道秘密值是 J♡ 顺时针方向的两步。仅凭这四张牌,汤姆就可以正确猜出 K♡。
可悲的是,本杰明从未达到圆圈魔术的程度。当他悬在垃圾桶上方时,他突然受到启发,然后大喊一声“哦!”并举起了双臂。
他忽略考虑的是,他所有的重量都压在了那双胳膊上。瞬间,他的身体塌陷到垃圾桶里,胳膊和腿像倒立的乌龟一样摇摆。他来回摇晃,但无济于事:他被困住了。
当然,我的第一反应是歇斯底里地大笑并拍了一张照片。
本杰明被困在垃圾桶里时表现得很好。他发誓说他没有穿裤子。图片来源:杰西·杜尼茨
我赶紧冲过去想帮他一把,但我喘得太厉害了,结果只是把自己弄得摔倒在地,在地上打滚大笑。最后,我那个不那么没用的作业伙伴出手了。她把那可怜的人类乌龟翻了过来,并把罐子从本杰明的屁股上拔了下来,让他得以溜走舔舐伤口。
在数学中,计数能让你走得相当远。你只需要它就可以弄清楚伦敦是否有两个人头上的头发数量相同(确实有),或者在扑克牌中拿到葫芦的概率。并且冒着听起来像伯爵的风险,这种计数不仅可以提供信息,而且令人愉快(啊-哈-哈-哈!)。
自从我上完那门课后,讲师们显然已经从讲座中删除了这个演示。毫无疑问,他们听说了他们的数学游戏给大学其他地方带来的危险。我想你必须小心计数。如果你不小心,它真的会咬你的屁股。
