本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
大众科学和数学作家马丁·加德纳(1914-2010)被认为创作了 101 本非小说类书籍和一些小说,他本应在 10 月 21 日迎来 101 岁生日。在马丁在《大众科学》的 数学游戏 专栏中 25 年期间提出的无数数学问题中,有相当多的问题引发的问题多于答案,这实际上是一件好事。
数学游戏 品牌的影响力以及对娱乐数学重要性的认可在今天仍然存在,马丁的读者现在跨越了几代人。他的铁杆粉丝继续每两年在亚特兰大举办仅限邀请的“加德纳聚会”,任何人(任何地方)都可以在每年 10 月左右参加或主办头脑庆典。最重要的是,人们不断通过为他的难题提供实质性的新解决方案以及对旧情节的新转折来推动极限。
下面,我们回顾一下一些直观的二维解剖和镶嵌突破,这些突破最初让马丁的读者感到兴奋。令人高兴的是,一些结果是最近才出现的,证实了马丁的信念,即娱乐数学除了能为好奇心和创新提供自然的跳板外,还能导致真正的持续研究。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻工作 订阅。通过购买订阅,您正在帮助确保未来关于塑造我们当今世界的发现和想法的具有影响力的故事。
三角形和正方形
解剖涉及将熟悉的形状分解成有限数量的有趣的小块,而镶嵌则涉及用一些特定形状或形状的副本填充无限空间的双重概念。
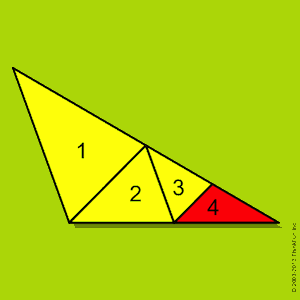
这是马丁在他 1960 年 2 月的专栏中提出的一个简单的解剖问题:“给定一个有一个钝角的三角形,是否可以将三角形切割成较小的三角形,所有三角形都是锐角的?”当然,最初的尝试,例如右图所示的尝试失败了(小三角形 4 不是锐角)。
这是他在 1981 年 4 月专栏中提出的一个更难的问题:“一个正方形可以分成最少多少个不重叠的锐角三角形?”令人惊讶的解决方案是他的原创。另一个来自 1989 年的难题至今仍未解决,归功于理查德·盖伊,他刚刚在飞往阿西尼博因山顶的直升机之旅中庆祝了他的 99 岁生日,他问是否可以用整数边长对正方形进行三角剖分,使得生成的三角形也具有整数边长?正如理查德本月在电子邮件中所说,我们仍然不知道是否可以在单位正方形的平面中找到一个到四个顶点的距离为有理数的点。
在 1958 年 11 月,马丁问一个正方形是否可以被解剖成有限数量的边长不同(整数)的小正方形,避免出现矩形子集——棋盘图案之类的在这里没有意义。自 20 世纪 30 年代以来,人们就知道这与电力网络理论有关。马丁提供的近似解决方案——一个被解剖成正方形的 32x33 矩形——那个月登上了杂志的封面(十几个此类封面中的第一个)。
找到合适的“平方数”解决方案花了 20 年时间,其中一个是边长为 112 个单位的正方形,它按要求细分为 21 个正方形。马丁给出的关于为什么沿这些方向在三维空间中不起作用的令人信服的基本论证——这意味着一个立方体不能被分解成有限数量的不相等的立方体——自从 40 年前第一次阅读它以来就一直困扰着我。由此可见,它在任何更高的维度上也行不通!
现在,让我们通过切换到镶嵌,从字面上跳出正方形的框框。在 1979 年 10 月,马丁写到了他的老朋友索尔·戈隆布在 1975 年提出的挑战:整个无限平面可以用正方形进行镶嵌吗,每个整数边长一个(1、2、3、4...)?
戈隆布的挑战一直没有被攻克,直到 吉姆·亨利和他的儿子弗雷德在 2008 年征服了它。吉姆解释说:“证明的关键是一个引理,它指出给定任何 L 形区域,都可以添加正方形来形成一个矩形。下面的动画展示了当从一个由 28x28 正方形和一个 17x17 正方形形成的 L 形开始时,这是如何完成的。”(为了便于可视化,正方形被显示为扩展到 3D 立方体。)
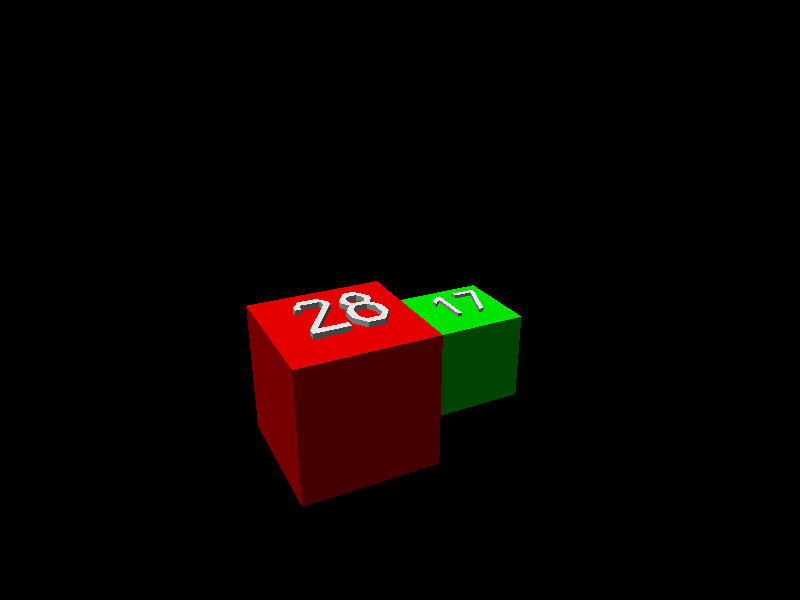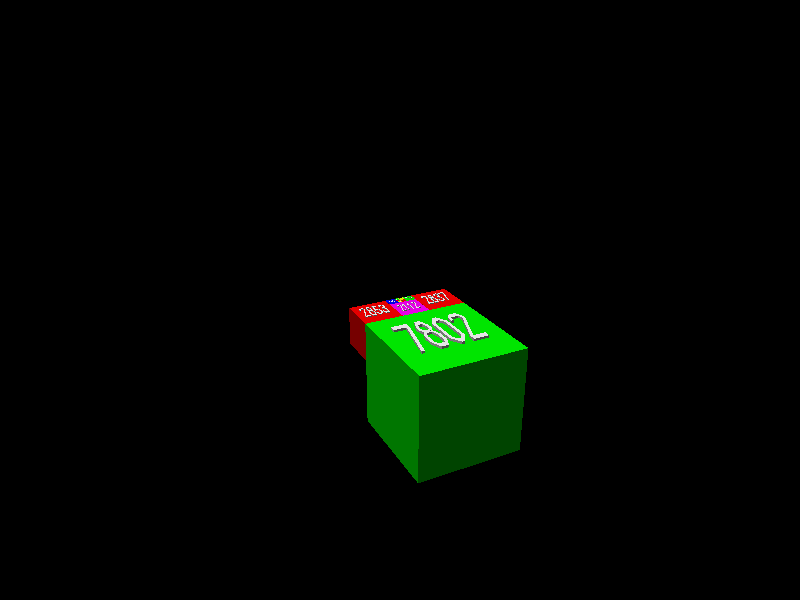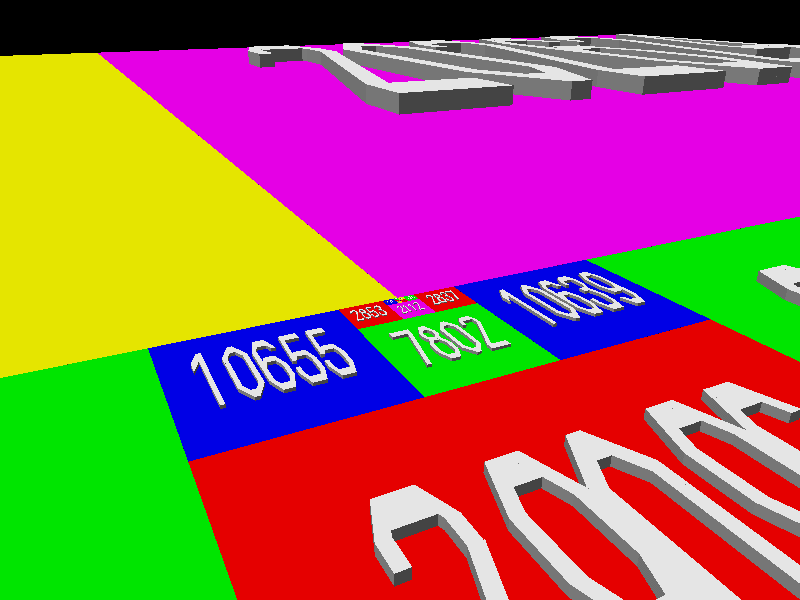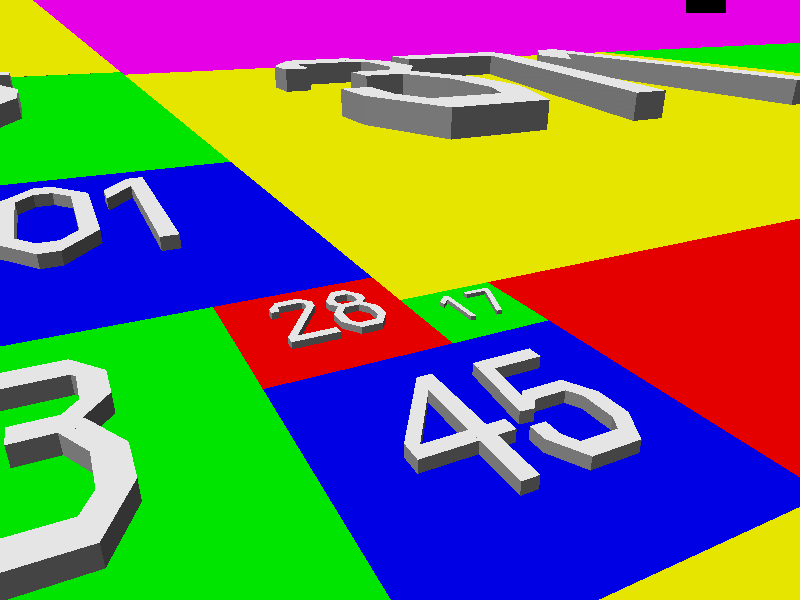
由吉姆·亨利提供。
亨利继续说道:“证明很容易从引理得出,因为一旦形成一个矩形,你可以取尚未在镶嵌中的最小正方形,并将其添加到矩形中,形成另一个 L 形(然后可以用更多的正方形扩大它,形成另一个矩形,依此类推)。”因此,每个可能的整数边长的正方形都将被生成,因为缺失的正方形将被计算在内,并且平面(在立方体之上)将被完全镶嵌。
在他们的论文末尾,作者讨论了使用三角形在类似约束条件下镶嵌平面的可能性,并提到了另一个仍然未解决的问题:“是否可以用所有有理等边三角形镶嵌平面,使得没有三角形有无限个邻居?”
在另一个狡猾的脑筋急转弯中,马丁展示了将一个三钻解剖成四个全等凸块,并要求使用五个全等凸块解剖一个正方形。
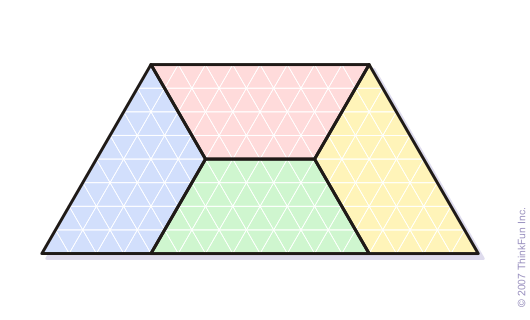
事后看来,答案是显而易见的——我们有没有提到马丁也是一位王牌魔术师,因此也是一位误导大师?然而,直到上个月(在 Liping Yuan、Carol Zamfirescu 和 Tudor Zamfirescu 的预印本“将正方形分解为五个全等的部分”中)才宣布了证明不存在其他解决方案的证明。
永远令人惊讶的五边形
超越三边形和四边形,我们来到了五边形,即五边形。 正则凸五边形不能独自镶嵌平面,因为完全对称的三角形、正方形和六边形可以,但不规则的五边形可以做到。 下面显示的各种可能性都可以在交互式Wolfram 五边形镶嵌演示项目网站上进行探索。 这个故事始于一个世纪前,当时卡尔·莱因哈特发现了五种不同类型的五边形镶嵌。 以下是其中的两个

左图:第 1 类五边形镶嵌(Tomruen/Wikimedia)。右图:第 2 类五边形镶嵌(Tomruen/Wikimedia)
五十年后,在 1968 年,理查德·克什纳发现了另外三种类型,在马丁于 1975 年 7 月的专栏中对此进行了报道后,理查德·E·詹姆斯发现了另一种类型。马丁在随后的专栏中如实地报道了这一点,圣地亚哥的中年家庭主妇玛乔丽·赖斯在她儿子的杂志副本中读到了这篇文章。尽管没有接受过数学训练,但她开始探索和整理自己的想法,并创造了自己的符号来跟踪她的发现。到 1977 年,她发现了其他人之前错过的四种全新的平面五边形镶嵌类型,从而震惊了数学界,其中两种如下所示
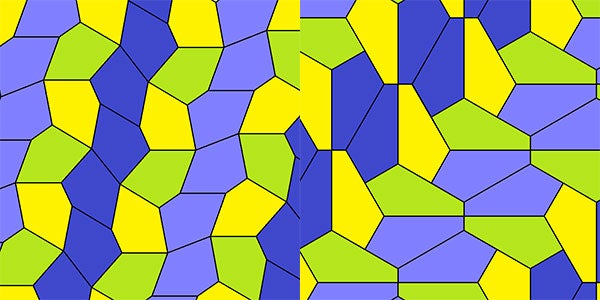
左图:第 9 类五边形镶嵌(Tomruen/Wikimedia)。右图:第 13 类五边形镶嵌(Tomruen/Wikimedia)
她的一个镶嵌——在 1995 年发现——被用作美国数学协会华盛顿特区总部的地板镶嵌,由数学家多丽丝·沙茨施耐德改编。

1985 年,罗尔夫·斯坦发现了另一种五边形镶嵌类型,使总数达到 14 种。三十年过去了,凯西·曼、詹妮弗·麦克劳德和大卫·冯·德劳都在华盛顿大学博塞尔分校于去年 7 月宣布了第 15th 种类型。以下是它的一个化身

第 15 类五边形镶嵌。(Tomruen/Wikimedia)
为了便于比较,以下是博塞尔团队提供的新面板中的所有 15 种镶嵌类型

点击放大。
是否还有其他类型的五边形镶嵌尚未被发现?如果有,可能会有多少种?詹妮弗·麦克劳德是一位美国原住民,也是她家中第一个获得学士学位的人,她指出,“关于用凸五边形镶嵌平面的方式的数量,没有已知的上限。”换句话说,可能还有数十种五边形镶嵌类型——甚至无限多种。或者也许不再有任何类型。
钉上棺材
仔细观察博塞尔五边形是很有启发意义的,它类似于一个不规则的棺材。也许麦克劳德和同事们真的已经通过发现最后一种可能的五边形镶嵌类型而钉上了棺材!
由华盛顿大学博塞尔分校提供
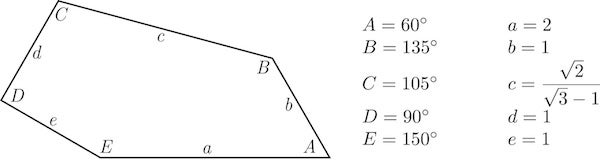
请允许我们(咳咳)研究以下角度:此形状可以通过以下方式获得:首先是一个铰接的水平 5 单位长的直棒 CDEaAB,[此处“a”是指图像中 EA 段的中点;它也指 EA 的长度],然后进行如下调整。
在右侧,将 AB 逆时针旋转 120 度,使角 A 为 60 度。在左侧,将 CD 顺时针旋转到垂直位置,然后保持角 D 为 90 度,再将 DE 顺时针旋转 30 度。 EaA 保持直线,长度为 2 个单位。最后连接端点 D 和 B:事实证明,DB 的长度为 sqrt(2)/(sqrt(3)-1),约为 1.93 个单位,角 C 和 B 分别正好为 105 度和 135 度。五边形可以分解为一个等腰三角形、一个等边三角形和一个具有“好”角的四边形。
一个孩子随意玩弄一根吸管,在几个关键位置弯曲,并且间隔适当,很容易就能得到这种五边形形状。也许,随着时间的推移,有几个人这样做过。如果是这样,他们都没有意识到自己发现的意义,一听到开饭的宣布,就把它扔到一边不再想了。谁又能说,没有哪个孩子把吸管弯成其他可以铺满无限平面的新型五边形呢?这是一种大人也可以参与的儿童游戏。
马丁最近出版的遗作绝对是适合儿童阅读的,同时也带有成年人的意味。 《注释版爱丽丝梦游仙境:150周年豪华版》 (W.W Norton出版) 是他畅销书的最终更新版本,其中包含了马丁五年前去世时留下的额外注释。