本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
数学可以帮助我们绘制真实物体。自然模式的规律性可以引导艺术家在艺术作品中使用数学概念。许多植物的叶子非常有趣和美丽,并且在它们的结构中可以找到一些数学模式。例如,螺旋芦荟是一种来自莱索托的植物。螺旋芦荟的叶子形成非常美丽的螺旋形。
有多种方法可以使用数学概念生成叶子形状。一个著名的例子是巴恩斯利蕨。英国数学家迈克尔·巴恩斯利(Michael Barnsley,生于1946年)在他的著作《分形无处不在》中描述了这个美丽的分形。他的分形类似于蕨类植物的叶子。他使用迭代函数系统方法创建了这个分形。
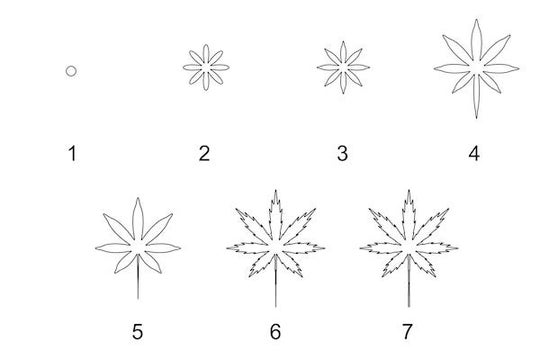
用数学公式绘制日本枫叶。致谢:Hamid Naderi Yeganeh
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
您可能会认为下面图像中的叶子是手工绘制的。但它们实际上是计算机生成的数学图形。这些形状是使用三角函数正弦和余弦生成的。在这里,我想谈谈我用来创建这些图形的方法。
当我想绘制真实物体时,我会尝试找到一个可以生成该图形的数学公式。我使用逐步过程来找到这样的公式。在该过程的每个步骤中,我尝试通过向公式添加数学表达式来增加图形与真实物体的相似性。通常,我会搜索由正弦和余弦函数生成的表达式。这两个数学函数的属性(特别是周期性、有界性和平滑性)使它们在该过程中非常有用。实际上,我需要在每个步骤中解决找到合适的数学表达式的问题。因此,某些步骤可能非常困难甚至不可能。例如,在上面的图像中,您可以看到生成类似于日本枫树叶子的数学曲线的过程。该图显示了该过程如何将一个圆转换为图形。
这些图像显示了使用上述方法创建的三个数学曲线。它们由参数方程描述
枫叶

枫叶。致谢:Hamid Naderi Yeganeh
日本枫叶
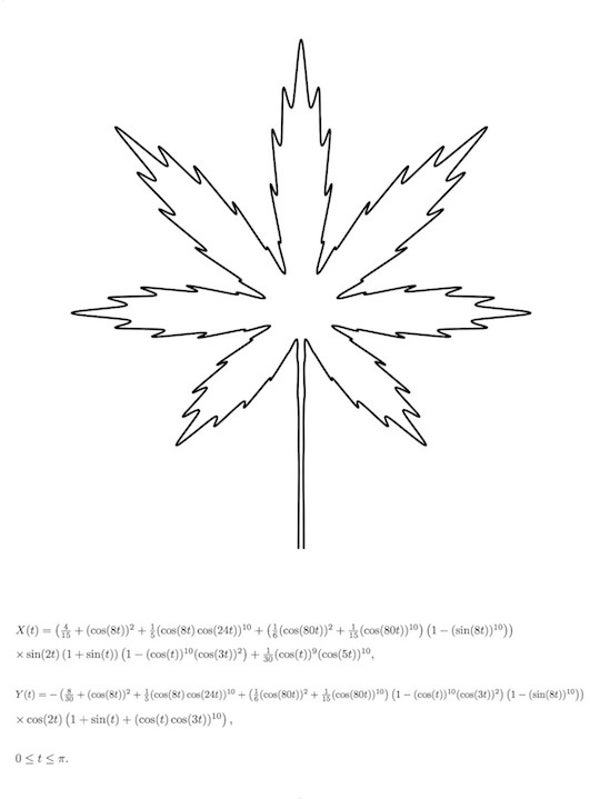
日本枫叶。致谢:Hamid Naderi Yeganeh。
橡树叶
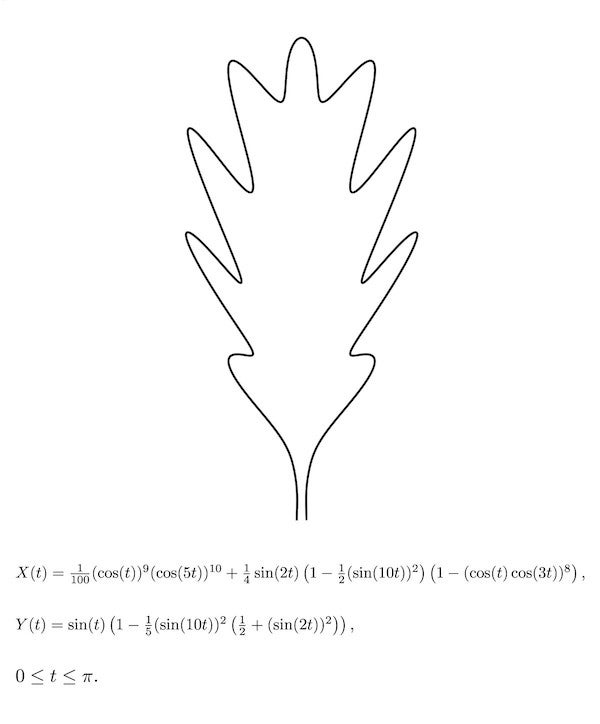
橡树叶。致谢:Hamid Naderi Yeganeh
此外,在下面您可以看到通过绘制数千个圆圈创建的两个数学图形。圆圈的半径和中心由三角函数确定。
橄榄枝
.jpg?w=600)
橄榄枝。致谢:Hamid Naderi Yeganeh
棕榈枝

棕榈枝。致谢:Hamid Naderi Yeganeh