本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
数学家以我的名字命名了一个数学对象。它被称为霍根曲面,或者,另一种说法,霍根非曲面。这个术语本意是侮辱,但我仍然感到荣幸。这是背景故事,它也关于数学领域的变革,这是所有寻求真理的努力中最纯粹的领域。
1993年,当我还是《大众科学》杂志的全职撰稿人时(不像我现在这样只是一个简陋的博主),我的老板命令我写一篇关于数学的深度报道。我抵制这项任务。在大学里,我主修英语。我只上过一门数学课,是微积分。我可以处理关于刚刚被解决的费马最后定理,或者曼德勃罗集的简短新闻报道,但一篇主要的文章会太难。我的老板坚持要我写。
我开始阅读书籍和文章,并采访著名的数学家,最终我意识到我有一个故事。一个大故事。几千年来,证明一直是数学真理——以及一般知识——的黄金标准。有什么比勾股定理更真实的呢?但是数学正在以削弱传统证明地位的方式发生变化。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的有影响力的故事。
一个问题是数学日益增长的复杂性和专业化,这使得某些所谓的证明难以验证。安德鲁·怀尔斯对费马最后定理的证明就是一个例子。当这份长达200页的密集证明首次出现时,只有少数专家有资格对其进行评估。(结果证明它有一个错误,怀尔斯最终纠正了。)
与此同时,资助机构正在向数学家施压,要求他们从事密码学和人工智能视觉等应用领域的研究。在应用数学中,动机问题从“它是真的吗?”转变为“它有效吗?”数学不再是启迪和美的源泉,不再为了自身而实践,而变成了一种工具,一种达到实际目的的手段。
数学家们越来越依赖计算机来进行艰苦的计算、模拟物体和运行实验。一些人主张接受所谓的概率证明,这种证明只有一定的可能性为真。另一些人则敦促证明应以计算机可以检查而不是容易犯错的人类可以检查的形式书写。
传统主义者对这些趋势感到痛惜,他们断言,依赖计算机的证明根本不是真正的证明。但有影响力的人物支持这些变革。其中一位是威廉·瑟斯顿,他于1982年因阐明拓扑学和几何学之间的联系而荣获菲尔兹奖——数学界的诺贝尔奖。
瑟斯顿是我文章的主要信息来源,他提倡更自由、更“直观”的数学研究、交流和教育风格,减少对传统证明的强调。他试图用计算机生成的模型来传达数学概念,包括他称之为“非结”的视频。
瑟斯顿告诉我,“数学原则上可以简化为形式证明,这种想法是不牢靠的”,这是20世纪特有的。具有讽刺意味的是,他指出,伯特兰·罗素和库尔特·哥德尔在本世纪初就证明了数学充满了逻辑矛盾。“集合论是建立在客气的谎言之上的,即使我们知道它们不是真的,我们也同意这些谎言,”瑟斯顿说。“在某些方面,数学的基础具有不真实的气息。”
“证明之死”以“非结”的剧照为插图,是1993年10月《大众科学》的封面故事。副标题是:“计算机正在改变数学家发现、证明和交流思想的方式,但在这个勇敢的新世界中,绝对的确定性还有立足之地吗?”
我的引言中写道:几千年来,数学家们一直根据他们可以通过证明——即从一组公理到无可辩驳的结论的一系列逻辑步骤——来证明的东西来衡量进步。现在,困扰现代人类思想的怀疑终于感染了数学。数学家们可能最终不得不接受许多科学家和哲学家已经承认的事实:他们的断言充其量只是暂时正确的,在被证明是错误之前才是正确的。
反弹——主要是以信件的形式,因为博客那时还没有发明——像我职业生涯中的任何一次一样强烈。数学家们指责我歪曲事实和夸大其词,尤其是在我选择的标题和封面艺术上。尽管我引用了对计算机生成证据和其他趋势的批评者的观点,但许多数学家似乎认为我是在提倡——甚至发明——这些对传统证明的挑战,而不是仅仅报道它们。
一位强烈的批评者是大卫·霍夫曼,他曾是我的文章的信息来源。霍夫曼使用计算机模型来探索极小曲面,极小曲面是由给定曲线或膜边界的尽可能小的面积或体积。我的文章包括一张霍夫曼的照片和他用计算机生成的图像。“通过在计算机上查看这些曲面的图像,我们获得了大量的直觉,”霍夫曼告诉我。我还引用了他的话,他坚持认为证明仍然是研究的最终目标。
在给编辑的信中,霍夫曼写道:“约翰·霍根的《证明之死》为了争议和耸人听闻而蔑视逻辑和准确性……我非常赞成在数学研究和交流中使用计算机图形,但是,有哪位受人尊敬的数学家愿意解释和捍卫视频证明作为传统数学方法的替代品的概念吗?”
1998年,当霍夫曼为美国数学学会通告评论我的第一本书《科学的终结》时,仍然怒不可遏。霍夫曼并非不合理地认为“证明之死”是《科学的终结》的热身。正如他所说,我那篇“十页纸的数学——我们所知的数学——已经结束的文章仅仅是对科学的全面安魂曲的一次手指练习。”
霍夫曼对《科学的终结》如此受关注感到震惊。他指责我“对数学思维有明显的反感,并且从根本上误解了数学在科学中的用途。”他用七页书评中的一大块来捍卫弦理论,反对我对弦理论的攻击。他暗示,欧洲核子研究中心的大型强子对撞机可能很快就会产生弦理论的证据——不用说,这并没有发生。
霍夫曼把我比作19世纪神话般的专利专员,他因为一切都被发明出来而辞去了工作。他写道:“在21世纪末撰写、思考和从事科学和数学的人们,将不必挖掘专利专员的半真半假的故事,来指出他们的后现代批评家的目光短浅。他们将有霍根的《终结》来发泄。”我当然希望如此。
.jpg?w=712)
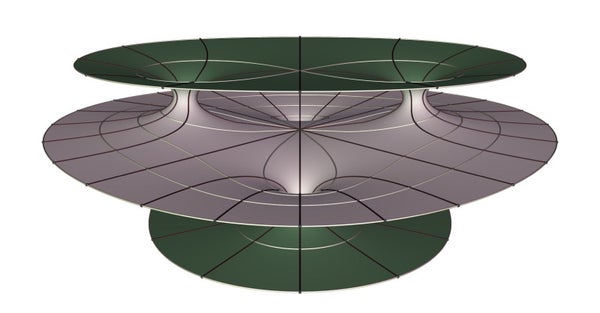
图片来源:马蒂亚斯·韦伯
与此同时,霍夫曼继续研究极小曲面。在“证明之死”发表后不久,他和赫尔曼·卡彻探索了一种新型曲面的变体。计算机建模最初表明,该对象是一个真正的极小曲面,但进一步调查似乎揭示了间隙(见上图)。霍夫曼和卡彻将该对象命名为“霍根曲面”,因为他们认为这是对计算机模型可以取代严格证明的观点的反驳。他们在论文《有限总曲率的完整嵌入极小曲面》中讨论了霍根曲面。预印本于1995年发表,1997年,该论文被收录在《数学科学百科全书》第5卷中。
我从数学家马蒂亚斯·韦伯的文章中拼凑出了这段历史,这是我最近在进行自我谷歌搜索时发现的。1998年,韦伯在《变分法与偏微分方程》杂志上发表了一篇论文《关于霍根极小非曲面》。韦伯指出,霍夫曼和卡彻创造了“霍根曲面”这个词,作为对“证明之死”的“小小报复”。韦伯补充说,其他数学家“感到好笑,但要求提供一个不存在性证明。”
我想指出这里的一个讽刺之处。霍夫曼和卡彻对我不尊重证明感到恼火,但他们并没有为他们的猜想——霍根曲面实际上是一个伪曲面——提供任何证明!韦伯提供了证明。在他的论文中,他提出了“最对称霍根曲面(或非曲面,他更喜欢这样称呼)的一个非常简单的不存在性证明。”
最近,韦伯在两篇博客文章(这里和这里)中描述了霍根非曲面并展示了它的图像。韦伯称这种非曲面为“一个简单、非平凡的例子”,它是一个表面上是极小曲面,但结果并非如此的例子。“非平凡”让我感到莫名其妙的自豪。
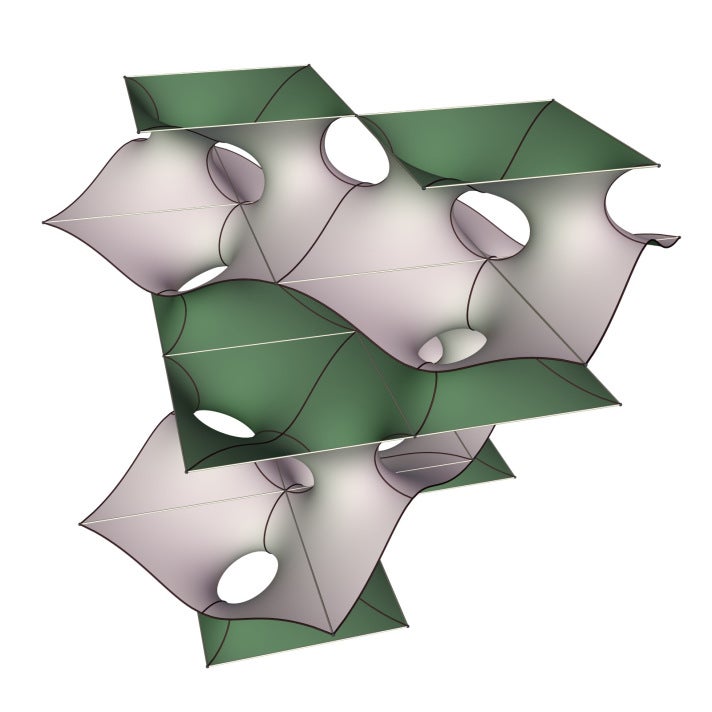
图片来源:马蒂亚斯·韦伯
韦伯已经证明了存在一个真正的极小曲面——“三重周期霍根曲面”(见上图),这也让我感到自豪。“这是霍根曲面意义重大的另一个原因,”韦伯告诉我。“这个曲面处于存在与不存在的边缘(或者说是半死不活,如果你愿意的话……),规则的细微变化就会使它倒向一边或另一边。”
在“没有对称性的嵌入极小曲面”(《微分几何杂志》,2002年)中,在Wolfram演示项目和我的维基百科页面上,也可以找到关于霍根曲面的提及。我的页面的贡献者,可能是怀有敌意的数学家,总是对“证明之死”给予过度的关注。最近有人添加了对霍根曲面的引用,强调这个名称是“讽刺性的”。
我后悔写了“证明之死”吗?当然不,就像我不后悔写《科学的终结》一样,《科学的终结》仍然引发争议。我很高兴在永恒的柏拉图式形式领域中有东西以我的名字命名,即使只是讽刺性的。我更欣慰的是,数学家们继续引用“证明之死”,即使只是为了抨击它。我的一位最激烈的批评者史蒂文·克兰茨在他的2011年出版的著作《证明就在布丁里》中指出,我的文章的主要观点“非常值得考虑”。谢谢你的赞美,史蒂夫。
韦伯在“证明之死”发表时是一名博士后,他说他“很想看到”“证明之死重装上阵”。他详细阐述道,“理想情况下,你应该和大卫·霍夫曼坐在一起,谈谈当时发生了什么,以及今天的证明、真理、新闻业和数学是什么样的,然后发表出来,不加审查。” 我给霍夫曼发邮件,问他是否愿意和我一起做一个问答,并承诺我会逐字逐句地刊登他的回答。霍根曲面的共同发现者“恭敬地”拒绝了。
数学界仍在为所谓的证明争论不休——例如,黎曼猜想和ABC猜想。韦伯认为,计算机,尤其是人工智能的进步,对传统数学构成的挑战甚至比1993年更大。“人们很容易想象专门的软件超越数学家”,成为证明的构建者,他说。“当这种情况发生时,你所思考的证明之死将被避免。我想这是一场惨胜。”
最近,我请一位数学界的朋友迈克尔·哈里斯给我写一段话,谈谈“证明之死”是如何成立的。哈里斯回复说:“碰巧的是,我最近一直在思考这个问题。 我不确定我是否能用少于1000个字来表达清楚,而且任何少于10000个字的内容都只是一连串的谜语。”
他正在组织一场公众讨论会“数学的机械化”,将于10月在纽约市的螺旋中心举行。公告指出,一些数学家已经提出“对这个行业进行彻底的反思,要求未来的证明以计算机可读的代码编写。一些数学家甚至预测,人工智能将取代人类从事数学研究,就像在许多其他活动中一样。”公告继续写道:
一个人对未来证明机械化的可能性的立场取决于一个人对数学本身的看法。数学是一种手段,一个称职的机器可以像人类一样好,甚至更好,地实现这个目的吗?如果是这样,那么这个目的是什么?为什么机器被认为比人类更可靠?或者,数学反而是一种目的本身,一种为了其内在价值而追求的人类实践?如果是这样,那么这种价值可能是什么?它能与机器分享吗?
很棒的问题。我会去那里,收集“证明之死重装上阵”的素材。我不得不做出一个让步。 霍根曲面反驳了我的证明之死论题,但方式与霍夫曼和卡彻的意图不同。数学可能正在超越我们的认知能力,机械化可能正在逼近,但人类仍在发现和证明新事物的存在。这让我很高兴。
延伸阅读:
好吧,也许证明并没有消亡 [后续文章]
身心问题 (免费在线书籍)