如果要您选择几个词语或符号来概括您的遗产,您会选择什么?约翰·卡尔·弗里德里希·高斯(Johann Carl Friedrich Gauss,1777–1855)身后留下了无数数学成就可供选择,但他最希望的是在他的墓碑上蚀刻一个“正十七边形”。这个高度对称的17边形在他认为是对数学最伟大贡献之一的证明中扮演了重要角色。在年仅18岁时,高斯利用正十七边形解决了一个困扰数学家超过2000年的经典问题。回顾这段历史,揭示了古代将形状概念化为图画的方式与现代用方程来管理形状的观点之间存在的深刻联系。
古希腊几何学
古希腊人在几何学方面非常出色,特别强调用圆规和直尺进行的作图。可以将这些作图视为具有所需几何特性的图表,仅用书写工具和两种工具创建。给定两个点,绘图圆规(不要与导航设备混淆)允许人们创建一个以任一点为圆心并穿过另一点的圆。直尺可用于在点之间绘制直线。这两种工具都没有任何标记,因此人们无法用它们测量距离或角度。
关于支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您将有助于确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
在所有可以用圆规和直尺构造的形状中,正多边形具有特殊的地位。
希腊人并非为了让数学更具挑战性而强加武断的规则。用圆规和直尺构造形状的游戏起源于公元前三世纪欧几里得的几何原本,这是有史以来最重要的教科书之一。与现代数学家一样,欧几里得着手从最少的假设中推导出所有几何学。欧几里得不是仅仅断言形状或其他几何物体的存在,而是想用最简单的成分:直线和圆,明确地构建它们。为了感受这些作图,请亲自尝试一个:找到下面从A到B线段的中点。目测是不够的;你的方法必须确定精确的中点。
首先使用圆规画一个以A为圆心并穿过B的圆。然后重复此步骤,画一个以B为圆心并穿过A的圆。这些圆将相交于两点。使用直尺连接这两点。由于构造中的对称性,这条垂直线将精确地与原始线段的中点相交。

Amanda Montañez
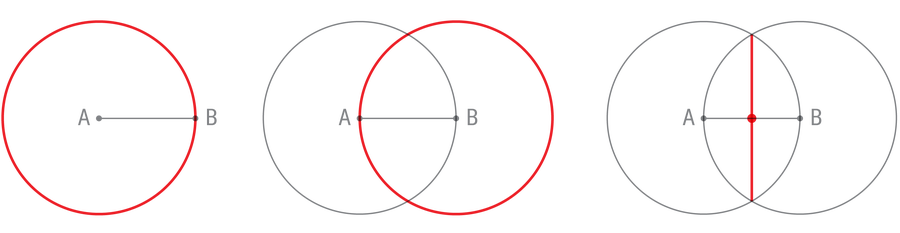
Amanda Montañez
这个练习不仅仅是平分一条线段。它在两条线之间创建了一个直角,这对于如此受限的工具集来说并非易事。通过连接更多的点,您可以制作一个等边三角形——一个边长相等且角相等三角形。
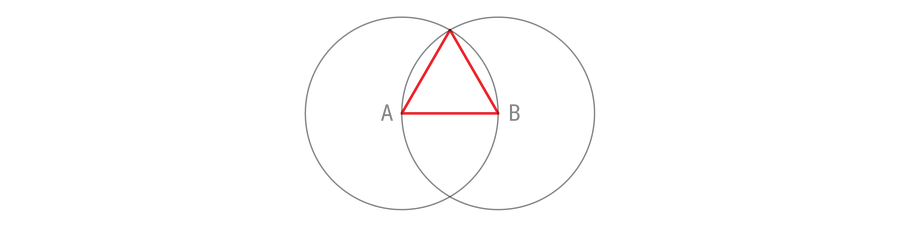
Amanda Montañez
请注意,三角形的每条边也是其中一个圆的半径。这些圆的大小相同,因此三角形的所有边都具有相同的长度。因此,等边三角形可以用圆规和直尺构造,Q.E.D. 恭喜您坚持完成了欧几里得《几何原本》第一卷中的第一个命题。还有13卷要看。
一个障碍
在所有可以用圆规和直尺构造的形状中,正多边形具有特殊的地位。多边形是由直线边组成的封闭形状,例如三角形和矩形(与圆形等曲线形状或字母E等非封闭形状相对)。正多边形具有最大的对称性,因为它们的边都具有相等的长度,并且它们的角都具有相等的度量(例如正方形和等边三角形,但与矩形和菱形不同)。用圆规和直尺构造任何旧的不规则三角形都是小菜一碟——只需在页面上散布三个点并将它们用线连接起来即可。但是构造我们完美对称的等边三角形——一个正多边形——需要一些优雅的准备工作。
欧几里得弄清楚了如何构造具有三、四或五条边的正多边形——分别是等边三角形、正方形或正五边形。他从这些核心构造中挤出了一些更多的概括;例如,一旦你在页面上有一个正多边形,一个简单的操作将产生一个新的边数是原来两倍的正多边形。
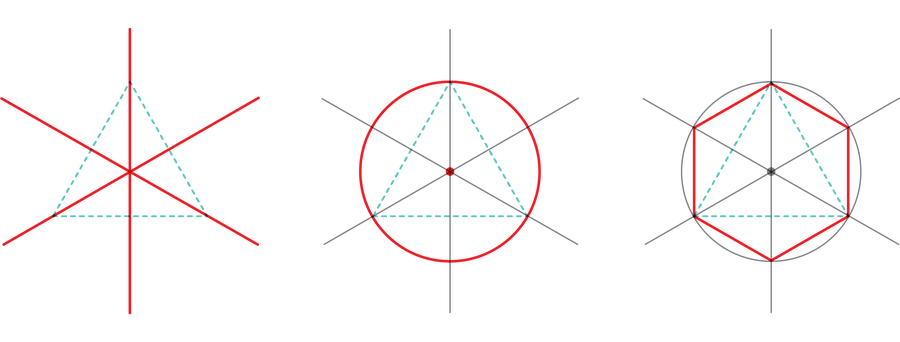
Amanda Montañez
您可以根据需要多次重复此加倍过程。这意味着三边形、四边形和五边形的正多边形可以转换为六边形、八边形和十边形的正多边形,以及十二边形、十六边形和二十边形的正多边形,等等。欧几里得还展示了如何“乘”三边形和五边形的正多边形以产生正十五边形。
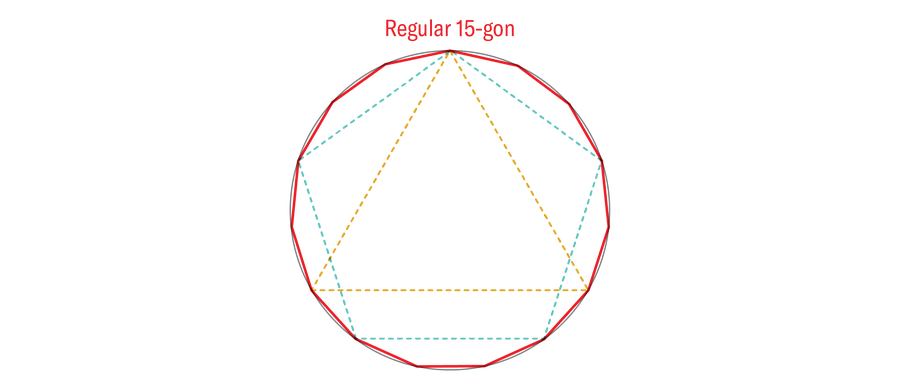
Amanda Montañez
进展到此为止停滞了。不知何故,欧几里得知道原则上可以构造一个正3072边形(一个三角形加倍10次),但他不知道如何构造正七边形(heptagon)或正十一边形(hendecagon)。需要明确的是,边数大于二的任何正多边形都存在,并且可以用更强大的工具构造。欧几里得遗留的问题是,哪些可以用圆规和直尺单独构造。这个问题在两个千年里一直没有得到解答,直到一位德国少年拿起铅笔。
18世纪的数学来救援
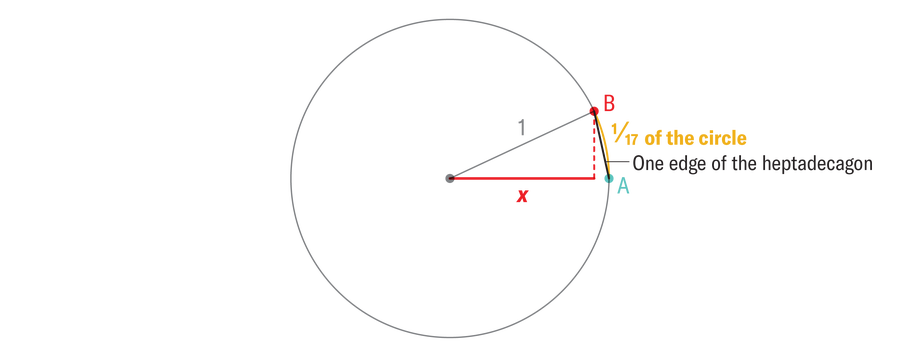
到1796年,还没有新的正多边形加入到可构造形状的行列中,但数学家们对圆规和直尺的构造有了更深入的了解。高斯知道如何将构造正多边形的问题简化为仅创建一个具有非常特定长度的线段。要构造一个17-gon,首先从一个单位圆(半径等于1)和一个圆上的点A开始,如下面的图形所示。想象一下,我们可以找到A上方红色点B,它正好在圆周的1/17处。如果我们能够从蓝色点构造红色点,我们可以围绕圆周重复该动作,并用直尺连接这些点:瞧,一个正十七边形。
但是,给定点A,我们如何绘制点B呢?请注意,如果我们能够绘制标记为x的红色线段,那么我们可以将其连接到红色点B,我们就成功了。构造正十七边形的整个问题归结为创建一个长度精确为x的线段。对于对数学好奇的人来说,x = cosine (2π⁄17)。
Amanda Montañez
我们可以使用圆规和直尺构造任意长度的线段吗?到高斯时代,数学家们已经知道这个问题的惊人答案。一个长度可构造的充要条件是它可以表示为对整数进行加法、减法、乘法、除法或平方根运算的结果。因此,一些奇怪的数字,例如99⁄5的平方根,是可构造的(99和5是整数,我们对它们应用除法和平方根),而一些更熟悉的数字,例如pi (π) 和2的立方根,则不可构造,因为永远无法仅用这五种运算来表示它们。
值得注意的是,古希腊人用来绘制几何图形的简陋工具与现代代数的自然运算完美匹配:加法 (+),减法 (−),乘法 (×),除法 (/) 和开平方根 (√)。原因在于直线和圆的方程仅使用这五种运算,这是欧几里得在代数前时代无法想象的观点。
您可能会惊讶地得知,高斯实际上从未绘制过正十七边形。他不需要这样做。他通过仅用圆规和直尺允许的五种代数运算来表示特殊长度 x[cosine (2π⁄17)],从而证明了该形状在原则上是可构造的。即使您不觉得他的方程特别有启发性,它的复杂性也表明了这位青少年必须为此问题投入了多少工作。

更令人印象深刻的是,高斯完全描述了哪些正多边形是可构造的,哪些不是(尽管直到1837年,皮埃尔·万策尔(Pierre Wantzel)才提供了严格的证明,表明高斯的描述没有遗漏任何内容)。因此,高斯不仅描述了所有可构造正多边形的形式,而且他和万策尔还证明了长期以来令人困惑的正七边形(七条边)和正十一边形(十一条边)不可能仅用圆规和直尺构造,正如无数其他形状一样,从而证实了欧几里得的挫败感。
根据传记作家G. Waldo Dunnington的说法,高斯对破解这个千年难题感到非常自豪,并告诉一位朋友他希望在他的墓碑上展示一个正十七边形。遗憾的是,他没有如愿以偿,但在高斯的出生地德国不伦瑞克市的一座纪念碑的背面刻着一颗17角星。石匠选择了一颗星星,因为他认为人们无法区分正十七边形和圆形。我想知道欧几里得是否会同意。