通常,数学中有明确的答案——特别是当任务不太复杂时。但是,当涉及到2000年开始流行的睡美人问题时,仍然没有普遍的共识。哲学和数学领域的专家分为两个阵营,并不停地引用——通常非常令人信服——各自立场的论据。关于这个谜题已经存在100多篇技术出版物,几乎每个听到睡美人思想实验的人都会形成自己强烈的观点。
困扰专家们的难题如下:睡美人同意参加一个实验。周日,她被给予安眠药并入睡。然后,实验者之一抛掷一枚硬币。如果“正面”朝上,科学家们会在周一唤醒睡美人。之后,他们会给她服用另一片安眠药。如果“反面”朝上,他们会在周一唤醒睡美人,让她重新入睡,并在周二再次唤醒她。然后他们再给她服用一片安眠药。在这两种情况下,他们都会在周三再次唤醒她,实验结束。
这里重要的是,由于安眠药的作用,睡美人不记得她之前是否被唤醒过。因此,当她醒来时,她无法区分是星期一还是星期二。实验人员也没有告诉睡美人硬币投掷的结果或当天是星期几。
然而,每次她醒来后,他们都会问她一个问题:硬币正面朝上的概率是多少?
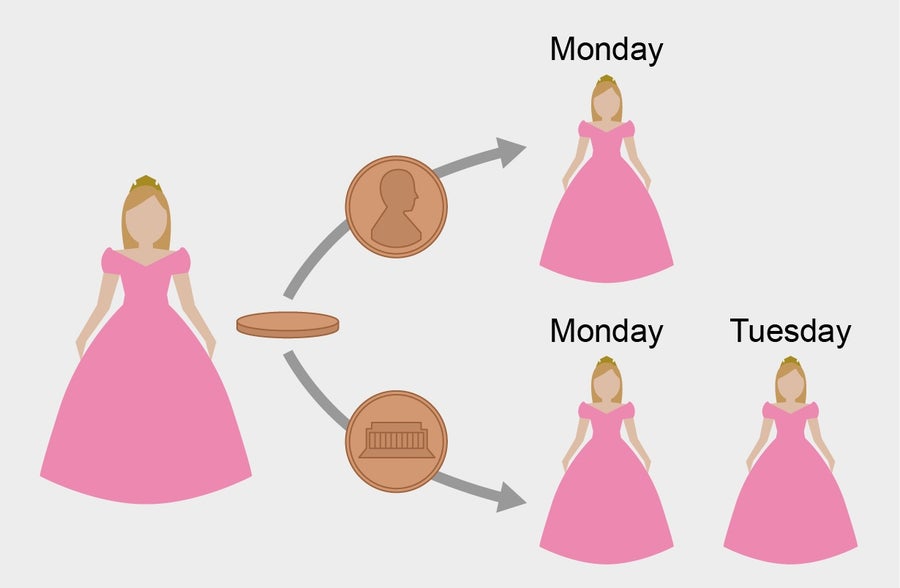
根据硬币投掷的结果,科学家们会唤醒睡美人一次(正面)或两次(反面)。 来源:Spektrum der Wissenschaft/马农·比肖夫,由《大众科学》设计
把自己放在睡美人的位置:你醒来,你不知道是星期几,你也不知道你之前是否被唤醒过。你只知道实验的理论过程。
我的第一直觉是睡美人应该猜½。无论实验的其余部分如何,硬币正面或反面朝上的概率始终为50%。美国哲学家大卫·刘易斯在得知这个问题时也持有相同的观点。毕竟,甚至可以在送睡美人睡觉之前抛掷硬币。根据实验的设计,她没有任何额外的线索来了解情况,因此逻辑上她应该将概率定为½。
但是,也有令人信服的论据支持概率为⅓。如果你仔细思考睡美人的经历,那么可能会发生三种情况
她在星期一醒来,抛掷的是正面。
她在星期一醒来,抛掷的是反面。
她在星期二醒来,抛掷的是反面。
每种事件的概率是多少?你可以从数学上和经验上对此进行研究。假设你抛掷硬币100次,得到反面52次,正面48次。换句话说,星期一/正面情景发生48次,而星期一/反面和星期二/反面情景各发生52次。
由于星期二/反面总是紧随星期一/反面之后,因此所有三个事件的概率都是相等的——因此必须是⅓。当睡美人被唤醒并被要求回答硬币投掷正面朝上的概率是多少时,根据这种推理,她应该回答⅓。

如果在100次抛掷后,你得到正面48次,反面52次,你可以将这些数字应用于睡美人的星期一和星期二情景。你会发现这三种情况或多或少同样可能发生。 来源:Spektrum der Wissenschaft/马农·比肖夫,由《大众科学》设计
普林斯顿大学的科学哲学家亚当·埃尔加,他在2000年普及了睡美人问题,得出了这个结论。他以数学上合理的方式阐述了他的论点。如果睡美人醒来时被告知今天是星期一(M),那么星期一/正面(M,H)和星期一/反面(M,Z)的概率无疑是相等的:P(M,H)= P(M,Z)= ½,其中P代表概率。另一方面,如果睡美人醒来并得知抛掷的是反面,那么那天可能是星期一或星期二(T),这意味着P(M,Z)= P(T,Z)= ½。
根据条件概率的计算,由此得出,在一般情况下(睡美人没有收到任何额外信息的情况下),这三个值是相等的:P(M,Z)= P(M,H)= P(T,Z)。由于所有三个概率必须加起来为1,因此每个单独的值为⅓。换句话说,由于在反面的情况下,睡美人被唤醒的次数是正面的两倍,因此从埃尔加的观点来看,她应该回答⅓。
走向极端
既然你已经听到了两个主要的论点,你现在会如何回答这个问题?为了更好地理解睡美人问题,思考更极端的思想实验版本可能会有所帮助。
假设在反面的情况下,睡美人不仅会在第二天额外被唤醒和提问一次,而且会被唤醒一百万次(大概以更小的时间间隔——因为即使对于童话人物来说,这个时间表也是残酷的)。如果你唤醒她并问她硬币正面朝上的概率是多少,那么答案½在这种情况下似乎不合逻辑。如果硬币投掷结果为反面,睡美人会被连续提问一百万次,而在正面的情况下,她只会被提问一次。
但是极端情况也可以加强½阵营的立场。例如,可以使用体育博彩代替抛硬币,例如退役短跑运动员尤塞恩·博尔特对阵歌手泰勒·斯威夫特的赛跑。在这种情况下,如果博尔特(多项跑步类别的世界纪录保持者)击败这位流行歌星——正如大多数人所预期的那样——睡美人只会在星期一醒来一次。但是,如果与所有预期相反,斯威夫特证明更快,睡美人必须每天醒来一个月,连续30次。博尔特输给斯威夫特的概率非常低。但是,如果我们应用与激励⅓回应相同的逻辑,我们需要同等看待这些情景。睡美人仍然需要在醒来后押注斯威夫特获胜,因为在这种——诚然不太可能的——情况下,她可能会被唤醒30次。刘易斯认为这个论点是荒谬的。因此,他认为这个思想实验支持½阵营。
你现在完全困惑了吗?你不是孤身一人。你的观点改变了吗?我的改变了。无论如何,我不再完全信服½阵营。我也能从⅓立场中获得启发。
这个谜题有一些有趣的应用。哲学家和数学家可以用它来广泛地思考决策和概率。例如,这个思想实验说明了一个人的信念——在这种情况下是睡美人的信念——如何导致不止一个理性的结论。它还强调了实验可能性的数量(例如抛掷正面与反面)与实验内部某人的可能经历之间的差异。
本文最初发表在《光谱》杂志上,并经许可转载。
