2018年,据报道,在纽约市,一只猫从32层公寓的窗户坠落到坚硬的沥青路面上——并幸存了下来。在兽医那里接受了两天的治疗,兽医治疗了它的肺塌陷和牙齿断裂后,这只四条腿的朋友得以重返家园。其他类似的事件很可能促成了猫有九条命的说法。几十年来,来自广泛学科的研究人员一直试图了解它们惊人的生存技能。
但让19世纪末的物理学家感到困惑的,并非动物从令人眩晕的高度坠落。相反,专家们被猫在坠落时绕自身轴旋转然后脚先着地的照片难住了。当时的图像显示,一个人抓住猫的腿,使其背部朝向地面。然后将动物放开。起初,猫科动物背部朝下,倒悬在空中。但在接下来的照片中,发生了一些似乎违反物理定律的事情:猫翻身并脚先着地。
当然,人们从日常观察中知道,这些四足动物可以在空中翻身。但人们一直认为,它们是通过从坠落的表面上蹬踏来获得这种运动所需的动量。这是因为根据角动量守恒定律,一个没有旋转的物体不可能在没有外部影响的情况下突然旋转。然而,这正是照片所显示的。最初,猫笔直下落。然后它设法绕自身轴旋转。这怎么可能呢?
支持科学新闻事业
如果您喜欢这篇文章,请考虑订阅以支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
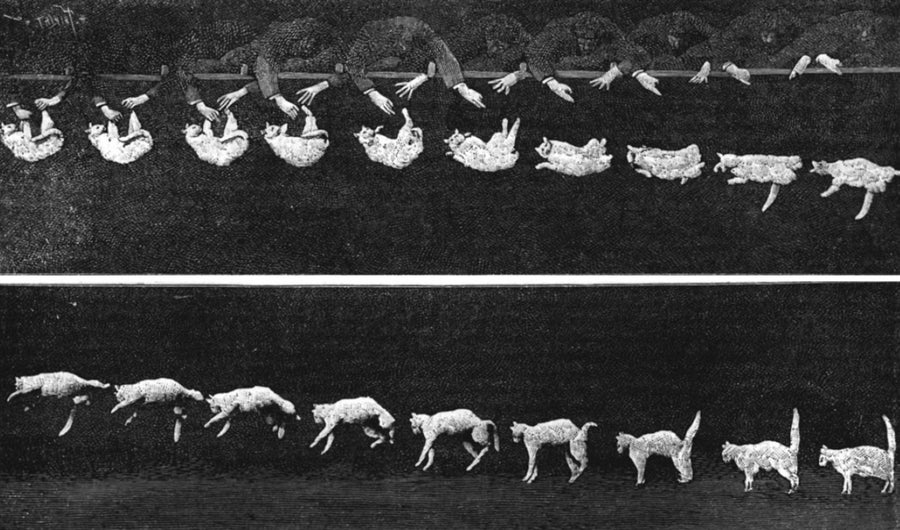
几十年来,坠落的猫一直困扰着物理学家。这些照片拍摄于 1894 年。图片来源:The Picture Art Collection/Alamy Stock Photo
这种现象引起了许多科学家的关注,包括以其电磁学研究而闻名的物理学家詹姆斯·克拉克·麦克斯韦。他进行了多次实验,将猫从不同的高度(包括从敞开的窗户)掉到床和桌子上。但直到 1969 年,“坠落猫问题”才得到解决。事实证明,人们对猫的身体没有进行足够仔细的考虑。它不仅仅是一个神奇地开始旋转的圆柱形物体。如果您仔细观察,您会发现猫的上半身和下半身朝相反的方向旋转。因此,角动量守恒定律得以保留。如果动物像胡椒研磨器一样朝两个不同的方向旋转,则角动量的变化为零。
但是猫是如何设法脚先着地的呢?为了做到这一点,猫科动物利用了经典力学的物理定律:通过将前爪靠近身体,它们减小了惯性矩。就像花样滑冰运动员一样,它们的上半身绕自身轴快速旋转。然后,动物用后腿采用相反的效果。它们伸展腿部,以产生尽可能大的惯性矩。结果,上半身旋转了很大的角度,而后腿朝相反的方向旋转的角度较小。动物极其灵活的脊柱使这种运动成为可能。一旦上半身处于正确的位置(即头部在地面上方垂直对齐),猫就可以伸出前爪,收紧后腿,并朝相反的方向执行类似胡椒研磨器的运动,从而使后爪也在地面上方对齐。通过这种方式,动物总是设法四肢着地——遵循所有物理定律。
猫能从多高的高度坠落并幸存下来?
物理定律表明,坠落高度越高,冲击力越大。但 1980 年代的一项研究描绘了不同的景象——至少对于猫而言是这样。两位纽约市兽医描述了 1984 年 6 月至 11 月期间共 132 例猫从高层建筑的 32 层楼坠落的案例。总体而言,90% 的猫幸存了下来。当兽医记录伤情时,他们做出了一个令人惊讶的观察:虽然损伤的严重程度在约七层楼的高度内有所增加,但之后似乎有所下降。换句话说,从 11 楼坠落对猫来说可能比从 6 楼坠落更温和。
猫科动物似乎再次打破了物理定律。身体坠落的楼层越高,受到地球引力加速的时间就越长。因此,它的速度应该越来越快,直到最终撞击地面。突然的撞击将动物从坠落中获得的动能转化为其他形式的能量,这可能导致骨折、肺塌陷以及更糟的情况。因此,从高层坠落应该比从低层坠落产生更令人不快的后果。
但是,这种思考猫科动物自由落体的方式忽略了空气阻力。毕竟,猫不是在真空中坠落到地面,而是在空气中移动,空气可以减缓它们的坠落速度。因此,在猫坠落过程中,有两个相反的力作用在它身上:重力Fg和阻力FR,阻力会减慢它的速度。虽然Fg的形式非常简单,仅仅是猫的质量m和重力加速度g的乘积,但空气阻力取决于横截面积A、阻力系数cW、空气密度ρ和坠落物体的速度v:FR = ½ x ρ x A x cW x v2。在坠落开始时,猫的速度为零,因此只有重力加速度作用于它,但是随着v的增加,相反的摩擦力就会显现出来。因此,要确定动物的具体运动,必须计算总力(Fg – FR)。然后,这决定了作用在一定重量m的猫身上的加速度:m x a = Fg – FR。
坠落猫的速度极限
加速度对应于速度的变化,可以用导数在数学上表示,a = d⁄dt v。因此,如果您想计算猫在某个时刻的速度,您必须求解一个复杂的方程组,该方程组既包含速度本身又包含其导数(加速度):m x d⁄dtv = m x g −½ x ρ x A x cW x v2。对于这种微分方程,通常没有精确解。在这种情况下,可以计算对应于双曲正切的速度解。根据猫的横截面和体重,您最终会得到一条曲线,该曲线在开始时快速增长,然后趋于平缓并收敛到恒定值:动物在坠落开始时速度很快增加,然后空气阻力最终变得非常强,以至于它不再加速,正如东南路易斯安那大学的物理学家莱特·阿兰为Wired计算的那样。
.png?w=900)
猫从更高的高度下降时,速度不一定会更快。图片来源:Spektrum der Wissenschaft/马农·比肖夫,Buckyball Design 设计
您还可以非常容易地计算出这个末速度或最大速度限制。因为当摩擦力与重力完全相等时,就会产生末速度,在这种情况下,这两个力相互抵消,坠落的物体以恒定速度坠向地面。因此,您只需要求解方程 m x g = ½ ρ A cW v2中的v,您就会得到:v = √(2mg⁄ρAc)。
要给出猫的末速度的具体值,只需要插入变量的数值即可。虽然可以估计猫的体重和横截面积,但阻力系数更难确定。假设一只猫重 4 公斤(约 8.8 磅),长 50 厘米(约 19 英寸),宽 15 厘米(近 6 英寸)。这些测量值将使动物的横截面积为A = 0.075 平方米。猫也可能具有圆柱体的阻力系数 (cW = 0.8)。那么动物的最终速度为:v = 32.68 米/秒,相当于略低于 120 公里/小时(或 74.5 英里/小时)。
为了找出猫在什么高度达到这个末速度,可以求解微分方程,从而计算出作为坠落高度函数的撞击时的速度。
.png?w=900)
可以根据猫的坠落高度计算出猫科动物的末速度。图片来源:Spektrum der Wissenschaft/马农·比肖夫,Buckyball Design 设计
从图中可以看出,猫在 100 米的坠落高度时已经达到了 30 米/秒的速度。由于已经观察到猫从更高的建筑物(例如从 32 楼)坠落后幸存下来,因此理论上它们可以在最大可能的 120 公里/小时的末速度下幸存下来。因此,从理论上讲,这些动物可以从任何可以想象的高度坠落中幸存下来。
实际效应还是幸存者偏差?
但是,这种末速度计算并不能解释纽约兽医的观察结果:为什么猫似乎从七楼或更高楼层坠落比从较低楼层坠落更能幸存下来?一种解释涉及动物的经验。
当猫从较低的高度坠落时,它会在短时间内处于失重状态。因此,本能地,它会伸出下面的腿以四肢着地。然而,在高坠落高度下,这种策略没有用:对齐的腿可能会导致严重的伤害,因为动物的重量分布不当。这种差异可能解释了为什么生存率会随着高度的增加而降低——至少在七层楼以内是这样。但是,在更高的坠落高度下,摩擦力在坠落过程中变得明显。这就是为什么,兽医推测,猫不再有坠落的感觉。因此,它可以放松,并且不会伸展腿。它着陆更柔和,重量分布更均匀,因此,生存机会更高。
但是,对于这种观察结果还有一种更简单的解释——尽管对于动物爱好者来说,这是一种更令人沮丧的解释。兽医的发现可能反映了所谓的幸存者偏差。如果一只猫从高层坠落并当场死亡,主人可能不会费心去兽医诊所。因此,未报告的死亡人数可能高于医疗专业人员记录的人数。
本文最初发表于《科学世界》,经许可转载。
