在高中统计学课上,我的老师提出了一个概率问题,至今仍困扰着我。这是一个谜题,灵感来源于电视游戏节目《让我们做个交易》,并以其长期主持人,已故的蒙提·霍尔的名字命名。设置很简单
您面前有三扇门。

其中一扇门后是一辆新车。另外两扇门后是山羊。
主持人邀请您选择一扇门,任意一扇门。

假设您选择了一号门。

主持人打开了您未选择的其中一扇门,露出一只山羊。

然后主持人给您选择,是否将您的选择改为二号门。
您应该坚持选择一号门,还是应该换成二号门?
大多数人认为坚持最初的选择还是换成另一扇未打开的门都无关紧要,因为概率是五五开——这只不过是掷硬币而已。但您应该总是换门。如果您换门,您有三分之二的几率获胜;如果您不换门,则只有三分之一的几率获胜。换句话说,换门会让您的获胜机会翻倍。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
这个违反直觉的问题,最早在1975年与电视节目联系起来描述,在世界各地的入门数学和统计学课程中都有教授。但它在1990年《Parade》杂志上被广泛普及。在作家玛丽莲·沃斯·萨文特在她的“问玛丽莲”专栏中写到这个谜题后,她收到了约10,000封愤怒的信件,宣称她给出的答案是错误的,其中包括约1,000封由拥有博士学位的人签署的信件。整个事件非常引人注目,以至于登上了《纽约时报》的头版。
概率怎么不是五五开呢?自从那个命运攸关的专栏以来,数学家、心理学家和哲学家一直在试图理解是什么让这个答案如此难以理解。他们发现,一些最常见的认知偏差可能是罪魁祸首,以及对概率如何运作的核心误解。“几乎每个人,即使是那些受过良好数学训练的人,对蒙提霍尔困境也会采取错误的直觉方法,”惠特曼学院的比较心理学家沃尔特·赫布兰森说。“而这表明他们拥有一个功能完全正常的人类大脑。”
在过去的十年里,我一次又一次地重新审视这个问题,我成了所有这些偏见和推理错误的受害者。最终,理解为什么概率不是五五开需要一个令人费解的视角转变。
最直接地理解为什么您应该总是换门的方法之一是画出所有可能的结果。假设您选择了一号门。有三种可能的现实:汽车在一号门、二号门或三号门后。
如果汽车在二号门后,蒙提·霍尔将打开三号门,并让您选择换成二号门。换门会得到正确的门。
如果汽车在三号门后,蒙提将打开二号门,并让您选择换成三号门。换门会得到正确的门。
如果汽车确实在一号门后,蒙提将打开二号门或三号门中的任意一扇,并让您选择换成他没有打开的那扇门。换门会得到错误的门。
简而言之,如果您最初选择了正确的门(这种情况发生的概率是1/3),当您被提供机会时,您不应该换门。如果您最初选择了错误的门(这种情况发生的概率是2/3),您应该换门。
这个基本的决策树证明了两件事:概率不是五五开,而且如果您总是换门,您会更好。然而,心理学研究表明,人们不仅通常认为选择是五五开,而且他们还决定坚持最初的门,大约占85%到90%的时间。更重要的是,社会心理学家、维克森林大学的约翰·彼得罗切利说,即使有越来越多的证据表明他们不应该这样做,他们通常还是会继续选择坚持不动。彼得罗切利让参与者一遍又一遍地玩蒙提霍尔游戏,让他们反复观察到奖品更常在“换门”后面——但这些参与者花了多次试验才学会他们应该换门。
然后他用一系列简单的抛硬币进行了测试。想象一下,您反复抛硬币,每次都押注结果。您需要多久才能注意到硬币是有偏差的,正面朝上的概率是2/3而不是1/2?
“大多数人认为他们会在大约40次抛掷后开始意识到这一点。但他们并没有,”彼得罗切利说。他的研究将这种学习不足归因于他称之为“当头棒喝”思维,或反事实思维。在我们做出决定后,我们经常通过告诉自己“如果我选择了不同的选择,我可能会赢”来模拟我们没有做出的选择的结果。如果您坚持最初的门并输了,这种反事实可能并不那么突出,但当您换门并输了时,它们会非常突出——可能是因为拥有过又失去比从未拥有过感觉更糟糕。彼得罗切利说,这些与现实竞争的替代方案会模糊您的记忆,“您将看不到正在您面前出现的模式。”
即使当他们了解问题的工作原理时,许多人也不相信他们应该换门。那是因为上面的解释,虽然优雅而准确,但并不令人信服——不仅仅是对像我这样的统计学学生来说。即使是多产的数学家保罗·埃尔德什也栽了跟头,据他儿时的朋友和同事数学家安德鲁·瓦佐尼说。在1999年《决策科学研究所》出版物《决策专线》的一篇文章中,瓦佐尼描述了埃尔德什第一次被他的朋友提出这个问题时变得慌乱,要求解释他为什么要换门,然后在瓦佐尼没有提供解释时回应“你怎么了?”。“我说我很抱歉,但我没有一个常识性的解释,”瓦佐尼回忆道。
如果您告诉统计学教授您对蒙提霍尔问题感到困惑,他们通常会提供一个常识性的解释。想象一下有100扇门而不是三扇。只有一扇门后有一辆汽车,其他99扇门后都是山羊。您选择一扇门,比如,一号门,然后蒙提沿着队伍走,一扇接一扇地打开门。他直接跳过了72号门,让它保持关闭,然后打开了剩下的门。您是想坚持选择一号门还是换成72号门?在这里,如果您换门,您真的应该换门。如果您这样做,您的获胜机会是99%。
“人们通常会在那时相信您,”詹姆斯麦迪逊大学的数学家杰森·罗森豪斯说,他写了一本关于蒙提霍尔问题的书。“但这并没有完全触及问题核心的数学问题。”
他是对的:在听完100扇门的解释后,我相信正确的选择是换门——但只是勉强相信。五五开的概率的想法有一种引力,我感觉我无法逃脱。我一直被一个令人困惑的问题困住:为什么我对三扇门中的第一选择似乎会“影响”我在换门和坚持之间的第二选择?我的直觉是,概率应该在两个选择之间重置,第二个选择与第一个选择无关。
“这种[假设]非常自然,而且似乎非常明显,但实际上是错误的,”罗森豪斯说。那是因为蒙提·霍尔知道汽车在哪扇门后,并且他会相应地选择他的“戏弄揭示”门。如果他没有这样做,而是随机打开两扇未选择的门中的一扇——让他真正有机会意外地揭示汽车——那么您的“坚持还是换门”的选择确实是五五开。但蒙提的知识和约束改变了一切。要完全理解为什么这是真的,您需要站在蒙提的角度思考。
去年,当我向我的朋友和她的父亲——他教军事战略和博弈论——解释我对这个问题的爱恨交加的关系时,我们决定设置游戏,以便我们可以亲自玩它。我把一颗花生M&M放在三个杯子中的一个下面,并扮演了蒙提·霍尔的角色。在断断续续地沮丧了10年后,一切终于豁然开朗。
尝试站在蒙提的角度思考
让我们再玩一次。这次,您是主持人。
您知道每扇门后是什么,但玩家不知道。
您要求玩家选择一扇门。
偶尔——平均每三次中一次——玩家会随机选择一扇藏有汽车的门作为他们的首选。在这一轮中,那是三号门。
作为主持人,您然后可以打开另外两扇门中的任意一扇,因为它们都藏着山羊。(主持人只能选择揭示山羊。)
您打开二号门,露出一只山羊。
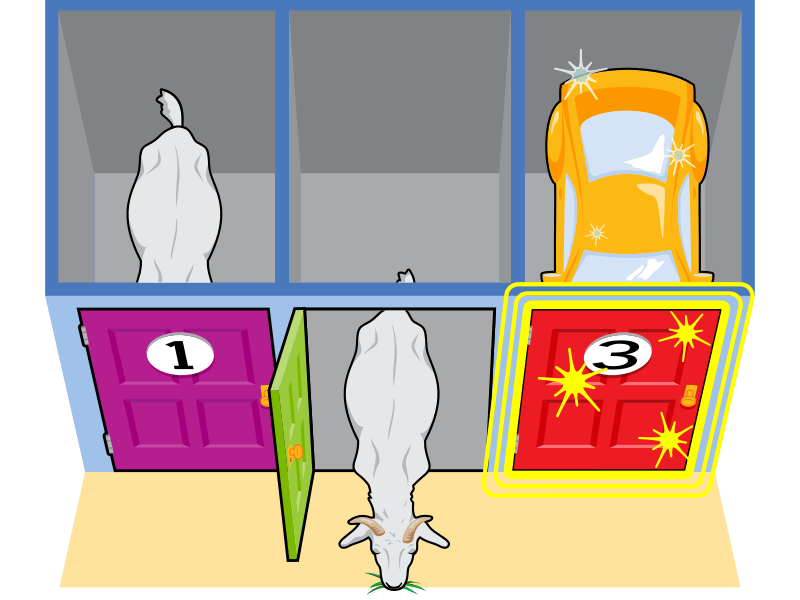
然后您给玩家选择,是否将他们的选择改为一号门。

在这种情况下,如果玩家坚持他们最初的选择,三号门,他们就会获胜。
但更常见的情况是——每三次中有两次——玩家会选择一扇藏着山羊的门作为他们的首选。
让我们重置游戏。在这一轮中,玩家首先选择一号门。

作为主持人,您现在必须打开另外两扇门中的一扇。您不能选择汽车。
因此,作为主持人,您唯一的选择是三号门。您打开三号门,露出一只山羊。
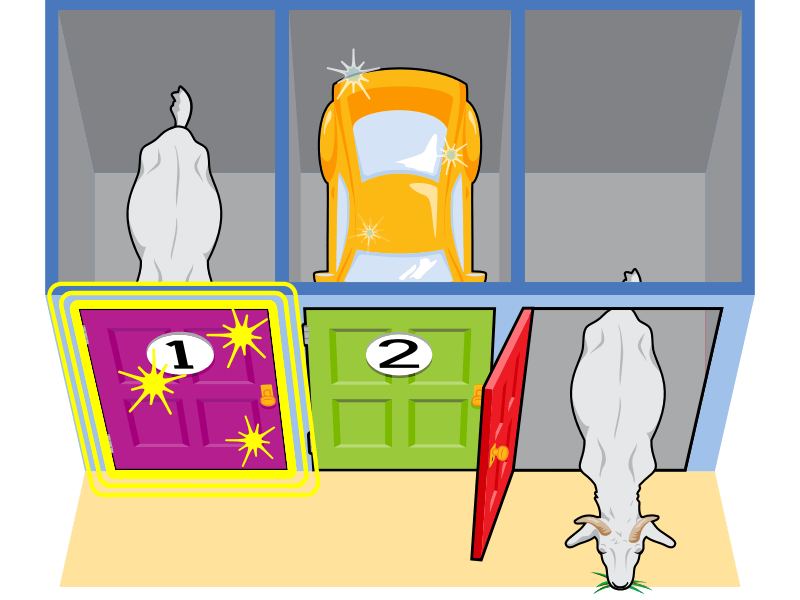
现在您给玩家选择,是坚持选择一号门还是换成二号门。
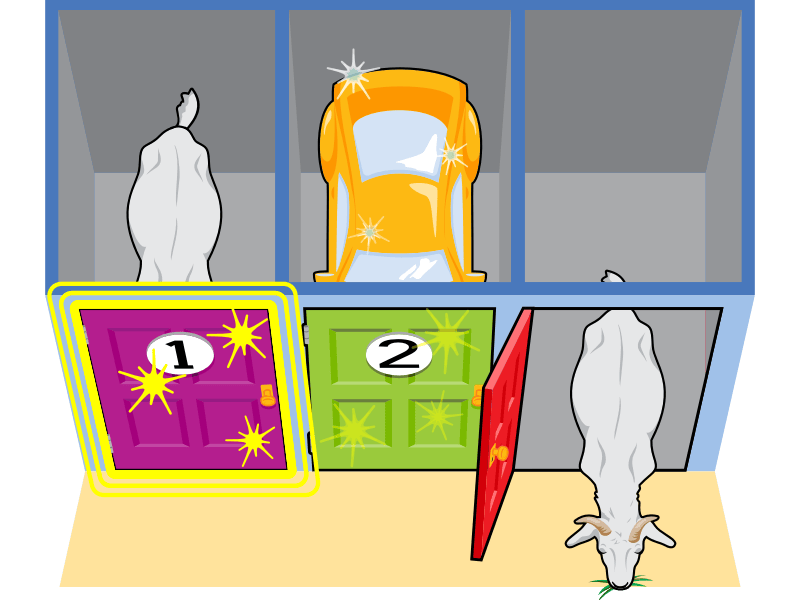
如果他们坚持,他们就会输。如果他们换门,他们就会赢。
所以,是的,即使在三分之一的情况下,玩家可能会首先选择汽车,并从不改变主意中获益……

……但从统计学上讲,玩家始终更换他们的门选择才是最符合他们利益的。
从扮演参赛者转变为扮演主持人有助于许多人理解为什么他们应该换门。在2003年的一项研究中,研究人员发现,从蒙提的角度玩游戏的人比那些作为参赛者玩游戏的人更倾向于说游戏节目参与者应该换门。(他们还必须被提示思考如果参与者选择了三扇门中的每一扇会发生什么。)彼得罗切利和他的同事在他们自己的研究中也有同样的经历。他说,将问题编程到他们的研究中,使换门具有如此优势的原因“非常清楚”。
当您扮演主持人时,您可以看到的是:蒙提·霍尔不是什么神秘人物,做出一些阴暗的决定来操纵、欺骗或以其他方式欺骗参赛者。事实上,蒙提几乎没有做出任何有意义的决定——以至于扮演主持人几乎很无聊。在三分之二的游戏中,参赛者第一次选择了一只山羊,这意味着主持人在他们打开哪扇门来戏弄他们时没有选择。在三分之一的游戏中,参赛者第一次选择了汽车,因此主持人随机在两扇山羊门之间选择进行戏弄揭示。
虽然戏弄揭示对参赛者来说感觉像是新的和重要的信息,但蒙提看到这只是一种干扰。主持人告诉参赛者一些他们已经知道的事情:“嘿,这两扇门中的一扇肯定没有汽车。”作为蒙提,您看到通过打开一扇山羊门,您不是在给他们信息——您是在给他们一个机会。
这个机会是以一扇门的价格获得两扇门的概率。在这样的游戏中,您不能选择两扇门。但这实际上是参赛者在决定换门时所做的事情。
像这样想象一下:您是参赛者,您选择三号门。然后主持人问您是否想换成一号门和二号门。当然,是的——如果这是一个选项,您当然会选择两扇门。然后主持人打开一号门,露出一只山羊。您仍然想坚持选择一号门和二号门,还是换成三号门?您坚持选择一号门和二号门,因为没有任何改变。您已经知道您的两扇门中的一扇包含一只山羊。那是旧闻了。但您仍然有2/3的几率您的选择包含获胜的门。您的两扇门中的一扇被打开,而您所有的希望现在都寄托在另一扇门上的事实是完全无关紧要的。
当戏弄揭示门被打开时,“人们认为一切都改变了,但情况与最初相同,”巴塞罗那大学的心理学家伊丽莎白·图鲍说。那“是问题中的错觉”。
“这几乎就像一个魔术,对吧?”研究逻辑和科学哲学的西方伊利诺伊大学的哲学家克里斯托弗·潘尼斯说。您可能看到面前有两扇可能的门,但这只是一些巧妙的障眼法。您真正押注的不是一扇门与另一扇门,而是您第一次选择正确的概率与您没有选择正确的概率。您有机会押注您的最初选择,由于抛弃式的戏弄揭示,两扇门的概率被折叠成一扇门。
蒙提霍尔困境在这里利用了一种叫做等概率偏差的东西:我们假设所有呈现的结果都同样可能。比利时鲁汶大学研究科学方法论和统计学的帕特里克·翁格纳解释说,在一种夸张的形式中,这就像掷骰子,并询问某人您掷出一点或“非一点”的几率是多少。如果您不了解骰子是如何工作的,您可能会错误地认为赔率是五五开,因为呈现给您的是两个选项。但是,一旦您了解骰子有六个面,您就会明白这两个选择并不等同。
虽然我现在已经获得了蒙提霍尔顿悟,但以“正确”的方式思考这个问题仍然感觉像是在扭曲我的思维。我仍然固执地回到那个问题:为什么一旦只剩下两扇门,概率就不能重置呢?
当我向潘尼斯询问这个问题时,他的回答揭示了我一生都对概率存在误解。“想象一下,您[在游戏进行到一半时]打开电视,只有两扇门。您什么都不知道,您选择了一扇门,”他说。“那是一个真正的五五开的选择。您没有第三个选择的选项,因为您是在之后才进入这种情况的。”
但与您不同,游戏节目参赛者如果换门,仍然有2/3的概率做对。那是因为我们一直在谈论的概率与门、汽车和山羊无关,而是与观察者有关。换句话说,概率在观察者的眼中。
这种更主观的概率思考方式是所谓贝叶斯推理的核心。托马斯·贝叶斯牧师是一位生活在18世纪的神学家,他从基于证据的确定程度的角度思考概率。他的定理可以利用事件发生的先验概率知识,并在新信息出现时对其进行更新。这种统计方法以个人做出估计为中心——以及这个人对不同结果可能性的了解。
今天,贝叶斯定理被用于测试疫苗、绘制宇宙地图和训练机器学习算法。但它不是科学家和数学家处理概率问题的默认方式。这个荣誉归于一种叫做频率主义推理的东西,它将概率更像是一种物理属性,可以通过重复测试或模拟来揭示。这枚硬币有偏差吗?频率主义者多次抛掷它以找出答案。我应该换门还是坚持不动?频率主义者运行许多计算机模拟,并看到汽车在2/3的时间里都在“换门”后面。在这里,这些事件的概率被视为一种物理事物,一种有待发现的客观真理。
不幸的是,这种方法对揭示蒙提霍尔困境的细微差别几乎没有作用。频率主义者,看着游戏节目的舞台,可能会将概率附加到门和汽车上,而不是附加到做出猜测的参与者身上。“我的假设,”瓦佐尼在保罗·霍夫曼的《爱数字的人》中说,“是埃尔德什认为概率是附加在物理事物上的,这就是为什么他不明白为什么换门是有道理的。”
当我问1990年《Parade》专栏的作者沃斯·萨文特,她认为蒙提霍尔困境的持久教训是什么时,她的回答不涉及统计学中的竞争理论。她说,这个谜题是关于谦逊。“它促进了对人类弱点的一种绝妙展示,”沃斯·萨文特解释说,“不相信我们可能会犯错,以及我们坚持早期判断的顽固,有时甚至是委屈,特别是当我们感觉确定的时候。”