打开您最喜欢的社交媒体平台,记下您有多少朋友或关注者。具体来说,记下这个数字的第一位数字。例如,如果您有400个朋友,则首位数字是4,如果您有79个朋友,则是7。假设我们要求很多人这样做。我们可能会预期各种各样的回应——普遍的直觉表明,朋友的数量应该在某种程度上是随机的,因此它们的首位数字也应该是随机的,1到9均匀分布。奇怪的是,这不是我们会发现的情况。相反,我们会看到一个明显的失衡,几乎一半的朋友数量以1或2开头,而只有可怜的10%以8或9开头。请记住,这与拥有更多或更少的朋友无关;1,000个朋友远远多于8个。
1和2这种奇怪的过度代表现象不仅限于朋友和关注者,还扩展到点赞和转发,甚至远远超出社交媒体,扩展到无数个数字世界的角落:国家人口、河流长度、山脉高度、死亡率、股票价格,甚至是典型《大众科学》杂志中发现的各种数字集合。不仅较小的首位数字更常见,而且它们还遵循精确且一致的模式。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
如果所有数字都均等地表示,那么它们中的每一个都将出现九分之一(约11.1%)的时间。然而,在惊人数量的真实世界数据集中,令人震惊的是,30.1%的条目以1开头,17.6%以2开头,依此类推。这种现象被称为本福特定律。即使您更改数据的单位,该定律仍然成立。以英尺或弗隆测量河流,以美元或第纳尔测量股票价格——无论您如何测量,这些首位数字的确切比例都保持不变。尽管数学家已经提出了几个聪明的理由来解释为什么这种模式可能会出现,但其纯粹的普遍性仍然无法用简单的解释来概括。
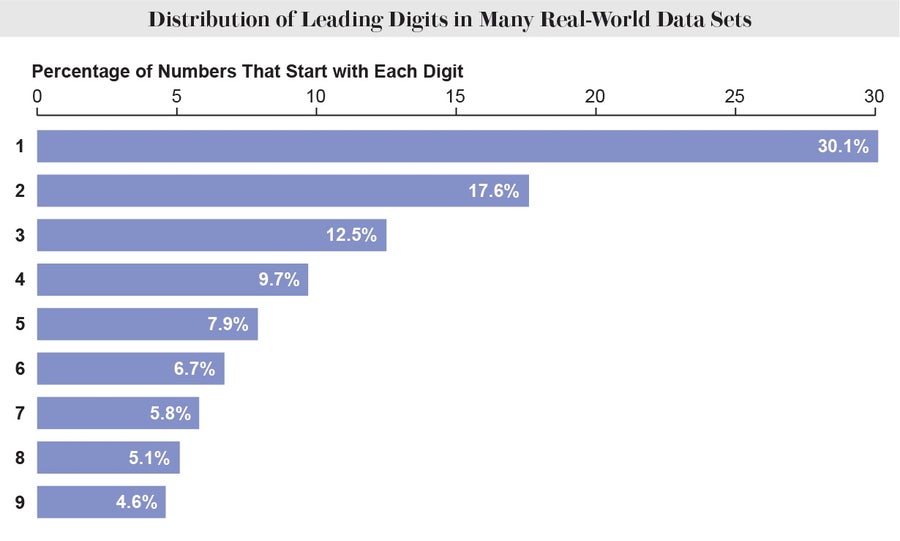
来源:Amanda Montañez;来源:Simon Newcomb在《美国数学杂志》第4卷第1期,1881年发表的“关于自然数中不同数字使用频率的注释” (数据)
碰巧的是,本福特并非第一个发现本福特定律的人。在计算器出现之前,人们将繁琐的算术外包给称为对数表的参考书。1881年,天文学家西蒙·纽科姆注意到,对数表的早期页面(对应于以1开头的数字)与后面的页面相比,显得肮脏和磨损。他推断,较小的首位数字在自然数据集必然更常见,并且他公布了正确的百分比。物理学家弗兰克·本福特在1938年也做出了同样的观察并普及了该定律,汇编了超过20,000个数据点来证明其普遍性。
该定律已被用于将人们送入监狱。当检察官在法庭上辩称金融顾问韦斯利·罗兹被判犯有欺诈投资者罪时,他的文件与预期的首位数字分布不符,因此可能是伪造的。该原则后来帮助计算机科学家詹妮弗·戈尔贝克揭露了Twitter上的一个俄罗斯机器人网络。她观察到,对于大多数用户来说,其关注者的关注者数量都符合本福特定律,但虚假账户则明显偏离该模式。本福特定律应用于欺诈检测的例子比比皆是,从希腊操纵宏观经济数据以申请加入欧元区,到I朗2009年总统选举中的舞弊行为。信息很明确:有机过程产生的数字倾向于较小的首位数字,而伪造数据的幼稚方法则不然。
为什么自然界会产生大量的1而缺少9?首先,重要的是要说明许多数据集不符合本福特定律。当以英尺为单位测量时,成年人的身高大多以4、5和6开头。轮盘赌落在以2开头的数字上的可能性与落在以1开头的数字上的可能性相同。该定律更可能适用于跨越多个数量级且从某些类型的随机过程演变而来的数据集。
指数增长是一个特别直观的例子。想象一下,一个岛屿最初居住着100只动物,其数量每年翻一番:一年后有200只动物,两年后有400只。我们已经注意到首位数字的一些奇怪之处。在整个第一年中,岛屿人口的首位数字都是1。在第二年,人口数量在相同的时间长度内跨越了200和300,从而减少了每个首位数字统治的时间。这种情况在第三年继续,从400到800,此时首位数字的更替速度更快。
原因是,例如,从1,000增长到2,000需要翻一番,而从8,000增长到9,000仅增长12.5%,并且这种趋势在每个新的数量级都会重置。我们岛屿示例中选择的参数没有什么特别之处。例如,我们可以从43只动物的人口开始,每年增长1.3倍,我们将看到完全相同的首位数字模式。几乎所有这种类型的指数增长都将趋向于本福特定律。
该定律对测量单位的顽固漠视提供了另一个关于为什么这种模式在自然界如此常见的暗示。无论我们以米还是英里记录河流长度,河流长度都遵循本福特定律,而非本福特定律兼容的数据(例如成年人的身高)在转换为米时会彻底改变其首位数字的分布,因为没有人是四米高的。值得注意的是,本福特定律是唯一对这种单位变化免疫的首位数字分布。
我们可以将更改单位视为将数据集中的每个值乘以某个数字。例如,我们将长度集合乘以1,609.34,以将其从英里转换为米。本福特定律实际上对更一般的变换具有弹性。取符合本福特定律的数据并将每个值乘以不同的数字(而不是固定的数字,例如1,609.34)将不会扰乱首位数字的分布。这意味着,如果自然现象是由几个独立来源的乘积产生的,那么这些来源中只需要一个符合本福特定律,整体结果就会符合。本福特定律具有蚕食性,就像一堆相乘的数字中的一个零使结果为零一样。
这些解释并不能解释为什么从《大众科学》杂志中挑选出来的各种数字集合会遵守本福特定律。这些数字不会呈指数增长,我们也没有将它们相乘。数学家特德·希尔发现了许多人认为是首位数字定律的最终证明。他认为,如果您从大量随机数据集中挑选大量随机数字,它们将趋向于本福特定律。换句话说,尽管无数数据集显示本福特模式,但体现它的最可靠方法是从不同的来源提取数字,例如我们在报纸上看到的那些数字。
我已经花了很多时间思考本福特定律,它仍然让我惊讶于它出现的频率如此之高。关注您在日常生活中遇到的数字,您可能会开始发现它的例子。
