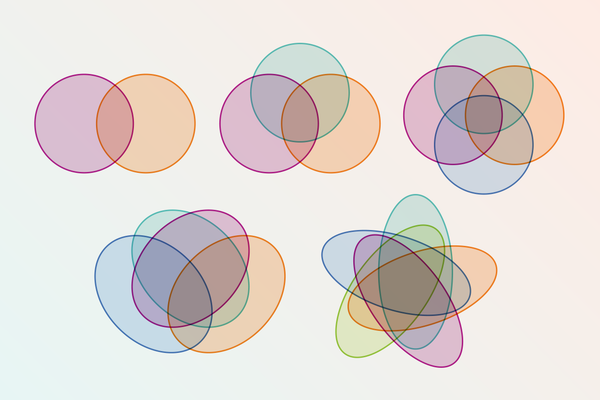在《数学宇宙》一书中,数学家威廉·邓纳姆这样评价约翰·维恩以其名字命名的遗产——维恩图:“在漫长的数学史上,没有人因为更少的东西而更出名。” 虽然维恩图可能没有解决任何长期存在的未解难题,但这些相互交错的圆环当然值得更多赞誉。它们对群体关系的简洁表示解释了它们在教室、信息图表和互联网迷因中持久的吸引力。
维恩图不仅仅是视觉辅助工具,它们还可以帮助我们解决日常逻辑问题,并引发令人惊讶的几何问题。您见过用四个重叠圆圈组成的合适的维恩图吗?没有,因为这是不可能的。维恩本人发现了这一点,并提出了一个巧妙的解决方案,但这仅仅引发了更深层次的几何难题,数学家们至今仍在研究。
维恩在1880年首次展示了他的图表,作为一种可视化逻辑学当代进展的方法。然后,它们在密切相关的数学分支——集合论中找到了应用,集合论专注于对象的集合。维恩图通常由重叠的圆圈组成,每个圆圈代表一组元素(例如,可爱的东西或百老汇演出)。两个圆圈之间的重叠区域包含属于两个集合的元素(例如,“猫”)。就像使用统计学中的散点图或几何学中绘制形状一样,看到问题通常可以澄清问题。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
想象一下,您正在计划一个晚宴,并在朋友们善变的偏好中周旋。如果威尔玛参加,那么弗雷德也会参加。如果巴尼参加,那么其他人也会参加。如果威尔玛来,巴尼就不会来,但如果她不来,他就会来。如果弗雷德和巴尼都参加,那么威尔玛也会参加。您应该期望谁会来?当我们只给出文本时,这个难题很难解决。维恩图提供了一种系统的方法来可视化和解决它。每个陈述都排除了某些可能的结果,我们通过对维恩图的相应区域进行阴影处理来表示这些结果。
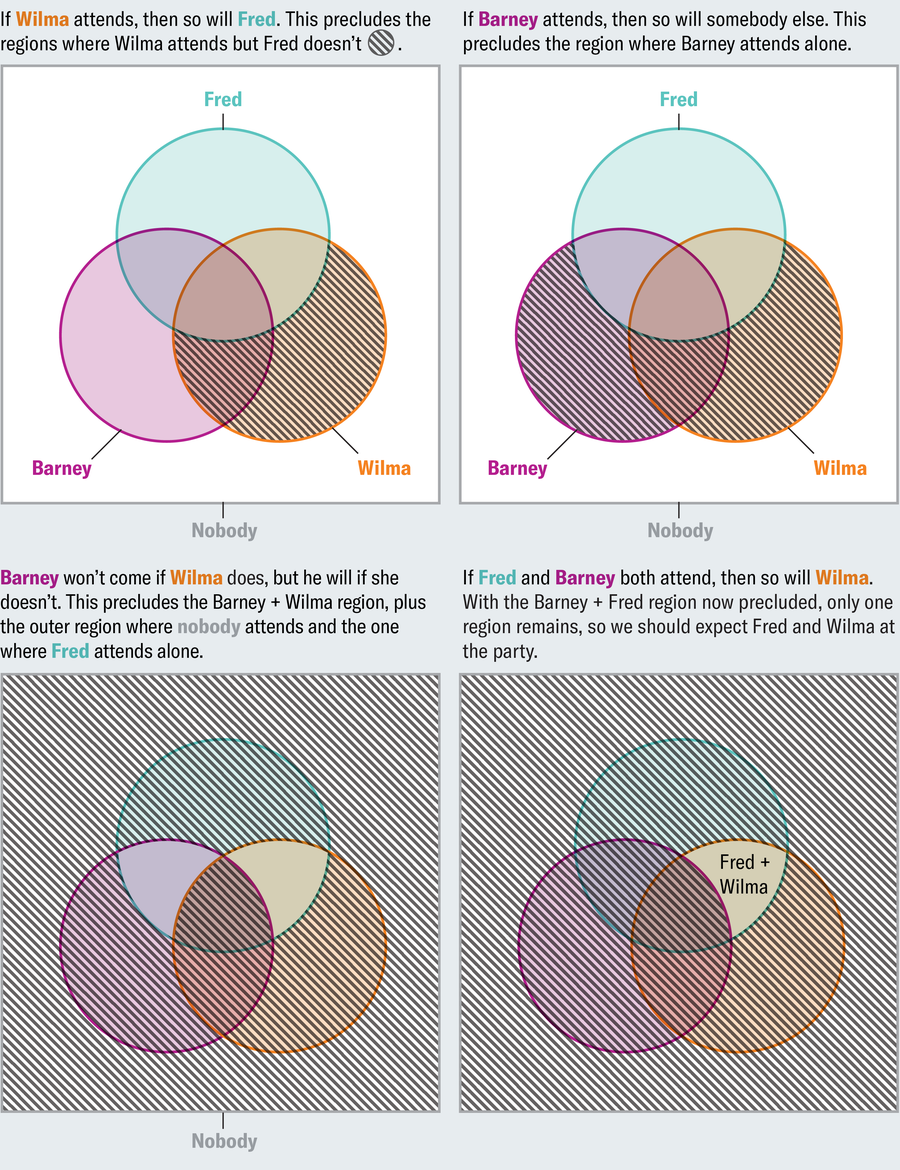
阿曼达·蒙塔涅斯
您遇到的大多数维恩图都描绘了两个或三个重叠的圆圈,但是如果您有四个或更多集合要考虑怎么办?
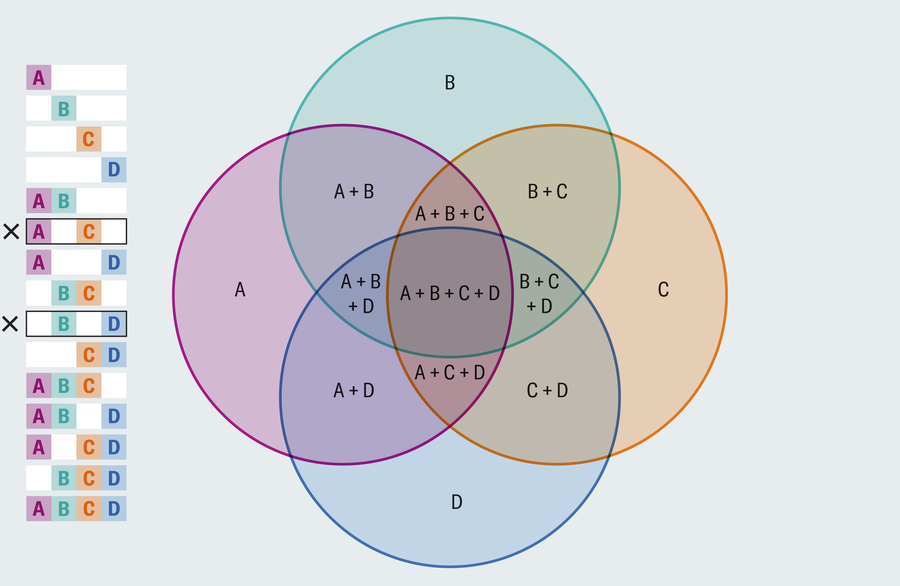
阿曼达·蒙塔涅斯
您发现问题了吗?没有一个区域仅包含A和C的重叠,而不包含另一个区域,B和D也是如此。一个合适的维恩图描绘了所有交叉点的组合。重新调整布局无济于事。每个四圆图都存在同样的缺陷。
要了解原因,请从一个圆圈开始,并注意它建立了两个区域——内部和外部。当我们添加第二个元素集合(一个新的圆圈)时,我们将可能性增加了一倍,因此我们需要将区域数量增加一倍(第一个集合、第二个集合、两个集合和两个都不是集合)。唯一的方法是让第二个圆圈在两点与第一个圆圈相交(仅在一个点接触将导致只有三个区域:第一个集合、第二个集合或两者都不是)。这种趋势持续下去,如果我们想表示所有逻辑可能性,则每个新圆圈都必须使区域数量翻倍。但是新区域的数量不能超过新的交点的数量,并且一个新圆圈只能在两个点与现有圆圈相交。当添加第三个圆圈时,这很好,因为我们需要添加四个区域,并且新圆圈可以在两个点与两个现有圆圈相交,总共四个新的交点。但是,当使用第四个圆圈时,它会崩溃,我们需要八个新区域,但只能聚集六个新的交点。
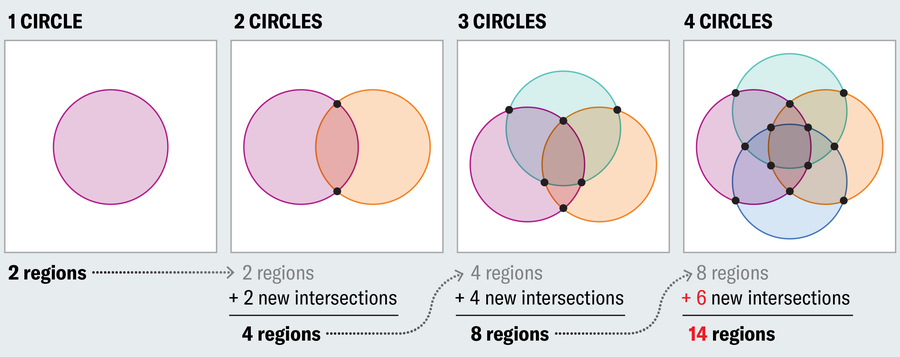
阿曼达·蒙塔涅斯
当然,我们不需要将自己限制在圆圈上。我们可以轻松地通过三圆图追踪一个弯曲的环,以便它划分出必要数量的区域,但我们会失去图表的优雅性。四个相交的球体也可以表示正确数量的区域,但是三维视觉效果很难解析。约翰·维恩知道圆圈的缺点,因此他提出了用椭圆来表示四个集合。
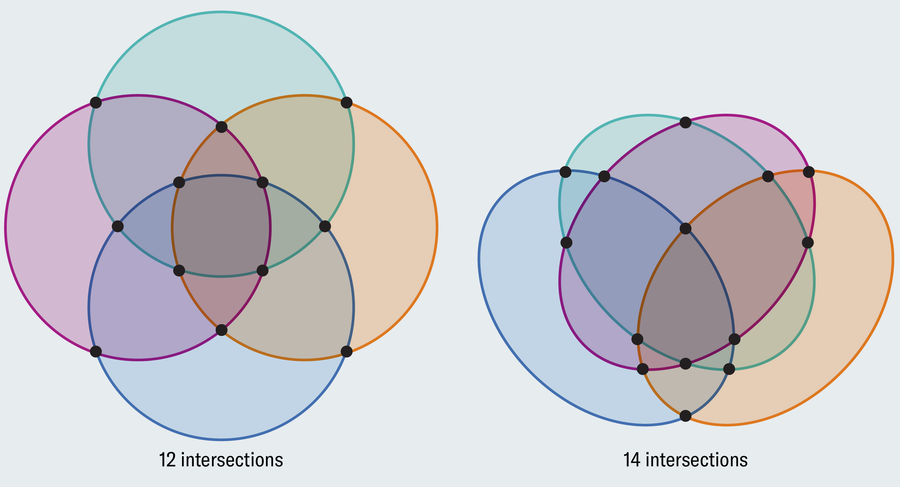
阿曼达·蒙塔涅斯;资料来源:“维恩图和集合的独立族”,布兰科·格林鲍姆著,载于《数学杂志》,第48卷,第1期;1975年1月 (参考文献)
与圆圈不同,两个椭圆可以在四个点相交。这克服了圆圈的局限性,但这只是暂时的。椭圆适用于四个和五个集合,然后以与圆圈相同的方式失效。随着集合数量的增长,我们需要越来越奇特的形状来描绘它们。
有人可能会合理地争辩说,超过四个元素集合,维恩图就失去了它们的效用。四椭圆图像已经非常混乱。也许对于五个或更多集合,我们应该放弃视觉表示。但是,效用并没有像美和好奇心那样激发数学家的兴趣。尽管维恩图最初应用于逻辑和集合论,但四圆难题提出了一个有趣的几何学问题。这个种子已经发展成为对维恩图几何学的迷人研究,并且一直延续至今。
维恩和他的继任者认为,椭圆无法描绘五个集合图所需的所有32个区域。直到1975年,数学家布兰科·格林鲍姆才通过实例证明他们错了

阿曼达·蒙塔涅斯;资料来源:“维恩图和集合的独立族”,布兰科·格林鲍姆著,载于《数学杂志》,第48卷,第1期;1975年1月 (参考文献)
另请注意,格林鲍姆的图表显示出令人愉悦的旋转对称性。将其旋转整整五分之一圈,它又会回到自身,使原始形状保持不变。典型的两圆和三圆维恩图也具有此属性。将两圆维恩图旋转180度(或将三圆维恩图旋转120度),它看起来还是一样。但是四椭圆图没有旋转对称性。这可以修复吗?二、三和五有什么共同之处,而四没有?
1960年,当时斯沃斯莫尔学院的本科生大卫·W·亨德森,通过一项惊人的发现回答了这个问题(斯坦·瓦根和彼得·韦伯后来填补了一些空白):只有当集合的数量是素数时,才有可能实现旋转对称的维恩图——素数是只能被1和自身整除的数字,例如2、3和5,但不是4。亨德森只表明素数个集合是必要的,而不是说您总是可以为每个素数设计对称的维恩图。因此,寻找越来越大的示例的竞赛开始了。这是一个看起来很狂野的来自彼得·汉堡的11个集合的维恩图。
南卡罗来纳大学的数学家在2004年解决了这个问题,他们证明了对于每个素数个集合都存在旋转对称的维恩图。如果您认为这导致数学家收拾铅笔,停止对维恩图的研究,那么您就没有继续关注。相反,社区提高了他们的审美标准,寻求具有更精致属性的图形。
我们开篇引用的内容认为维恩图被高估了。即使是那些同意这种观点的人也必须承认它们具有一种奇特的魅力。以逻辑学、几何学和可视化中感兴趣的主题集合为例,您会在交集处找到维恩图。