明日量子计算机威胁今日机密。以下是如何保护它们

全球数字安全专家都密切关注着 Y2Q——“量子时代还有几年”——时钟。它倒计时着预计的日期，届时量子计算机将能够破解现代密码学的一种重要形式。它被称为公钥密码学，因为它具有在公共场合共享密钥的巧妙方法，当您在网上购物时，它可以保护您的信用卡号安全，并确保您手机的软件更新来自电话公司而不是黑客。举报人使用它来联系记者，企业使用它来发送机密文件。

但是量子计算机将使标准的公钥密码学类型变得无用。“这真的非常严重，”云安全联盟量子安全安全工作组联合主席布鲁诺·胡特纳说。“如果明天出现量子计算机，我们将无法在任何安全保障的情况下进行对话。”

胡特纳是 Y2Q 时钟的创建者之一，其命名类比于 20 世纪 90 年代末的 Y2K 危机。20 世纪的软件程序用两位数字表示年份，这意味着对于计算机来说，2000 年是“00”——与 1900 年相同。涉及此类日期的程序预计在新千年到来时会发生故障，从而可能造成大规模中断。但最终，当年份改变时，没有银行倒闭，没有电网关闭，也没有飞机从天空坠落。过渡是无缝的——主要是因为企业和政府竞相修复了 Y2K 漏洞。

支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅，您将帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。

没有人确切知道何时会开发出足够大的量子计算机来破解密码学标准。Y2Q 时钟当前的截止日期 2030 年 4 月 14 日只是一个猜测。但大多数研究人员认为，这种转变将在未来几十年内发生。“威胁即将来临，”胡特纳说，Y2Q 时钟就是一个提醒。“确定一个日期有助于人们集中注意力。”

对于需要长期保密的政府和其他机构来说，真正的截止日期要早得多。如果今天发送的加密数据被存储起来，那么未来的量子计算机可能会追溯解密这些消息。“如果您需要保守秘密 20 年，并且您认为在 20 年内可能会出现破解您的密码学的量子计算机，那么您今天就遇到了问题，”密歇根大学的计算机科学家克里斯·佩克特说。

为了应对这一威胁，美国国家标准与技术研究院 (NIST) 于 2016 年发起了一项公开竞赛。它征集了“后量子”或“抗量子”密码学的想法——可以在今天的计算机上运行，但非常强大，即使是量子计算机也无法破解的代码。为了强调紧迫性，美国国会在 2022 年 12 月通过了《量子计算机网络安全准备法案》，该法案要求政府机构制定过渡到此类算法的计划。

经过四轮提交和评估后，NIST 在公钥加密类别中选出了一个获胜者，名为 CRYSTALS-Kyber，在用于安全识别消息发送者的数字签名类别中选出了三个获胜者。NIST 现在正在与研究人员合作，将获胜的算法标准化，以便程序员可以开始奠定防量子保密的基础。

然而，令人有些担忧的是，四个选定的算法中有三个，包括 CRYSTALS-Kyber，都是基于格数学。专家们相信这些问题非常难以解决——但没有人能保证未来的突破不会破解它们。

最早已知的密码学形式之一是用于替换书写字母的密码。在凯撒大帝的消息中，他将每个字母替换为罗马字母表中三个位置之后的字母。在英语中，这意味着“a”变成“d”，“b”变成“e”，依此类推。要解密来自凯撒的消息，您只需反转该过程，将字母移动三个字母位置即可。

凯撒替换方案有无数种变体——在课堂上传纸条的孩子可以创建自己的方案，用心形替换“a”，用星形替换“b”，依此类推——但它们很容易破解。没收孩子纸条的老师可能会注意到它包含许多孤立的三角形，代表一个字母的单词，并推断出三角形代表“I”或“a”。密码破译者通常可以通过比较不同符号的频率与普通英语文本中字母的频率来解决更复杂的替换方案。

现代密码学的黄金标准，称为高级加密标准或 AES，极大地扩展了凯撒的方法。它通过重复替换条目并像洗扑克牌一样洗牌来打乱消息。经过足够的洗牌和替换后，很难重建原始版本。

要解密消息，您必须通过撤消每次洗牌和替换来解扰消息。对于一副实体扑克牌来说，这几乎是不可能的——洗牌顺序由细微的动作决定。但是计算机根据一组精确的指令（例如，“将第二个条目移动到第五个位置”）对消息进行洗牌，这些指令很容易撤消。计算机只需反向执行指令即可：“将第五个条目移动到第二个位置。”

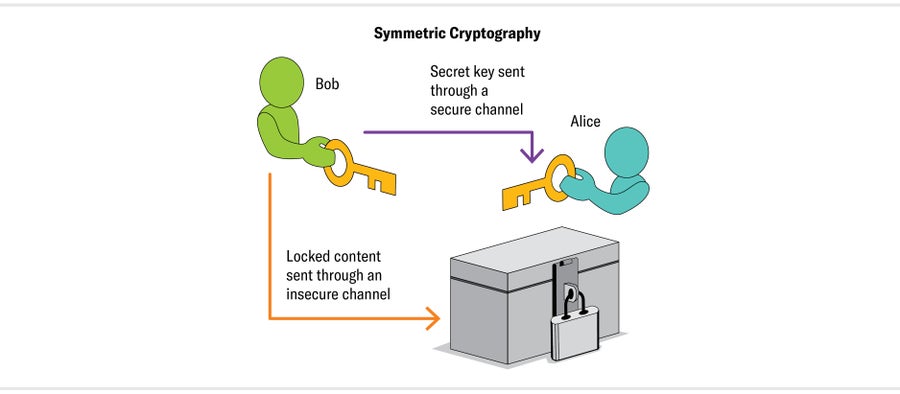
与凯撒密码一样，AES 具有对称的加密和解密程序。它向前和向后应用相同的过程，就像在相反方向转动钥匙来锁定和解锁门一样。在 20 世纪 70 年代之前，所谓的对称密码学（也称为对称密钥密码学）是唯一的密码学类型。但它有一个主要限制：发送者和接收者需要在交换任何消息之前，亲自或通过可信赖的单独通信模式，就加密和解密程序达成一致。

很难想象在没有这种约束的情况下，对称密码学的替代方案。1974 年，加州大学伯克利分校的本科生拉尔夫·默克尔提出了一个课程项目，研究“两个人如何在没有任何事先安排的情况下安全通信”的方法，他预料到这个想法可能显得多么离谱，并补充说，“不，我不是在开玩笑。”默克尔设想了一个系统，两个人完全公开地交换消息，始终假设有人在监听。通过这种公开通信，他们设法建立了一个编码和解码方案，并用它来发送秘密消息。如果其他人正在阅读这些消息，他们将无法弄清楚该方案。默克尔的提案因其“不切实际的工作假设”而被一位专家拒绝。

然而，值得注意的是，几篇数学论文在几年后就实现了默克尔的愿景。提出的两种算法，称为 Diffie-Hellman 和 RSA（Rivest-Shamir-Adleman 的缩写，其创建者的姓氏），在现代通信中无处不在。事实证明，甚至在默克尔的课程项目之前，英国情报组织的研究人员就已经发现了这种编码——公钥密码学——并将其保密。

当您在线查看您的银行账户时，您的计算机和银行的服务器正在交换消息：您发送您的密码，银行发送您的余额。当这些信息在互联网上传输时，其他人可能会读取它。消息需要加密。

大多数消息都使用对称密码学（例如 AES）进行加密，这种密码学可以快速有效地打乱消息。但首先，您的计算机和通信服务器需要就特定的打乱程序达成一致。他们不能简单地写下来，因为他们的所有通信都可能被窃听者捕获。他们需要使用公钥密码学。

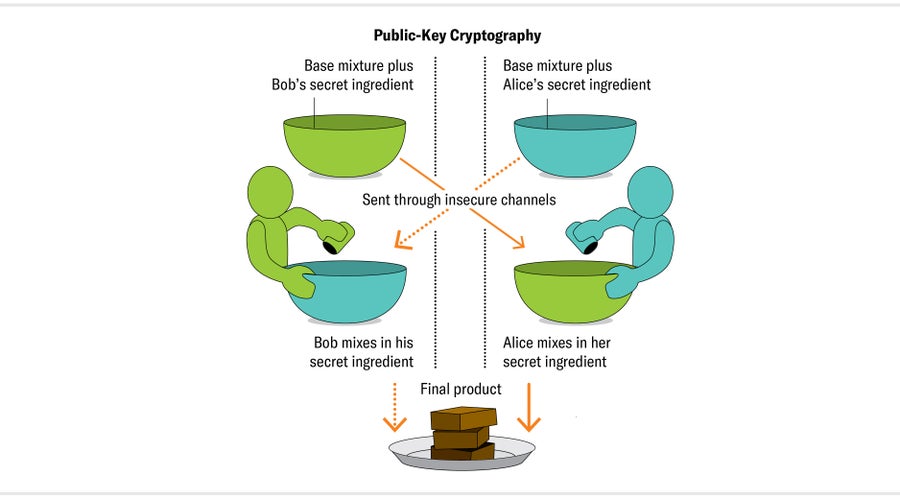
为了理解这个过程是如何工作的，让我们想象一下，两个朋友，爱丽丝和鲍勃，拥有一家面包店，里面有一个绝密的布朗尼食谱。这个食谱非常秘密，甚至爱丽丝和鲍勃也不知道完整的食谱。他们每个人都添加一种只有添加者才知道的特殊成分。为了制作布朗尼，爱丽丝和鲍勃轮流开始食谱。有时，爱丽丝将基本成分与她的秘密成分混合在一起，然后将面糊发送给鲍勃，鲍勃添加他的秘密成分并烘烤。有时，鲍勃先将基本成分与他的秘密成分混合在一起，然后再运送给爱丽丝，爱丽丝混合她的秘密成分并烘烤布朗尼。

爱丽丝和鲍勃总是得到相同的布朗尼——但他们从不与任何人（包括彼此）分享完整、确切的成分。即使是他们狡猾的送货司机伊芙也无法弄清楚食谱。（在密码学中，交换秘密的两个人传统上被命名为爱丽丝和鲍勃，而潜在的间谍通常被命名为伊芙。）伊芙无法推断出秘密成分，因为无论何时她运输它们，它们都与所有基本成分混合在一起——不可能将它们分开。

当然，计算机不烤布朗尼。它们处理数字和数学。在真正的公钥密码学中，目标是最终得到一个共享的秘密数字——类似于授予访问私人对话权限的临时密码。然后，两台计算机可以继续使用对称密码学（例如 AES）进行加密对话。

不同类型的公钥密码学以不同的方式创建和共享临时密码。爱丽丝和鲍勃通过在运输前混合成分来向伊芙隐藏他们的布朗尼食谱。实施公钥密码学的人将改为使用数学函数来混合秘密数字。

函数就像机器，可以接收数字，搅动它们并吐出一个新数字。公钥密码学中使用的函数非常特殊。它们需要在轻松混合数字的同时，使其非常难以解混合。即使伊芙看到了函数的输出，她也不应该能够猜出哪些秘密数字作为输入。

例如，RSA 密码学基于乘法函数及其相反的运算，即因式分解。即使数字非常大，计算机也很容易通过将数字相乘来混合数字。但是，如果数字很大，则撤消乘法运算或因式分解非常困难。（因式分解意味着回答问题：我必须将哪些数字相乘才能得到这个数字？例如，因式分解 21 会得到 3 和 7。）解密使用 RSA 创建的密码需要因式分解一个大数字。最好的方法是过滤许多数字以找到它们的特定组合——这需要计算机很长时间。

哈佛大学的计算机科学家博阿兹·巴拉克说：“我们实际上已经转向基于非常非常简单的东西（如整数因式分解）的密码学，而不是试图使密码学方案越来越复杂，而整数因式分解已经被研究了数千年。”

1994 年，应用数学家彼得·肖尔，时任贝尔实验室的研究科学家，发现了一种方法，量子计算机可以通过这种方法破解使用 RSA 或 Diffie-Hellman 加密的任何代码。正如肖尔告诉我的那样，他参加了一个关于使用量子计算机解决具有周期性或重复结构的数学问题的讲座。这让他想起了“离散对数”问题。对数函数是指数函数的逆函数——例如，在方程 2^x = 16 中找到 x。

通常很容易找到对数，但离散对数问题是关于使用替代算术形式计算对数，在这种形式中，人们像在时钟上一样在一个圆圈中计数。正如 RSA 基于因式分解一样，Diffie-Hellman 基于离散对数问题。计算机科学家普遍认为，使用经典计算机没有快速找到离散对数的方法。但是肖尔找到了一种在量子计算机上做到这一点的方法。然后，他应用类似的逻辑来展示如何使用量子计算机快速分解大数字。这些解决方案合起来被称为肖尔算法。

肖尔并没有想象要编程一台真正的量子计算机——他只是在黑板和纸上做数学。“当时，量子计算机似乎还遥遥无期，”肖尔说。“所以我主要认为这是一个非常好的数学定理。”但他的算法对公钥密码学具有重大意义。量子计算机可以使用它来破解目前使用的大多数密码系统。

经典计算机运行在称为比特的长字符串 0 和 1 上，但量子计算机使用量子比特，它是“量子”和“比特”的混合词。量子比特可以处于叠加态——0 和 1 的奇异组合。通过在两种状态之间徘徊，量子比特使量子计算机能够比经典计算机更快地执行某些任务。但量子计算机很挑剔。量子比特需要在算法运行时保持叠加态，但它们倾向于“坍缩”成 0 和 1 的字符串。

量子计算机看起来令人印象深刻——它们像巨大的金色枝形吊灯一样从天花板上垂下来——但它们仍然不是很强大。科学家们已经能够使用少量的量子比特运行计算，并且他们使用肖尔算法在量子计算机上分解的最大数字是 21。2012 年，英国布里斯托尔大学的研究人员使用量子计算机推断出 21 是 3 乘以 7。

许多专家认为，足够大的量子计算机来破解 RSA 和 Diffie-Hellman 将在未来几十年内建成，但他们很快承认时间表是不确定的。对于需要抢在量子计算机之前的密码学家来说，这种不确定性令人担忧。“每个行业都有其工作的某些方面，这对他们来说非常重要，”IBM 的雷·哈里香卡尔说。医疗保健公司需要保护他们在医学研究中使用的数据，电力公司必须保护电网免受黑客攻击。“最坏的情况：如果发生不好的事情，他们将完全暴露，”哈里香卡尔说。

每种类型的公钥密码学都基于一个难解的数学问题。为了保护秘密免受量子未来的影响，研究人员需要使用非常难解的问题，即使是量子计算机也无法在合理的时间内解决这些问题。NIST 挑战赛征集了公钥密码算法的提名，这些算法可以广泛地在标准计算机上实施，作为 RSA 和 Diffie-Hellman 的替代方案。人们使用的许多不同的连接系统和设备都必须“相互交流这种新型密码学”，NIST 的数学家莉莉·陈说。

在 2017 年的截止日期之前，研究人员提交了 82 种不同的后量子密码学提案。（令人困惑的是，“量子密码学”指的是其他东西——使用量子现象作为安全方案的一部分。）在接下来的一年里，研究人员测试了这些算法，然后 NIST 专家选择了 26 种算法进入下一轮。

公众意见是 NIST 竞赛的重要组成部分。密码系统不能保证安全，因此研究人员试图找出其中的漏洞。候选算法之一使用了“基于同源”的密码学，这种密码学已经研究了十年，看起来很有希望。但两位研究人员注意到，一个 25 年前的数学定理可以用来破解该算法。他们仅用一台标准笔记本电脑就花费了一个小时。

NIST 专家最终确定了几种最终候选算法，其中大多数基于格数学。“格是一种自然的选择，”IBM 的瓦迪姆·柳巴舍夫斯基说，他是 CRYSTALS-Kyber 的作者之一。“人们已经在各种伪装下研究这个问题超过二十年了。”

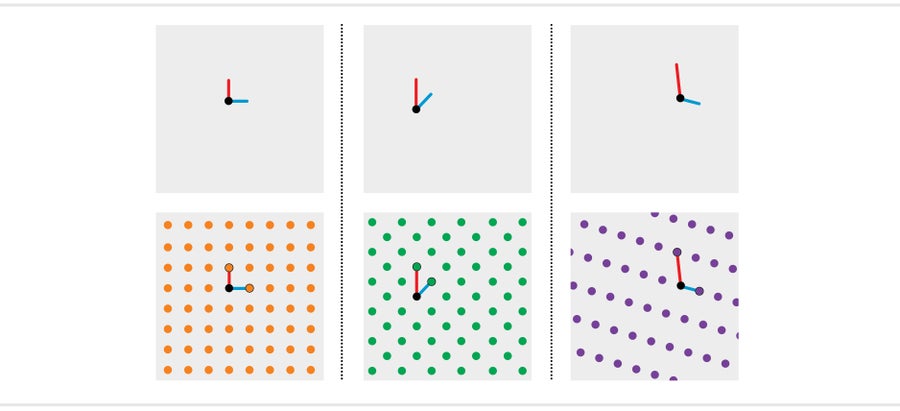
格是点的重复阵列。最简单的一种看起来像钉板——点排列成正方形网格。数学家认为这个格是由两条基本线构成的：一条垂直线和一条长度相等的水平线。想象一下在一张纸的中心画一个点，画一系列垂直或水平线，所有线都等长，从中心向外延伸，并标记线链末端的点。如果您对所有可能的链重复这些步骤，这些点将形成一个正方形网格。不同的初始线集创建不同的格。这两条线的长度可能不相等，或者它们可能不是完全水平或垂直的，而是可以倾斜一定的角度。绘制此类线的链仍然会产生重复的点模式，但行和列会偏移或高度不同。

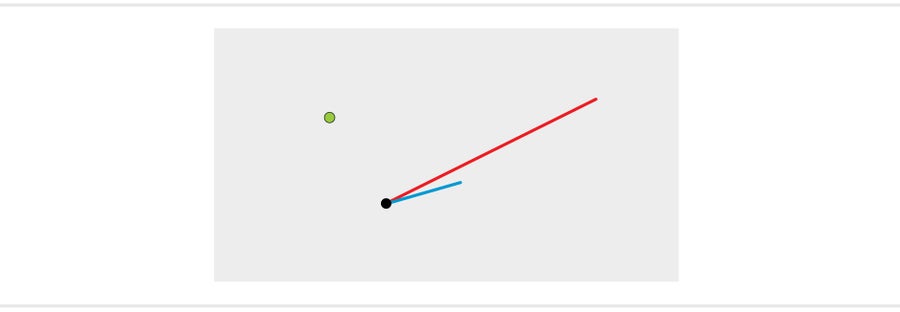
格是一些看似棘手的数学问题的背景。假设我在一张纸上画两条线，并告诉您它们是格的构建块。然后我在页面上的某个地方画一个点。您能找到最接近该点的格点吗？

您可能可以使用基本线开始绘制格点，并最终找到最接近的点。但这只有在纸上的格是二维的情况下才有可能。我们的视觉想象力通常仅限于三维，但数学家可以描述数百维的格。在这些维度中，很难找到最近的格点。

研究人员使用这种巨大的格来构建密码系统。例如，从一个 1,000 维的格开始。从这片点海中，选择一个点。这个点的精确位置代表秘密消息。然后在这个点附近稍微晃动一下，漂离格进入周围空间。您可以公开共享新位置，而无需泄露秘密点的位置——找到附近的格点是一个非常难解的数学问题。就像混合成分保护布朗尼食谱一样，晃动远离秘密点会模糊其精确位置。

计算机科学家已经研究这些问题数十年，并且相当确信它们非常难以解决。但在设计新算法时，密码学家需要在安全性与许多其他考虑因素之间取得平衡，例如两台计算机需要交换的信息量以及加密和解密消息所需的计算难度。在这方面，基于格的密码学表现出色。“格符合这个适中的位置，一切都合理——没有太糟糕的，也没有太好的，”佩克特说。“这有点像金发姑娘。”

问题是，没有人能保证基于格的密码学永远安全。为了防止数学突破解决底层问题——并破解代码——密码学家需要访问各种算法类型。但 NIST 流程中四个最终候选算法中有三个是基于格的算法。在通用公钥加密类别中选择标准化的唯一算法是 CRYSTALS-Kyber。

NIST 竞赛还设有数字签名算法类别，该类别提供有关谁发送了消息以及消息未被修改的保证。加密算法回答了“我知道没有人会阅读这个吗？”这个问题，加利福尼亚州蒙特雷海军研究生院的密码学家布里塔·黑尔解释说，而数字签名回答了“我可以相信这些数据没有被修改吗？”这个问题。目前使用的数字签名算法也容易受到肖尔算法的攻击。NIST 选择标准化三种数字签名算法，其中两种是基于格的算法。

如此严重地依赖单一类型的数学问题是有风险的。没有人能确定数学家最终不会破解它。它也没有给用户任何灵活性——可能会发现另一种类型的密码学更适合他们的特定需求。出于这些原因，NIST 扩展了这两个类别的标准化过程，以研究非基于格的算法。“我们的目标不是依赖任何一个数学族来选择算法，”NIST 的数学家达斯汀·穆迪解释说。

即使是已经选择标准化的算法也需要在过程中进行调整。在第一轮提交后，研究人员注意到 CRYSTALS-Kyber 存在一个小问题，作者解决了这个问题。在竞赛的后期，他们找到了一种稍微改进算法的方法。“我们更改了参数以获得更多的安全比特，”德国波鸿马克斯·普朗克安全与隐私研究所的彼得·施瓦布说，他是 CRYSTALS-Kyber 的创建者之一。

NIST 现在正处于制定标准的阶段，标准详细描述了计算机程序员应如何逐步实施算法。“互联网上的一切都必须有非常具体、非常枯燥的标准，包含每一个小细节。否则计算机就无法相互通信，”柳巴舍夫斯基说。标准制定后，每个计算机系统都需要切换到后量子密码学。不会有所有人同时拨动开关的那一刻。各个软件公司需要升级他们的协议，政府需要更改他们的要求，物理硬件设备需要更换。

完全过渡到后量子密码学可能需要很多年，甚至几十年。在此之前，使用旧形式密码学发送的任何消息都可能被未来的量子计算机读取。根据您希望保守秘密的时间长短，担忧的时间可能已经过去。正如黑尔所说，“在密码学方面，每个人都在看表，说，‘你们已经过期了。’”