有时你的直觉会误导你——尤其是在数学中,你经常会遇到看似不可能的结果。例如,无穷大并非总是等于无穷大,而乌龟可能超越人类运动员——至少从某种数学角度来看是这样。
还有许多乍一看(或第二眼或第三眼)似乎自相矛盾的情况。然而,这些悖论是可以解释的。它们不是错误,而是提醒我们不应在数学中过分依赖直觉。以下是该领域中最奇怪的三个悖论。
希尔伯特旅馆
支持科学新闻报道
如果您喜欢这篇文章,请考虑订阅以支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事能够拥有未来。
想象一下,您正在前往一个城市旅行,却忘记提前预订房间。幸运的是,您偶然发现一家以著名数学家大卫·希尔伯特命名的美丽酒店,您非常欣赏他的工作。您走到接待处,看到这家酒店有无限数量的房间:房间号对应于自然数 1、2、3、4,...,永无止境。
然而,接待员告诉您酒店已满。但您精通数学,所以不会轻易被敷衍了事。您知道一个技巧,可以让您以及所有其他无数的客人也找到房间。您向接待员建议,让每位客人搬到房间号比他们当前住宿房间号大一号的房间。因此,1 号房间的人搬到 2 号房间,2 号房间的人搬到 3 号房间,依此类推。
因为希尔伯特旅馆拥有无限数量的可用房间,即使客满,仍然有空间容纳更多客人。而且这不仅仅适用于一个人:他们可以带一整车也想要房间的人。在这种情况下,酒店客人必须搬到房间号不止大一号的房间。
更奇怪的是。即使您带无限数量的人来到希尔伯特旅馆,您仍然可以在客满的酒店中容纳他们。为此,1 号房间的客人必须搬到 2 号房间,2 号房间的客人搬到 4 号房间,3 号房间的客人搬到 6 号房间,依此类推。当每个人都搬到房间号是他们当前房间号两倍的房间时,无限数量的奇数房间就空出来了。
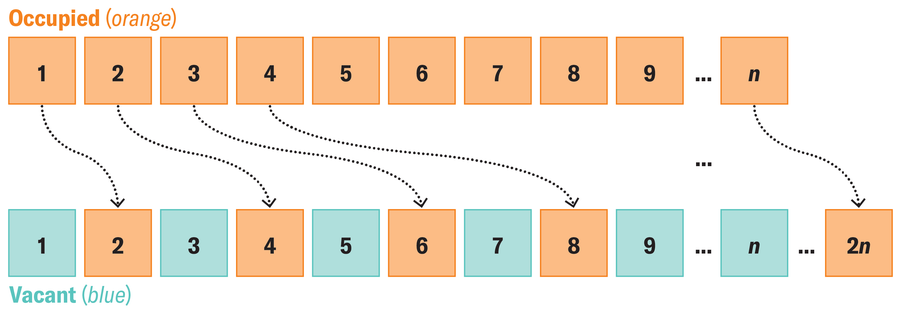
通过将每位客人移到房间号是他们当前房间号两倍的房间中,就有空间容纳无限数量的额外人员。
Jan Beránek/维基共享资源 (CC BY-SA 4.0),由阿曼达·蒙塔内斯重新设计
德国数学家大卫·希尔伯特在 1925 年关于无穷大的讲座中提出了这个所谓的悖论。这个例子说明了并非所有概念都可以从有限情况转移到无限情况:“每个房间都住满了”和“酒店不能再接待更多客人”这两个陈述在现实世界中是同义的——但在一个拥有无穷大的世界中则不然。
生日悖论
下一个悖论对许多人来说更熟悉。当我在学校时,我的几个同学在同一天过生日的情况并不少见。事实上,我也和一个同学同一天生日。乍一看,这似乎是一个巨大的巧合。毕竟,一年有 365 天(闰年有 366 天,但为了简单起见,我们忽略这一点),一个班级大约有 20 到 30 名学生。因此,我们的直觉告诉我们,两个孩子在同一天出生的可能性不大。
但事实并非如此。事实上,在 23 人一组中,有两人在同一天过生日的概率超过 50%。为了更好地理解这一点,最好不要看人数,而是看人与人之间的对数。从 23 个人中,可以形成 (23 x 22) / 2 = 253 对——这个数字超过了一年中天数的一半。如果我们看一下一个 23 人的班级中,有一个学生在特定日期出生的概率,那么这个概率只有 1- ((365-1) /365)^23=6.1%。
因此,生日悖论的产生是由于查看学生对会比只看个人给出更多的可能性。
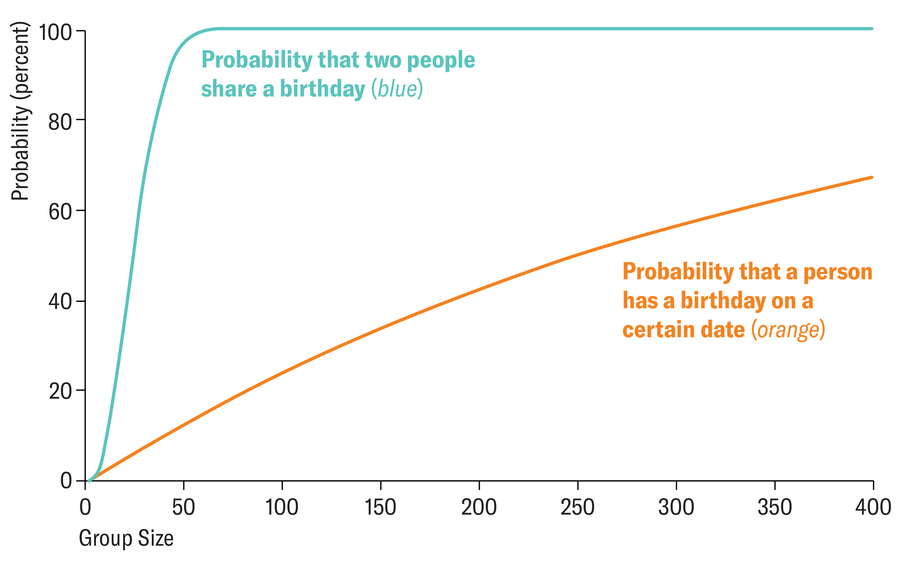
蓝线表示一组人(x 轴上标明了组的大小)中有两人生日相同的概率。橙线对应于一个人在特定日期过生日的概率。
Toobaz/维基共享资源 (CC BY-SA 4.0),由阿曼达·蒙塔内斯重新设计
这个事实在密码学中具有实际效果。例如,如果您想签署一份数字合同,则会使用“哈希函数”:当文档被签署时,它会被转换为固定长度的字符串(“哈希”)。即使对原始文档进行最小的更改,从中形成的哈希也会完全不同。通过保留他们的哈希,签名者可以证明他们最初签署的内容——使该过程具有防篡改性。然而,两个完全不同的文档会生成同一个哈希的可能性极低,这会带来安全风险。
通常,哈希函数的长度被选择为使得这种“冲突”(两个不同的数据记录产生相同的哈希)极为罕见。然而,黑客可以进行“生日攻击”:他们可以生成许多不同的文档,并将它们的哈希函数成对比较——就像老师比较同学的生日而不是关注特定日期和单个学生一样。
在实践中,生日攻击可能是这样的:我首先创建两个合同,V1 和 V2。V1 是一份公平的合同,但 V2 的措辞对我有好处。然后我在两个合同的各个地方进行更改:我添加空格、制表符和换行符以创建 V1 和 V2 的变体。这些更改对于读者来说几乎是不可见的,但它们会彻底改变文档的哈希函数。
如果我成对比较修改后的合同 V1 和 V2 的各个哈希函数,我会比专门尝试重现特定哈希(例如 V1 的哈希)更快地找到匹配的哈希。如果我找到一对匹配的 V′1 和 V′2,我可以给您合同 V′1 签名,但在事后声称您签署了 V′2。因为两者生成相同的哈希,所以数字签名软件无法检测到欺诈行为。
罗素悖论
英国哲学家伯特兰·罗素在 1901 年提出了一个悖论,有时称为罗素悖论——一个描述两个看似矛盾的想法的术语。与希尔伯特旅馆和生日悖论不同,罗素悖论不仅仅是一个逃脱我们直觉的结果。它本身就违反了逻辑规则。该悖论产生既非假亦非真的陈述。
有几个例子可以说明罗素悖论,但一个著名的例子是“理发师悖论”。假设一位理发师为镇上所有不给自己刮胡子的人刮胡子——并且只为这些人刮胡子。理发师给自己刮胡子吗?如果他给自己刮胡子,那么他就不再属于不给自己刮胡子的人群。但如果他不给自己刮胡子,那么根据定义,他就必须给自己刮胡子(因为所有不给自己刮胡子的居民都会去找他)。
这个问题是由于集合定义不明确而引起的。在罗素提出悖论的时候,集合通常指的是事物的集合:例如,自然数形成一个集合,所有不给自己刮胡子的居民的集合也是如此。这也允许集合包含自身或将自身作为一个整体来引用——而这些属性会导致矛盾。因此,这个悖论导致了数学家所称的“朴素集合论”的终结。
数学的基础仍然依赖于集合论。但是,这种结构中的集合不再仅仅是集合,而必须满足某些条件。例如,集合必须由已存在的集合组成,并且不得引用自身。这排除了诸如理发师悖论之类的悖论。
用数学符号表示:镇上可以长胡须的男性构成集合 M。该集合包括给自己刮胡子的男性和不给自己刮胡子的男性。接下来,集合 C 包括理发师的所有顾客。要形成 C,您必须遵循现代集合论的规则:如果理发师是一个有胡须的男人,或者 M 的一部分,那么顾客集合就不能定义为“所有不给自己刮胡子的男性居民”——因为在这种情况下,定义会引用自身,理发师和顾客都是 M 的一部分。集合论根本不允许这样的定义。但是,如果理发师不是 M 的一部分——例如,如果理发师是女性或无法长出胡须——那么这个定义是被允许的。
我们现在可以松一口气了:悖论已经解决,数学并没有注定失败。然而,不能保证数学规则在某个时候不会产生无法解决的矛盾。逻辑学家库尔特·哥德尔在 20 世纪 30 年代证明了这一点——并且这样做清楚地表明,不能确定数学将永远以自洽的方式运作。我们能做的最好的事情是希望永远不会出现无法解决的矛盾。
本文最初发表在《科学世界》杂志上,经许可转载。
