你能想象到的最奇异的实数是什么?可能很多人会想到像 pi (π) 或欧拉数这样的无理数。事实上,这些值可以被认为是“狂野的”。毕竟,它们的十进制表示是无限的,没有数字会重复。然而,即使是这些看起来很疯狂的数字,连同所有有理数,也仅占实数(或可以出现在数轴上的数字)的一小部分。(提醒一下,这些是可以用于各种常见测量的数字类型,包括时间、温度和距离。)
但事实证明,如果你碰巧在数轴上随机选择一个数字,你几乎肯定会抽到一个“不可计算”的数字。对于这样的值,没有办法精确地确定它们。
实数由有理数和无理数组成。有理数(即可写成p⁄q分数的数,其中p和q是整数)包括自然数(0、1、2、3...)和整数(...、–2、–1、0、1、2...)。数轴上的其余数字是无理数。这些数字也可以分为不同的类别——其中大多数是我们甚至无法想象的。
支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保关于塑造我们今天世界的发现和想法的具有影响力的故事的未来。
无穷大、无穷小、虚数或其他不寻常的数字空间可能难以描述,这似乎并不太令人惊讶。但人们会认为我们现在可以完全理解描述我们世界中距离的实数。不幸的是,事情并非那么简单。要理解这一点,我们必须仔细研究无理数。
什么是无理数?
所有不能表示为两个整数之比的实数都是无理数。(提醒:整数是整数。)无理数包括,例如,2 的平方根,其十进制表示是无限的,且永不重复。事实上,√2 是最简单的无理数之一,因为它是可构造的——也就是说,它可以通过使用圆规和直尺绘制两条边长为 1 个单位的直角三角形来生成。那么该三角形的斜边长度为 √2。以类似的方式,黄金比例 φ 可以几何构造,许多其他无理数值也可以。
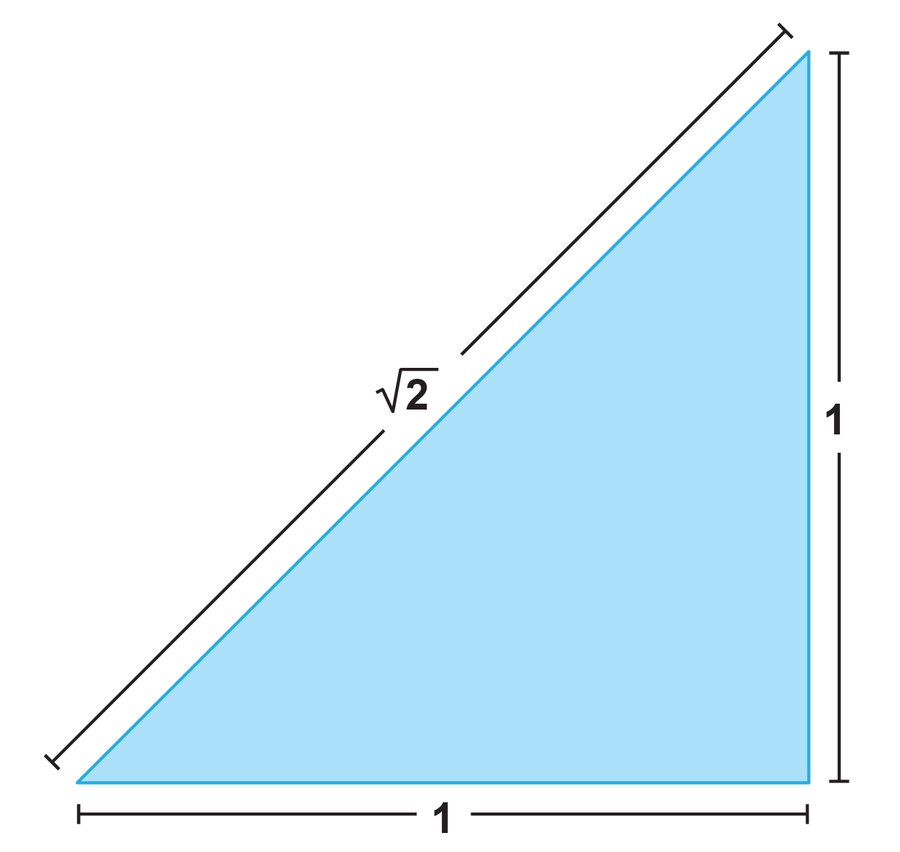
通过创建一个两条边长为 1 的直角三角形,可以几何构造 2 的平方根。剩余边的长度将为 2 的平方根。图片来源:Rubber Duck/ Pbroks13/Wikimedia Commons,由大众科学设计
然而,即使在古代,人们也遇到了无法以如此简单的几何方式生成的数字。一个著名的例子是立方倍积问题:如何将边长为 1 的立方体构造为体积是其两倍的立方体?正如数学家皮埃尔·万策尔在 1837 年发现的那样,这个新立方体所需的边长 ∛2 无法使用圆规和直尺构造。但是 ∛2 属于代数数,它可以写成多项式方程的解。对于 ∛2,相应的方程是 x3 = 2。
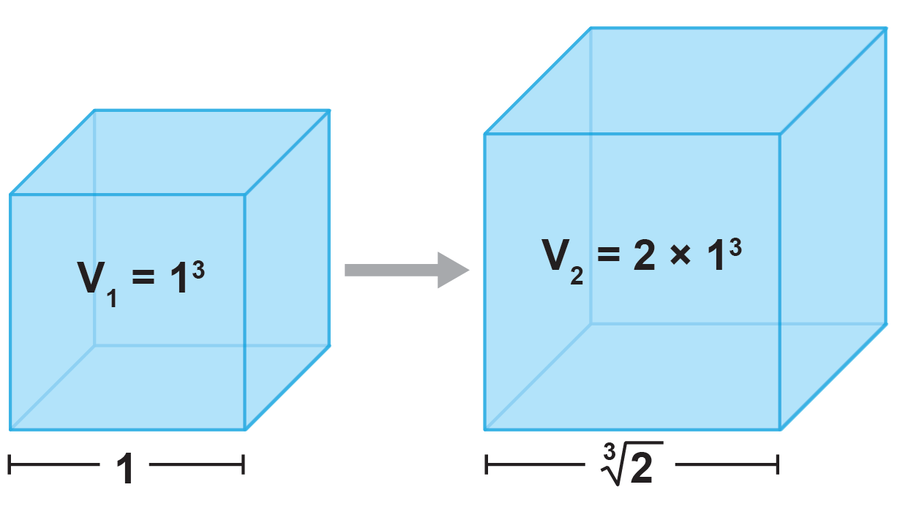
有些无理数无法通过几何方式构造。例如,一个边长为 1 的立方体,如果不使用多项式方程(即 2 的立方根)来表示体积,就无法将体积翻倍。图片来源:Petrus3743/Wikimedia Commons (CC BY-SA 4.0),由大众科学设计
有些数字是超越数
还有一些超越数,它们不能表示为这种方程的解。也就是说,没有简单的公式可以计算它们。著名的 π 就属于这一类。但这并不意味着我们不知道它的值。希腊数学家阿基米德发现了一个计算规则来确定 π,至少是近似值。此外,还有许多算法可以随意吐出 π 的第 5.87 亿位小数。在足够的计算能力和时间下,至少在理论上,这个数字可以被确定到任意精度。欧拉数 (e) 或 2√2 也同样适用。
超越数蕴藏着许多谜团。虽然有明确的方法来判断一个数是否是可构造的,但相比之下,证明一个值是否是超越数却很困难。例如,在 1934 年,苏联数学家亚历山大·盖尔丰德成功证明复合数 eπ 是超越数。但是,πe 或 π x e 或 π – e 的值是代数数还是超越数,至今仍不清楚。
不可计算数更加奇怪
直到 20 世纪初,人们还认为超越数是实数所能提供的最疯狂的东西。但这是错误的。1937 年,英国数学家艾伦·图灵发表了一篇关于可计算数的论文。他用这个术语来描述所有那些存在计算规则(即算法)的值,计算机可以执行该规则来计算任意精度的数值。
几乎所有已知的超越数,例如 π 和 e,都属于这一类。毕竟,我们至少知道它们的近似数值,以及如何计算它们。然而,正如图灵在他的工作中表明的那样,也存在同样不可计算的数字,其值无法以任意精度逼近——也就是说,我们不知道它们是什么样子。
更糟糕的是:几乎所有实数都是不可计算的。
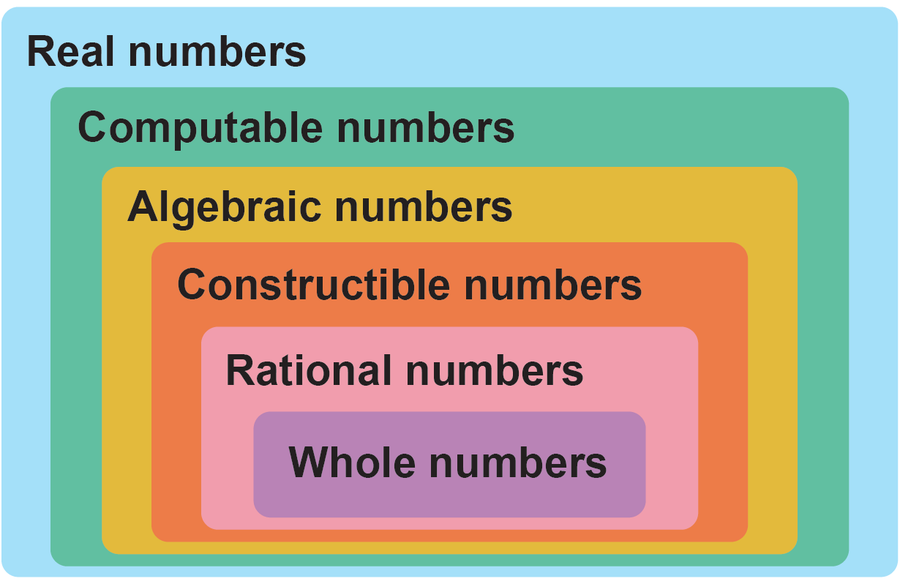
实数包括可计算数、代数数、可构造数、有理数和整数。图片来源:Spektrum der Wissenschaft/马农·比肖夫,由大众科学设计
如果思考不同数集的无限大小,就会认识到这一点。数学家格奥尔格·康托尔在 19 世纪末为这个想法奠定了基础。当时,他能够证明,例如,自然数、整数和有理数的集合具有相同的基数(集合大小的数学表达式)。为什么会这样?要理解这一点,首先应该注意到,有限数的相同计算规则不适用于无穷大。以自然数和整数为例:可以将一个正整数和一个负整数交替分配给每个自然数,例如 (0, 0)、(1, –1)、(2, 1)、(3, –2)、(4, 2),等等。由于自然数没有尽头,因此我们找到了两个集合之间的一一映射。这就像在公共汽车站为每个人分配一个座位,反之亦然。在这种情况下,我们知道公共汽车上的座位和公共汽车站的人数一样多。自然数和整数也是如此。
在有理数和自然数之间可以找到类似的一一映射。正如康托尔能够证明的那样,自然数的基数是最小的可能无穷大。他称之为“可数无限”。
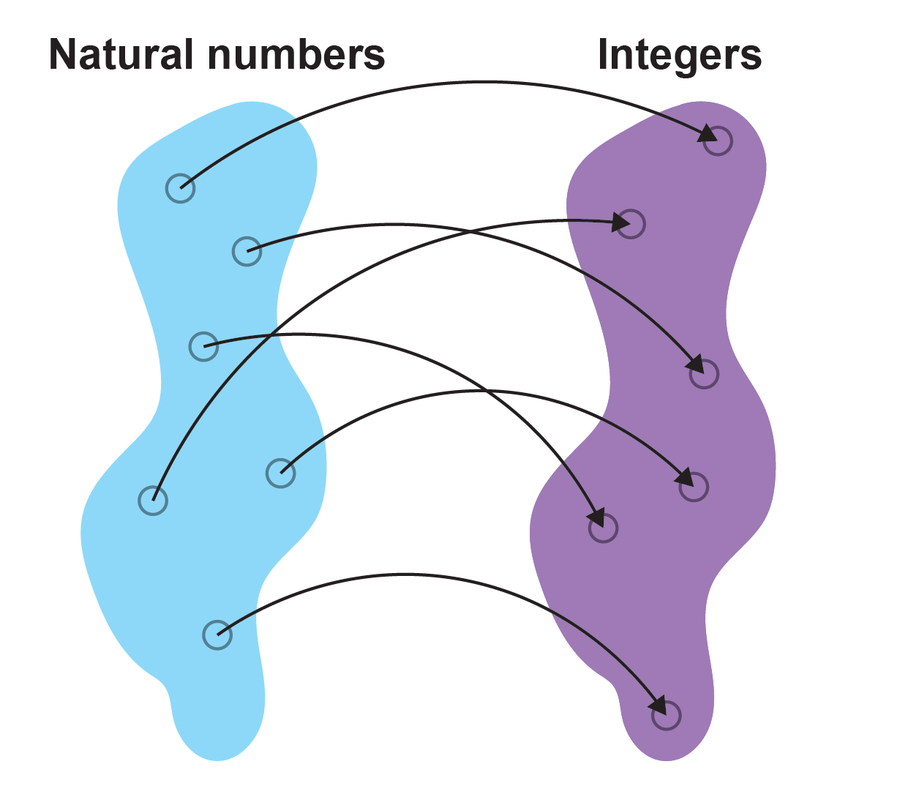
如果各个集合的元素之间存在一一映射,则两个集合相等。图片来源:Spektrum der Wissenschaft/马农·比肖夫,由大众科学设计
另一方面,实数是不可数的。康托尔能够证明,实数的基数必然大于自然数的基数。他通过证明,无论列表有多长,都无法列举所有实数而不遗漏某些值。因此,实数构成一个不可数集。
康托尔的推理如下:假设有一个包含所有实数的列表。那么可以将此列表想象成一个表格。在每一行中,都有一个数字,每一列都为小数点位置提供一个位置。康托尔证明,如果在该表格中围绕一组形成对角线的数字(例如,第一行中的第一位数字,第二行中的第二位数字等)画一个圆圈,则可以通过将 1 添加到每个对角线条目来创建一个新的实数。这个新数字不能包含在列表中。因此,您最初的所有实数列表是不完整的。
但是正如图灵所说,所有可计算数都必须是可数的。对于这些数字中的每一个,都可以开发一台机器,该机器只需计算其值即可。由于可以对这些计算机器进行编号,因此可计算数必然是可数的。反过来,这导致不可计算数在绝大多数实数中占主导地位:它们的数量是不可数的!
因此,如果你计算随机抽取一个实数时会遇到哪种实数的概率,你将得到一个明确的结果:在 100% 的情况下,这个数字将是不可计算的。但这并不意味着你不能抽取任何其他数字。对于无限组事件,概率为零并不意味着结果是不可能的。
考虑到我们知道的可计算数的丰富性,不可计算数如此丰富这一事实更加令人惊讶,
停机问题作为灵感
少数现有的不可计算数示例是由计算机科学中著名的停机问题定义的。要思考这个问题(由图灵提出),请想象一台计算机执行一组特定的指令以解决问题(换句话说,计算机正在使用算法)。在停机问题中,要求您想象一台机器,它可以判断运行给定算法的计算机是否会在某个时候停止,还是会永远继续下去。正如图灵所证明的那样,虽然这样一台机器可以判断某些算法是否可以在有限时间内执行,但显然没有一种方法可以对所有可能的程序代码执行此操作。停机问题是数学家的直接应用
库尔特·哥德尔不完备性定理,该定理指出并非所有数学陈述都可以证明。
阿根廷裔美国数学家格雷戈里·柴廷使用停机问题来定义不可计算数。所谓的柴廷常数 Ω 对应于计算机的理论模型(图灵机)对于任何给定输入停止的概率:Ω = –∑p½|p|,其中 p 表示所有在有限运行时后停止的程序,|p| 描述了程序的长度,单位为比特。
因此,要精确计算柴廷常数,就需要知道哪些程序停止,哪些程序不停止,根据停机问题,这是不可能的。尽管如此,在 2000 年,数学家克里斯蒂安·S·卡卢德和他的同事成功地计算出了柴廷常数的前几位数字:0.0157499939956247687....
这意味着,如果你在卡卢德及其同事使用的语言中随机生成一个程序,它将以大约 1.58% 的概率在有限的运行时间内停止。即使结果具有很高的精度,柴廷常数也无法以任意精度计算。
一个不可计算数和一只忙碌的海狸
另一个不可计算数来自“忙碌的海狸函数”,或 BB(n)。此函数计算算法可以从 n 位产生的最大可能输出(以比特为单位测量)。
例如,不可计算数来自以下构造:∑n½BB(n)。到目前为止,只知道忙碌的海狸函数的前四个值。至少可以估计另外两个值。
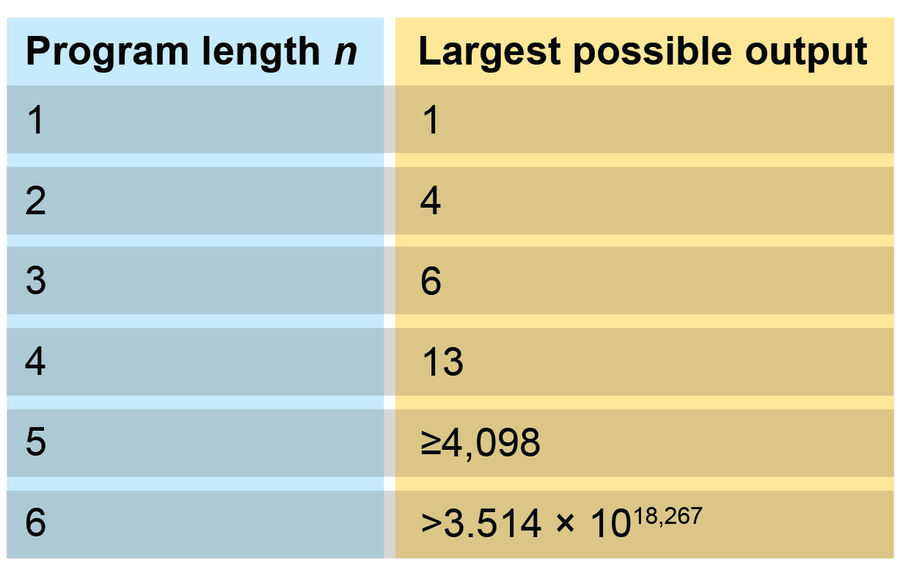
忙碌的海狸函数计算算法可以从给定数量 (n) 的比特产生的最大可能输出(以比特为单位测量)。图片来源:Spektrum der Wissenschaft/马农·比肖夫,由大众科学设计
因此,这个不可计算数的前几位数字是 ∑n½BB(n) = 0.51562548....
还有其他复杂的方法可以定义不可计算数。也许你也可以想出一个变体。尽管如此,鉴于我们知道的可计算数的丰富性,不可计算值主导实数——从而主导我们的世界,这始终令人惊讶。
本文最初发表在《Spektrum der Wissenschaft》杂志上,并经许可转载。
编者注(2023 年 6 月 13 日):本文在发布后进行了编辑,以更正忙碌的海狸函数的图形以及关于随机生成卡卢德及其同事使用的语言的程序时会发生什么情况的描述。