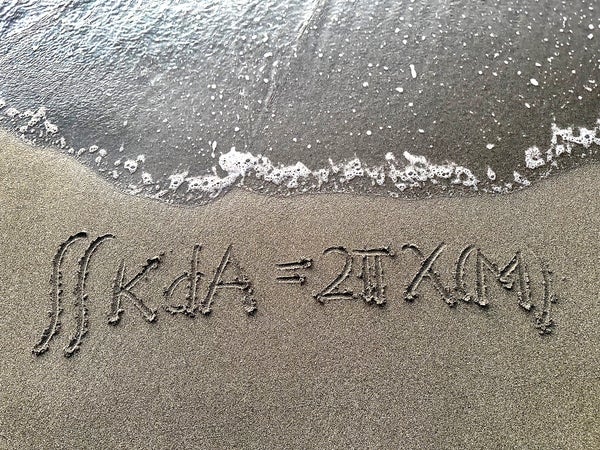对于数学家来说,方程就是艺术。正如许多人会被绘画或音乐所感动一样,对于那些欣赏和理解数学的人来说,数字、变量、运算以及量与量之间关系的表达也同样引人入胜。
正如艺术美一样,数学美也存在于观察者的眼中。一位数学家可能会珍视简单明了、简洁的方程,而另一位数学家可能更喜欢相反的方程。正如有些人喜欢现代艺术,而另一些人则喜欢中世纪作品一样,古代和现代的方程都因其巧妙、强大和可能性而受到赞赏。
以下是一些数学家选择的最美丽的数学方程,以及他们自己关于哪些因素使它们如此精美的看法。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保关于塑造我们今天世界的发现和想法的具有影响力的故事的未来。
洛伊纳微分方程
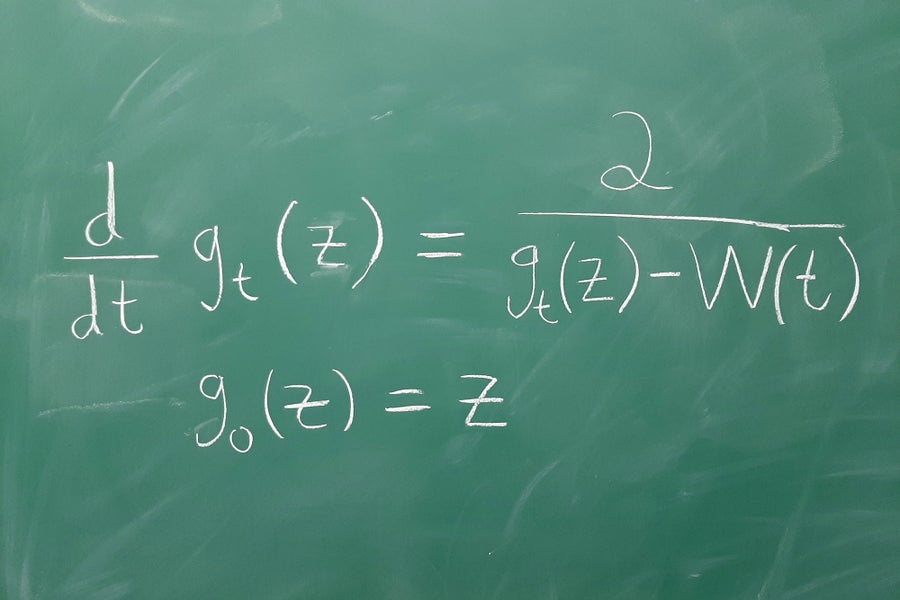
尤恩·格温
有些方程之所以美丽,是因为它们揭示了不同学科之间意想不到的关系。洛伊纳微分方程由查尔斯·洛伊纳于 1923 年提出,描述了定义在复平面子集上的一系列共形(保角)函数的时间演化。该方程的输入是一个连续函数 W(t),称为驱动函数。
近 80 年后的 1999 年,奥德·施拉姆发现,当驱动函数被视为布朗运动(概率论研究的中心对象)时,洛伊纳方程的解具有特殊的对称性。在施拉姆的发现基础上,证明了对于驱动函数的这种选择,洛伊纳方程的解,称为施拉姆-洛伊纳演化,描述了二维统计力学中各种临界模型的大尺度行为。在施拉姆的工作之前,洛伊纳方程在概率论中的这种应用是完全出乎意料的。它彻底改变了统计力学的数学研究,并导致了过去二十年数学领域一些最激动人心的突破。——尤恩·格温,芝加哥大学
高斯-博内方程
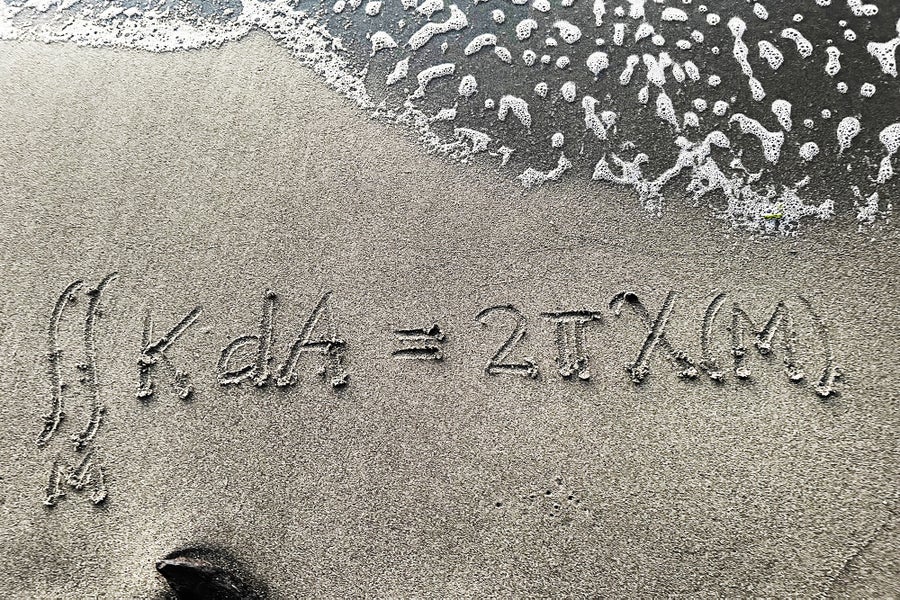
艾拉娜·弗雷泽
高斯-博内公式是微分几何中一个美丽的方程,它断言曲面上高斯曲率的积分等于一个常数乘以曲面的欧拉示性数。这个方程之所以引人注目,是因为它将两个非常不同的量联系起来:一方面是曲面的曲率,另一方面是曲面的拓扑结构。曲面上一点的曲率是该点曲面弯曲程度的度量,或者曲面偏离平面的程度。欧拉示性数是曲面的全局拓扑不变量,它描述了曲面的拓扑结构,而与其弯曲方式无关。这个方程令人惊讶,例如,它意味着如果您连续地变形一个曲面,总曲率将保持不变。高斯-博内方程的各种版本最初由卡尔·弗里德里希·高斯和皮埃尔·奥西恩·博内于 19 世纪上半叶提出,它仍然是几何学中最美丽和最引人注目的方程之一。这个方程的一些美丽之处在于其表达式的简洁性和它所表达的深刻性。 ——艾拉娜·弗雷泽,不列颠哥伦比亚大学
索博列夫不等式
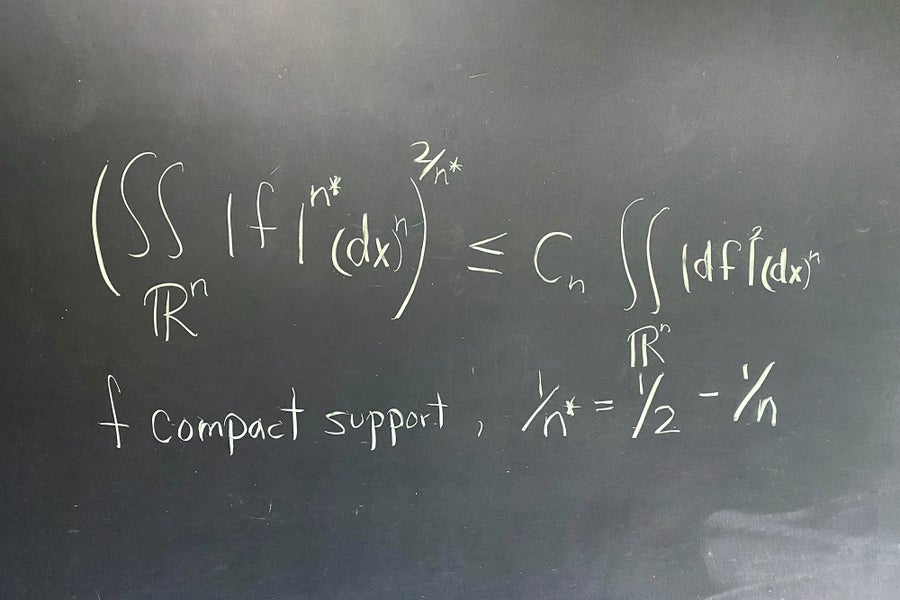
凯伦·乌伦贝克
我喜欢不等式。索博列夫不等式和相关不等式估计了导数项中的函数,构成了我们理解偏微分方程的基础。当 n = 2 时不等式的失败与 n = 2 特有的性质有关。——凯伦·乌伦贝克,普林斯顿高等研究院
黎曼-罗赫等式
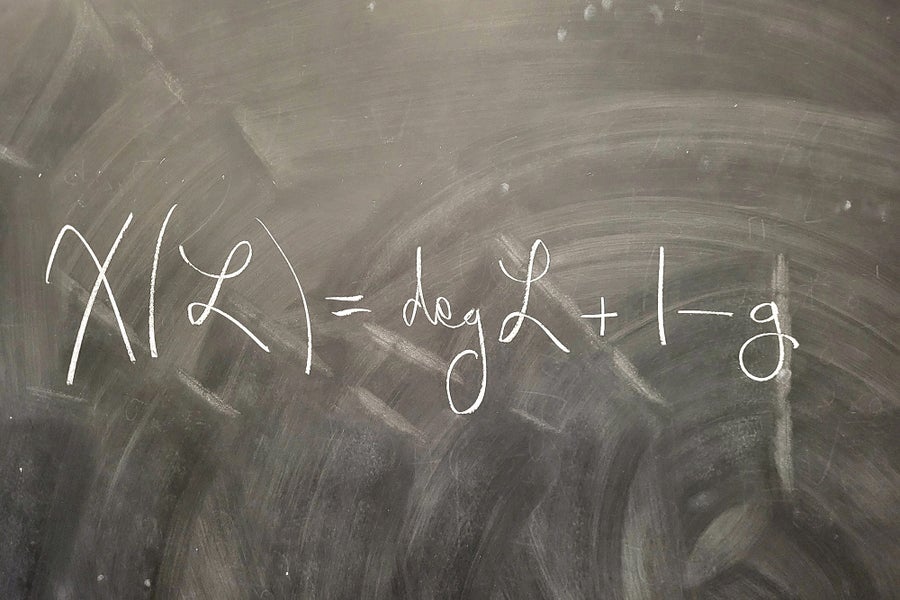
桑多尔·科瓦奇
黎曼曲面是一个紧致可定向曲面。黎曼曲面的区别在于它们容纳的孔或把手的数量。这个数字称为亏格,用 g 表示。例如,亏格 g=0 的黎曼曲面是一个球面,亏格 g=1 的黎曼曲面是一个环面,或甜甜圈。复黎曼曲面是一个具有复结构的黎曼曲面。换句话说,它也是一个复流形。
黎曼曲面上的除子是有限多个点的选择。除子的次数是其中点的数量。它用“deg”表示。先验地,除子仅仅取决于拓扑信息,除子的次数也是如此。然而,一旦黎曼曲面配备了复结构——换句话说,当它被视为复流形时——那么人们可能会问关于该复结构的问题,例如是否存在亚纯函数,其零点或极点与给定的除子一致。这引出了经典米塔-列夫勒问题的一个版本。由复结构确定的最简单的不变量之一是除子的全纯欧拉示性数,它在某种程度上是该特定黎曼曲面上米塔-列夫勒问题的校正项。对于除子 ℒ,其全纯欧拉示性数用 χ(ℒ) 表示。
现在我们准备陈述黎曼-罗赫等式。考虑亏格为 g 的复黎曼曲面以及其上的除子 ℒ。该方程为 χ(ℒ) = degℒ + 1 – g。
这个看似简单的方程具有深远的意义。除其他外,它意味着全纯欧拉示性数仅取决于拓扑信息。
至于是什么使一个方程变得美丽,我想说,我发现那些要么揭示意想不到的东西,要么连接看似无关的不变量的方程很有趣。——桑多尔·科瓦奇,华盛顿大学
分次环之间的同构

大卫·阿亚拉
我发现这个方程很美,因为它新颖且令人惊讶,并且信息显然从右侧项 (RHT) 流向左侧项 (LHT)。事实上,LHT 显然是几何的,而 RHT 纯粹是代数的。此外,由于 RHT 是可计算的,因此该方程给出了流形的分类,这是一项深入研究的企业。最后,这个结果是同类首创,其证明技术促使了数学许多领域中富有创造力的新方法和视角。——大卫·阿亚拉,蒙大拿州立大学
无穷级数
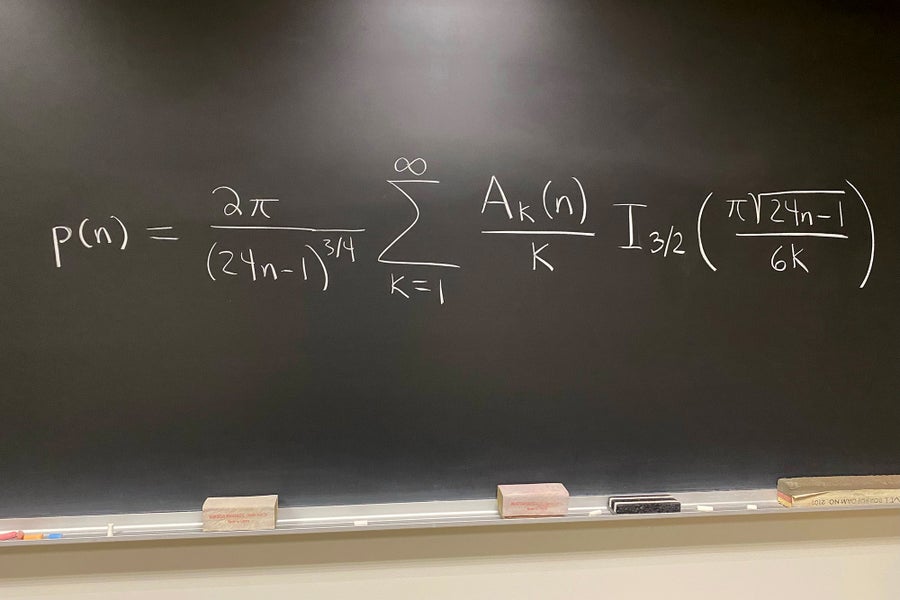
阿曼达·L·福尔瑟姆
我不认为存在一个最美丽的数学方程,但这个方程对我来说很突出。在撰写这篇文章时,我向一个年幼的孩子展示了它的照片。我们首先讨论了方程是什么(一个用等号连接两个事物的数学陈述,例如 4 = 2 + 1 + 1),他们问为什么这个方程这么大。我们讨论了右侧在视觉上是较大的一侧,但左侧不是——右侧是一个和(如 2 + 1 + 1),但有无限多项,而左侧与数论中的整数分拆有关。例如,n = 4 有五个分拆 (4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1),因此在 n = 4 处评估的分拆函数 p(n) 为 5 (p(4) = 5)。
这个重要且看似基本的功能与加法和计数有关,但它非常复杂,这也许是出乎意料的。例如,p(100) 超过 1.9 亿,但可以肯定的是,找出答案的方法不是写出 n = 100 的数百万个分拆并计算有多少个。感谢汉斯·拉德马赫在 1937 年的工作,他扩展了 G. H. 哈代和斯里尼瓦萨·拉马努金的早期相关工作,这个方程的右侧是 p(n) 的精确公式。有些人可能会认为(大的)右侧,一个涉及复(虚)数 (Ak(n))、分数幂(3/4 和平方根)、超越数 pi 等等的无限和,与美丽相反,或者令人望而生畏——特别是考虑到它取代了(视觉上很小的)左侧,即使是孩子也能理解。解析数论以及拉德马赫和哈代以及拉马努金的工作的美丽之处在于,它表明 p(n) 的这个公式是存在的——这本身就是一项壮举——并且事实证明,通过截断无限和并进行四舍五入,它对于计算 p(n) 是实用的。这里出现的无限和收敛,意味着它求和为有限值、一个计算重要事物的实数,并且不会不断累积——更不用说数学遗产、进一步的研究以及与今天仍然存在的其他领域的联系,现在已经接近一个世纪了。——阿曼达·福尔瑟姆,阿默斯特学院
欧拉乘积公式
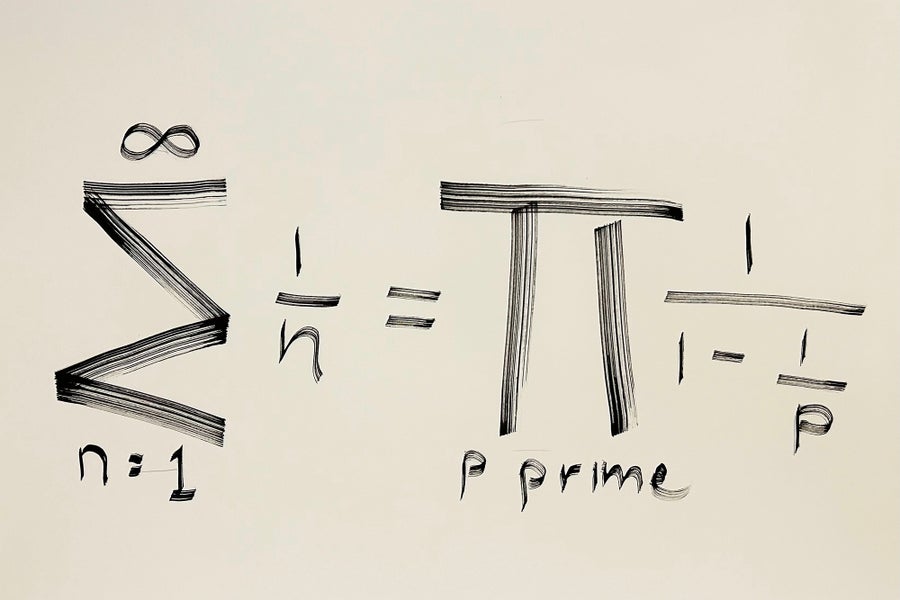
理查德·施瓦茨
很难挑选出数学中最美丽的单个方程,但我认为欧拉乘积公式在任何此类列表中都名列前茅。让我赞扬一下这个公式的优点。首先,它很简单。它只涉及加法、减法、乘法和除法运算。其次,它是基本的:它表达了左侧计数数字和右侧质数之间的深刻关系。第三,它令人惊讶且出乎意料,以一种非常新颖的方式将基本运算交织在一起。第四,它有用且功能强大。仅仅作为一个开始,它就给出了质数无穷性的另一种证明。左侧是一个发散级数。如果只有有限多个质数,则右侧将是有限的,这是一个矛盾。人们还可以从方程中挤出关于质数的更深层信息。例如,人们可以使用欧拉乘积公式来证明质数倒数的和是发散的。这个结果远远超出了欧几里得关于质数无穷性的经典证明。第五,该公式非常流行。它仍然在数论中发挥着重要作用,并且是理解质数分布的关键工具之一,即使在今天也是如此。第六,它是可访问的:它有一个优雅的证明,使用了整数可以唯一分解的事实,以及几何级数的简洁性质。——理查德·施瓦茨,布朗大学
赖芬贝格平坦集
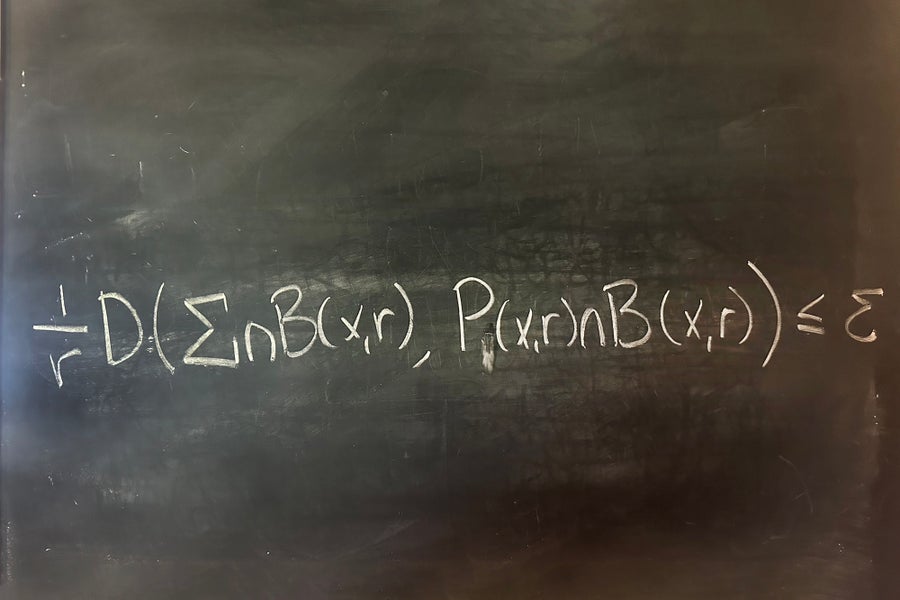
西尔维娅·吉纳西
满足图片中不等式(它们是隐藏的,但有两个!)的集合 Σ 称为赖芬贝格平坦。与往常一样,数学中的符号 ε 代表一个很小的量;我们基本上是在说,在每个球 B(x,r) 中,在每个尺度和位置,都存在一个平面 P(x,r),其与我们集合的距离非常小(εr)。
彼得·赖芬贝格在 1960 年证明,拓扑上,这些集合是圆盘。(这是一件好事:没有撕裂、孔洞或奇怪的扭曲。)事实上,正如最近的结果表明,要求这些集合稍微额外平坦会导致更平滑的参数化。对于一个集合来说,平坦性要求很高,但它在正则性方面确实得到了回报。平坦性(几何)和正则性(分析)之间的相互作用是我热爱数学一切事物的核心,这也是大多数读者已经知道但可能没有意识到的:我们很早就知道导数给了我们切线!
我不认为数学之美在于方程,尽管我确信良好的笔迹可以创造奇迹。我绝大多数时候在那些能够将两个数学宇宙结合在一起,为新概念创造空间,同时增强我们对旧概念的理解的想法中找到它。——西尔维娅·吉纳西,华盛顿大学
(1/p) + (1/q) + (1/r) = 1
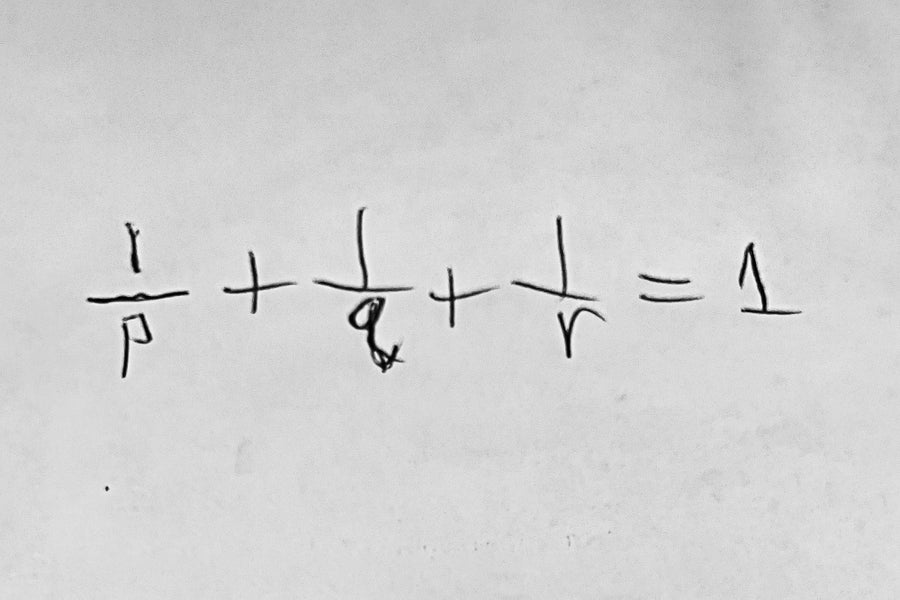
蒙蒂·麦戈文
我最喜欢的方程是 (1/p) + (1/q) + (1/r) = 1。它在正整数中唯一的解是 p = q = r = 3;p = 2, q = r = 4;和 p = 2, q = 3, r = 6。这个方程与一类称为考克斯特群或反射群的美丽群有关,并标志着这类群的有限群和无限群之间的关键边界。它的解与仅有的几种用正多边形平铺平面的方法密切相关,即用等边三角形、正方形或六边形平铺平面。——蒙蒂·麦戈文,华盛顿大学