核心概念
数学
模式
算法
谜题
简介
你是否厌倦了数学练习题和家庭作业?你知道有更多创造性的方式来锻炼你的数学能力吗?许多游戏、谜题和谜语都围绕着数学概念展开。想想简单的游戏,如井字棋,更具策略性的游戏,如国际象棋,或数学谜题,如数独。人们玩这些游戏和谜题已经有几个世纪了!它们既有趣又娱乐,有时也很有用。看看你是否喜欢这个。
背景
纵观历史,数学满足了许多实际需求,如测量土地、研究天文学和计算税收。但数学也可以用于娱乐——数学游戏、谜语、挑战和谜题也贯穿历史!
关于支持科学新闻
如果你喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,你正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
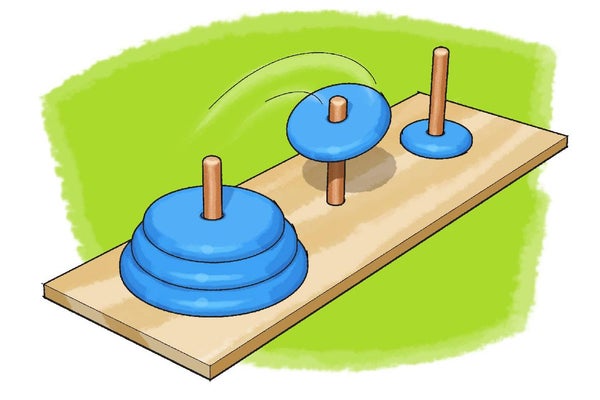
汉诺塔(也称为梵天塔或卢卡斯塔)是法国数学家爱德华·卢卡斯在 19 世纪发明的。它与一个印度寺庙的传说有关,据说该谜题被用来提高年轻祭司的心理纪律。在传说中,年轻的祭司被给予 64 个金盘,整齐地堆放在三根柱子上。每个盘子都放在一个略大的盘子上。祭司的目标是通过移动盘子,一次移动一个盘子,到另一根柱子上,重新创建堆栈,规则是较大的盘子永远不能放在较小的盘子上面。通过数学,你可以计算出,即使祭司们找到了解决问题的最有效方法,并且以每秒一个盘子的速度移动盘子,也需要近 5850 亿年才能完成这项工作。这比宇宙的年龄大 40 多倍!
你可能想知道数学是如何参与玩这个游戏的。当你用越来越多的盘子玩游戏时,你会注意到你开始寻找模式。如果你试图解释你是如何解决这个难题的,你可能会意识到你使用了以下数学概念之一
—迭代解法,其中相同的指令序列被一遍又一遍地重复
—递归解法,其中你使用一个步骤的信息来找到下一步
—模式并将这些转化为数学公式。
这些术语可能看起来难以理解。别担心!玩游戏,你可能会意识到你自己开发了这些“解决方案”。
材料
五个不同大小的盘子,如纽扣、瓶盖、容器盖等(最大的盘子的直径不能超过 5 英寸。)
纸板,大约 5 英寸 x 15 英寸
记号笔
尺子
准备
画两条直线将纸板分成三个大小相等的正方形(每个大约 5 英寸 x 5 英寸)。
步骤
从你两个最小的盘子开始游戏。将它们堆放在纸板最左边的正方形上,较小的盘子在较大的盘子之上。
游戏的起始位置是在棋盘最左边的正方形上的一个塔(就像你现在拥有的两个盘子的塔一样)。游戏的目标是在遵循以下规则的同时,将塔移动到棋盘最右边的正方形
—你一次只能移动一个盘子。
—你只能移动任何正方形最上面的盘子。
—盘子可以放置在棋盘上的空正方形上或较大的盘子上,但盘子不能并排放置在较大的盘子之上。
看看规则,你能看到不允许将盘子放在棋盘外吗?哪里说明你不能在一个正方形上开始两个塔?
尝试用你的两个盘子的塔玩游戏。你能在遵循上述规则的情况下将塔移动到最右边的正方形吗?你需要多少步?如果你感到困惑或无法完成游戏,请朋友帮助你。
重新玩两个盘子的塔的游戏。你认为你能找到“最佳”解决方案,即以尽可能少的步数完成吗?
一旦你掌握了两个盘子的塔,尝试三个盘子的塔。在最左边的正方形上堆放三个盘子(从最大到最小),然后重新开始。这次你需要多少步?
再次尝试用三个盘子的塔玩游戏。你能在更少的步数内完成游戏吗?你认为你能以尽可能少的步数完成游戏吗?
现在尝试四个盘子的塔。你能找到以尽可能少的步数完成的方法吗?你在解决三个盘子的塔时学到的任何东西能帮助你解决四个盘子的塔吗?
多玩几次游戏并仔细观察。你有没有策略?你能向朋友解释你是如何完成游戏的吗?
挑战自己,尝试五个盘子的塔。如果你有一个策略,你能将它扩展到五个盘子的塔吗?
如果你还没有策略,请不要放弃!看看你现在是否能找到一种模式。你能找到完成五个盘子的游戏所需的最少步数吗?与四个盘子的游戏相比,你需要多少步?与三个盘子的塔相比,移动四个盘子的塔需要多少步?
额外:你是否找到了一个适用于解决两个、三个、四个或五个盘子的谜题的单一策略?你能写下这个策略的步骤,以便你总是记得你是如何解决这个谜题的吗? 这个步骤列表被称为“算法”。
额外:你能在不同数量的盘子上尝试你的算法吗?它仍然有效,还是你可以调整它使其有效?
额外:如果你找到了解决两个、三个、四个或五个盘子的谜题所需的最少步数,你能看到所需的最少步数的模式吗?你能否使用该模式来预测六个盘子的游戏所需的最少步数? 也许你甚至可以找到一个方程来计算玩具有一定数量盘子的游戏所需的最少步数。(注意:该方程涉及指数。)
额外:汉诺塔游戏有很多变体。例如,你可以将正方形排列成一个圆形,并且只允许盘子顺时针移动。查找一些游戏的其他变体。新规则如何改变你能找到的解决方案?你能编写算法来解决修改后的版本吗?
观察和结果
你能在三步内移动两个盘子的堆栈吗?三步是移动这个塔所需的最少步数。也许你还在游戏中发现,三个盘子的游戏可以在七步内完成,四个盘子的游戏在 15 步内完成,五个盘子的游戏在 31 步内完成。
要以仅三步的方式玩两个盘子的游戏,将小盘子放在中间的正方形上,将较大的盘子放在最右边的正方形上,最后将较小的盘子放在较大的盘子上。玩三个盘子的游戏的一种方法是将最上面的两个盘子的堆栈移动到中间的正方形。这是两个盘子的游戏的略微变体,可以在三步内完成。然后将最大的盘子从最左边的正方形移动到最右边的正方形(一步)。接下来将现在在中间正方形的两个盘子的堆栈移动到最大的盘子之上。同样是两个盘子的游戏的略微变体,可以在三步内完成。这得出 3 + 1 + 3,即七步。类似的方法有助于玩四个盘子的游戏。首先,使用七步将最上面的三个盘子的堆栈移动到中间的正方形。然后将最大的盘子从最左边的正方形移动到最右边的正方形(一步)。现在将中间正方形的三个盘子的堆栈移动到最大的盘子之上(七步)。这得出正好 7 + 1 + 7,即 15 步。数学家称之为递归过程。要用更多盘子解决难题,你从较少数量盘子的解决方案开始。
还有其他玩游戏的方法。当以最少的步数玩游戏时,有一个模式用于开始游戏:当玩偶数个盘子时,最小的盘子移动到最右边的正方形,当玩奇数个盘子时,移动到中间的正方形。也许你还注意到你在玩游戏时会在移动最小的和下一个最小的可移动盘子之间交替。如果你仔细观察,你可能会注意到你一遍又一遍地重复同一组指令,直到塔出现在棋盘的另一侧。数学家称之为迭代解法。
更多探索 汉诺塔,来自数学论坛
为数学腾出空间,来自科学伙伴
统计科学:入口即化的数学,来自大众科学 适合所有年龄段的科学活动!,来自科学伙伴
此活动由科学伙伴合作推出