三体问题

到 2014 年春天，我基本上已经放弃了三体问题。由于没有想法，我开始在我的笔记本电脑上编程，以生成和搜索近似解。

这些尝试永远无法彻底解决我的问题，但它们可能会为答案收集证据。我缺乏编程专业知识以及由此产生的不耐烦减慢了进程，这对像我这样喜欢纸笔的数学家来说是一种不愉快的体验。我找到了我的老朋友卡尔斯·西蒙，巴塞罗那大学的一位教授，说服他帮助我进行笨拙的搜索。

那年秋天，我前往西班牙与西蒙会面，他以其在天体力学领域最有创意和最细致的数值分析师之一而闻名。他也是一个直率的人，不会浪费时间或拐弯抹角。我在他办公室的第一个下午，在我解释了我的问题之后，他用锐利的目光看着我，问道：“理查德，你为什么关心？”

关于支持科学新闻报道

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅，您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。

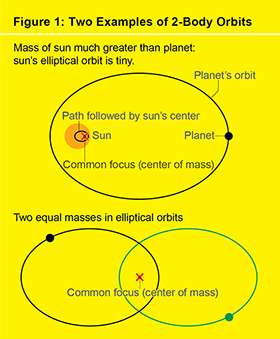
答案可以追溯到三体问题的起源。艾萨克·牛顿最初提出并解决了二体问题（见图 1），当时他在 1687 年出版了他的《原理》。他问道：“如果作用在两个质量上的唯一力是它们彼此的引力，那么这两个质量在空间中将如何运动？” 牛顿将这个问题构建为求解微分方程组的问题——这些方程根据物体当前的位置和速度来决定物体未来的运动。他完全解决了他的二体方程。这些解，也称为轨道，使每个物体都沿着圆锥曲线——圆、椭圆、抛物线或双曲线运动。在找到所有可能的轨道时，牛顿推导出了约翰内斯·开普勒的行星运动定律，开普勒在 1609 年发布的经验定律，综合了他已故雇主第谷·布拉赫数十年的天文观测。开普勒第一定律指出，每颗行星（或彗星）都沿着以太阳为焦点的圆锥曲线运动。然而，在牛顿的解中，这两个物体——太阳和行星——在两个独立的圆锥曲线上运动。这些圆锥曲线共享一个焦点，即两个物体的质心。太阳比任何行星都重得多，以至于太阳-行星系统的质心位于太阳内部，非常靠近太阳的质心，太阳的质心几乎不会在共同中心周围以微小的椭圆路径摆动。

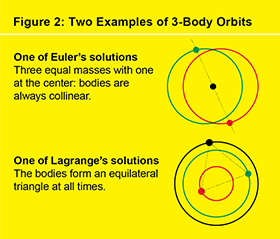
用三个质量代替两个质量，你就得到了三体问题。与其前身一样，它的轨道是微分方程组的解。然而，与其前身不同的是，找到轨道的显式公式几乎是不可能的。时至今日，尽管有现代计算机和一些最优秀的物理学家和数学家进行了数百年的工作，我们仍然只有五个轨道族的显式公式，其中三个是由莱昂哈德·欧拉（1767 年）发现的，两个是由约瑟夫-路易斯·拉格朗日（1772 年）发现的（见图 2）。1890 年，亨利·庞加莱在三体问题中发现了混沌动力学，这一发现意味着我们永远无法像牛顿对二体问题的完整解那样，在细节层面上了解该问题的所有解。然而，通过一种称为数值积分的过程，在计算机上高效完成，我们仍然可以生成近似轨道的有限段，这个过程对于空间任务的规划至关重要。通过延长计算机的运行时间，我们可以使近似值达到我们想要的精度。

日食

西蒙的话让我喘不过气来。“当然，我在乎，”我想。“我研究这个问题已经快二十年了！” 事实上，我一直专注于问题中的一个特定问题，这个问题让我很感兴趣

每个周期性日食序列是否都是平面三体问题的某个周期性解的日食序列？

让我解释一下。想象一下三个物体——把它们想象成恒星或行星——在一个平面上运动，彼此之间施加引力。将物体编号为一、二和三。有时，所有三个物体将对齐成一条直线（见图 3）。将这些时刻视为日食。（从技术上讲，这种“日食”称为合朔，是一个在绞刑游戏中无与伦比的词。）随着时间的推移，记录每次发生的日食，并将其标记为一、二或三，以表示哪颗恒星在中间。通过这种方式，我们得到一个由一、二和三组成的列表，称为日食序列。

例如，在我们简化的太阳-地球-月球系统中，月球（我们将其标记为物体“3”）每月绕地球（物体“2”）转一圈，而地球每年绕太阳（物体“1”）转一圈。这种运动是重复的，所以它会给我们一个周期性的日食序列。具体来说：2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3、2、3。序列中没有 1，因为太阳永远不会落在地球和月球之间。一年中，该列表长 24 个数字，一年 12 个月，每个月都有一个 2、3。

解决方案的日食序列没有理由必须重复自身。它可能会永远持续下去，没有明显的模式。但是，如果解决方案在一段时间后完全重复自身，就像地球-月球-太阳系统在一年后一样，那么序列会重复：地球-月球-太阳系统的相同 24 个数字每年都会重播。所以，回到我的问题：每个周期性日食序列是否都是平面三体问题的某个周期性解的日食序列？我怀疑答案是肯定的，但我无法证明。

带孔物体

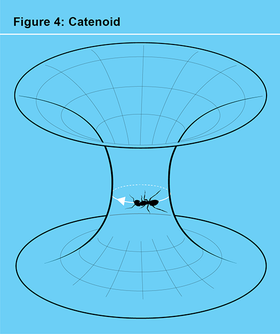
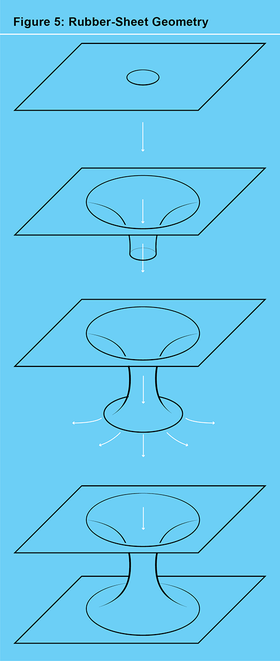
为了证明我的问题的重要性，我提醒西蒙一个基本事实，它将数学的三个分支联系在一起：拓扑学，有时称为橡皮膜几何；黎曼几何，弯曲曲面的研究；以及动力学，事物运动方式的研究。想象一只虫子沿着一个弯曲的表面行走，这个表面形状像“虫洞表面”，也称为悬链面（见图 4）。虫子的工作是找到绕孔一周的最短回路。就拓扑学而言，虫洞表面（见图 5）与x-y平面上穿了一个孔的表面相同。实际上，想象一下一个孔穿过一块柔性橡皮膜。通过向下推孔并向外拉伸它，你可以制作出虫洞表面。如果孔已经充分向外张开，那么不仅存在这个最短回路，而且它还满足一个非常类似于三体方程的微分方程。通过这种方式，我们的虫子找到了一个有趣的微分方程的周期解。

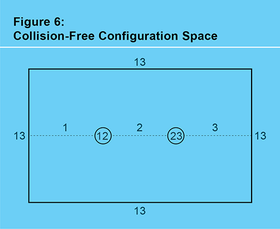
在三体问题中，虫洞表面的作用由称为配置空间的东西来扮演——一个空间，其点同时编码所有三个物体的位置，因此配置空间中的一条曲线指定了三个物体中每个物体的运动。通过坚持我们的物体不相互碰撞，我们在配置空间中穿孔。正如我们将看到的，就拓扑学或橡皮膜几何而言，由此产生的无碰撞配置空间与x-y平面上穿了两个孔的平面相同（见图 6）。我们将孔标记为“12”，表示物体 1 和 2 发生了碰撞，将孔标记为“23”，表示物体 2 和 3 发生了碰撞，并将孔放在x轴上。我们还将在无穷远处放置第三个孔，并将其标记为“13”，以表示物体 1 和 3 碰撞。这些孔将x轴分成三个段，分别标记为 1、2 和 3。这个两次穿孔平面中的一条曲线表示所有三个物体的运动——也就是说，三体问题的潜在解。当曲线穿过段 1 时，表示发生了 1 型日食，同样，穿过段 2 或 3 时也是如此。通过这种方式，日食序列表示围绕我们的碰撞孔缠绕的方式。

现在，我们的虫子试图最小化其路径的长度，因为它绕着虫洞绕了一圈。为了获得虫子问题和三体问题之间的正确类比，我们必须用一个称为路径作用量的量代替路径的长度。（作用量是路径表示的运动的瞬时动能减去势能的平均值。）力学中一个古老的定理指出，配置空间中任何最小化作用量的曲线都必须是牛顿三体问题的解。因此，我们可以尝试通过在产生固定日食序列的所有闭合路径中搜索那些最小化作用量的闭合路径来解决我们的日食序列问题。

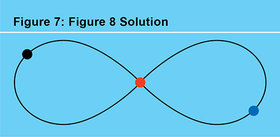
这种策略——在配置空间中为具有特定日食序列的环路寻求最小化作用量——在过去 17 年的大部分时间里一直困扰着我，并导致了许多不错的结果。例如，在 2000 年，巴黎狄德罗大学的阿兰·切辛纳和我重新发现了似乎是零角动量三体问题的第一个已知周期解。这是一个 8 字形解（见图 7），最早由圣塔菲研究所的克里斯·摩尔在 1993 年发现。在这种情况下，三个质量相等的物体在平面上沿着 8 字形相互追逐。它的日食序列是 123123，永远重复。我们的工作普及了 8 字形，并给出了严格的存在性证明。它还导致了对等质量N体问题的许多新轨道的爆炸式发现，这些轨道被西蒙（见图 8）命名为“舞蹈”，他发现了数百个这些新的轨道族。我们的 8 字形轨道甚至进入了刘慈欣的畅销中国科幻小说，其英文译名为《三体问题》。

在我与西蒙分享我的思考的第二天早上，他说了一些深深影响我的话。“理查德，如果你对你的问题的想法是真的，那么一定存在一种动力学机制。” 换句话说，如果我对我问题的答案是肯定的看法是正确的，那么一定存在一些关于这些物体如何运动的因素使之如此。

这几个字让我质疑我的信念，并让我放弃了长达 17 年的尝试，即通过最小化路径的作用量来回答我的问题。我对这个问题中的哪些动力学机制有所了解？我想知道。我能想到两种，其中只有一种抱有希望。这种机制与庞加莱发现的混沌有关，它让我反思了我最近的一位合作者，明尼苏达大学的里克·莫克尔的旧作。在 20 世纪 80 年代，他展示了来自三体问题中的三重碰撞的称为双曲缠结的曲线如何导致惊人的结果。当我重读他的旧论文时，我觉得莫克尔掌握了我问题的关键。我联系了他，几天之内，莫克尔和我回答了我的问题！好吧，几乎。我们回答了一个无限接近的问题。

形状球体

理解莫克尔的动力学机制，以及三体配置空间与上面描述的带有两个孔的平面之间的关系，需要思考一个称为形状球体的物体。当三个物体在平面上移动时，它们在每个瞬间都形成三角形的三个顶点。与其跟踪每个顶点的位置，不如只跟踪三角形的整体形状。结果是形状球体上的曲线，形状球体是一个球体，其点表示三角形的“形状”。

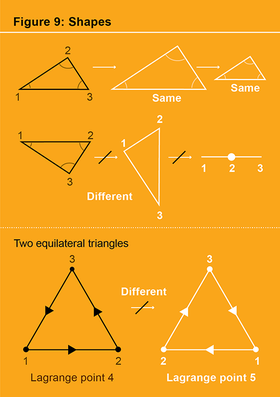
什么是“形状”？如果我们可以通过平移、旋转或缩放一个图形将其变成另一个图形，则平面中的两个图形具有相同的形状（见图 9）。从通常的三体配置空间（也就是说，从了解三角形所有三个顶点的位置）传递到形状球体中的点的操作是一个遗忘的过程——忘记三角形的大小、其质心的位置以及三角形在平面中的方向。形状球体是二维的，这很容易从高中几何学中理解：如果我们知道三角形的所有三个角，我们就知道三角形的形状，但由于三个角的总和始终为 180 度，我们实际上只需要三个角中的两个角——因此，两个数字足以描述三角形的形状。形状球体实际上是一个球体，这更难理解，并且要求我们允许三角形退化，也就是说，我们允许由位于同一条线上的三个顶点组成的“三角形”被称为三角形。这些所谓的退化零面积三角形构成了形状球体的赤道：它们就是日食！

三角形的面积除以其大小 (r) 的平方，是其到赤道的距离。球体的北极和南极代表那些具有最大可能面积的三角形，并且是两个等边三角形形状。但是为什么有两个等边形状呢？这两个等边三角形形状因其顶点的循环顺序而不同（见图 9）。无法通过平面的旋转、平移或缩放将其中一个等边三角形变成另一个等边三角形：它们代表不同的形状。然而，在平面中绕一条线（任何线）反射的操作会将一个等边三角形形状变成另一个等边三角形形状。这种反射操作作用于所有三角形，因此也作用于形状球体本身，在形状球体中，它通过绕赤道反射来起作用，保持赤道（退化三角形）的点固定，同时交换南北半球。

在退化三角形中，包括二元碰撞：那些“三角形”，其中三个顶点中的两个顶点彼此重叠。恰好有三个这样的二元碰撞三角形，标记为“12”、“23”和“13”，具体取决于哪两个顶点彼此重叠。

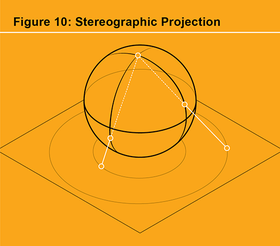
我现在可以解释形状球体如何向我们展示三体配置空间在拓扑上与通常的x-y平面减去两个点相同。我们必须知道，球体减去一个点在拓扑上与通常的x-y平面是相同的对象（见图 10）。了解关于球体的这个事实的一种方法是使用球面投影，它将移除了单个点（“光源”）的球体映射到通常的x-y平面上。当球体上的一个点趋向于光源时，它在x-y平面上的图像点会移动到无穷远，因此我们也可以说，添加了无穷远点的平面在拓扑上等于球体。将光源视为形状球体的 13 二元碰撞点，以便x-y平面的无穷远点对应于 13 碰撞点。定向球体，使其赤道面与x-y平面的x轴相交。然后球面投影将退化三角形的赤道映射到平面的x轴，而其他两个二元碰撞点被映射到该x轴上的两个点。通过这种方式，我们恰好得到了前面描述的图片。

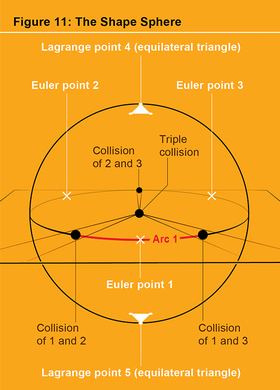
三个二元碰撞点在形状球体上形成三个特殊点。除了这三个点之外，形状球体上还有其他特殊点，称为中心构型。这五个中心构型对应于欧拉和拉格朗日发现的五个解族。它们的解是唯一的三体解，其中三角形的形状在三角形演化过程中不会改变！在拉格朗日解中，三角形在每个瞬间都保持等边形；正如我们所见，存在两种拉格朗日构型，它们构成了形状球体的北极和南极（见图 11）。我们将它们标记为“拉格朗日点 4”和“拉格朗日点 5”。其余三个中心构型是欧拉构型，标记为“欧拉点 1”、“欧拉点 2”和“欧拉点 3”。它们是共线的（都在一条线上），退化的构型，因此它们位于
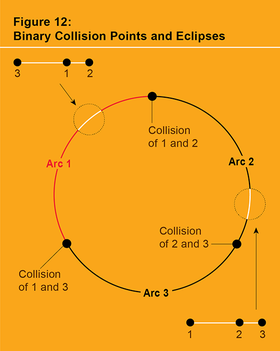
形状球体的赤道。它们位于赤道上，介于三个二元碰撞点之间（见图 12）。（它们沿赤道的间距取决于物体三个质量之间的质量比。）例如，欧拉点 1 位于标记为 1 的赤道弧上，因此是物体 1 位于物体 2 和 3 之间的共线形状。（通常，所有五个中心构型点都称为拉格朗日点，其中欧拉点标记为“L1”、“L2”和“L3”。）

人们可以通过掉落三个物体来理解中心构型解，我的意思是，让三个物体从静止开始，没有初始速度。通常，当人们这样做时，会发生各种疯狂的事情：近距离二元碰撞、狂野的舞蹈，甚至可能是一个物体逃逸到无穷远。但是，如果在一个物体以五个中心构型形状之一排列时掉落这三个物体，那么它们形成的三角形只会缩小到一个点，保持与开始时完全相同的形状，三个质量均匀地相互拉动，直到解以同时三重碰撞结束。

通往三重碰撞的五条道路

三重碰撞是三体问题中的一个本质奇点，有点像问题中心的大爆炸，它是其大部分混沌和困难的根源。在 20 世纪初，芬兰数学家卡尔·桑德曼证明，五个中心构型（如刚刚描述的掉落解所代表的那样）是通往三重碰撞的唯一道路。这意味着任何以三重碰撞结束的解都必须以非常接近这五个掉落的中心构型解之一的方式接近它，并且随着它越来越接近三重碰撞，解的形状必须接近五个中心构型形状之一。

桑德曼的工作是一项复杂的代数和分析壮举。然后，在我高中毕业的那一年（完全没有注意到三体问题），美国数学家理查德·麦戈希发明了他的所谓膨胀方法，该方法使我们能够以图形方式理解桑德曼的工作，并更详细地研究三重碰撞附近的动力学。设 r 表示到三重碰撞的距离——三角形整体大小的度量。随着 r 接近于零，牛顿方程变得非常糟糕，许多项趋于无穷大。麦戈希找到了配置空间变量和时间的变化，这减慢了接近三重碰撞的速度，并将三重碰撞点（即 r = 0）变成了一整组点：碰撞流形。惊喜！碰撞流形本质上是形状球体。麦戈希的方法扩展了牛顿方程，最初牛顿方程仅对大于零的 r 有效，扩展为一个微分方程组，当 r = 0 时也有意义。

牛顿方程没有平衡点，这意味着没有三个物体的构型可以静止不动：三颗恒星，彼此吸引，不能只是静止在空间中而不移动。但是，当牛顿方程扩展到碰撞流形时，平衡点就出现了。恰好有 10 个平衡点，每个平衡点对形状球体上的五个中心构型点中的每个点都有一对。一对中的一个元素表示相应掉落的中心构型在其接近三重碰撞时的最终结果。牛顿方程即使我们倒退时间也保持不变，因此我们可以反向运行任何解并获得另一个解。当我们反向运行掉落的中心构型解时，我们会得到一个从三重碰撞中爆炸出来的解，在掉落的构型处达到其最大尺寸。该对的另一个元素表示此“爆炸”解的初始起点。这两个中心构型解——碰撞和喷射——平滑地拟合在一起，形成一个单一的喷射-碰撞解，该解离开 r = 0 处的喷射平衡点，进入 r 大于零的区域，在该区域中，它达到最大尺寸，然后缩小以在三重碰撞流形上结束于那里的碰撞平衡点。这个完整的解将平衡对的一个元素连接到另一个元素。

通过创建与中心构型相关的这些平衡点，这些平衡点深深地埋藏在三体问题中，麦戈希给了莫克尔一个密钥，使他能够应用现代动力学系统中的最新成果——牛顿、拉格朗日或桑德曼无法获得的成果——从而在三体问题上取得一些有趣的进展。

莫克尔的游走

在莫克尔的论文中，我看到了一张图，其中有五个顶点，标记为中心构型，并通过边连接在一起（见图 13）。

图上的游走是穿过其顶点的可能回路，沿着边从一个顶点行进到另一个顶点。莫克尔证明，你可以在他的图上进行的任何可能的游走都对应于三体问题的解，该解在一段时间内接近于由相应顶点标记的中心构型解。例如，游走 E1 L4 E2 L5 对应于一个非常接近与欧拉点 1 相关的欧拉喷射-碰撞解的解，然后接近几乎沿着拉格朗日 L4 中心构型解的三重碰撞，但在实现完全三重碰撞之前，这三个物体沿着五条“道路”之一射出，非常接近欧拉点 2 中心构型解。然后，最终，当这个欧拉解向三重碰撞坍缩时，该解会旋出成拉格朗日 L5 等边形状。此外，如果我们重复相同的游走，使其周期性，则跟随它的解也将是周期性的。

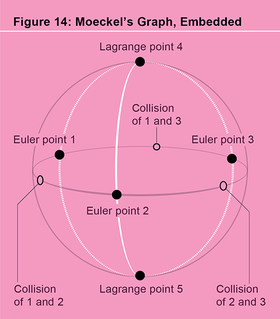
在西蒙告诉我必须存在动力学机制后不久，我意识到莫克尔的图嵌入到形状球体中（见图 14）。关于这个嵌入图的重要之处在于，它承载了带有三个二元碰撞孔的球体的所有拓扑结构。实际上，我们可以将三次穿孔球体变形到图上，并在这样做时将穿孔球体中的任何环路变成图上的游走。为了看到这种变形，将球体想象成气球的表面。在气球上戳三个针孔，每个针孔位于一个二元碰撞孔处。气球由非常柔韧的材料制成，因此我们可以拉伸我们的三个针孔，扩大它们，直到三个孔的边缘几乎相互接触，并且剩余的材料形成一条紧贴嵌入图的带状物。在进行这种变形的过程中，三次穿孔球体中的任何闭合环路都会变形为这个带状结构中的闭合环路，并从那里变形为莫克尔的嵌入图上的游走。

为了将这张图变成关于解的定理，我需要证明，如果我将莫克尔定理保证的解投影到形状球体上，那么它们永远不会偏离这个嵌入图太远。如果它们偏离得太远，它们可能会缠绕在二元碰撞周围，甚至会撞击其中一个，从而杀死或添加一些拓扑上重要的环路，从而改变日食序列。我给莫克尔发电子邮件寻求帮助。他回复道：“你的意思是你要强迫我读我 20 多年前写的论文？” 尽管如此，他还是重新投入到他的旧研究中，并证明他多年前以符号方式编码的解的投影永远不会偏离嵌入图太远。我的问题得到了解答——几乎。

为了使他的证明奏效，莫克尔需要一点点角动量。（在这种情况下，角动量是衡量系统总“旋转”量的指标，并且对于每个解都是恒定的。）但在我与西蒙对话之前的 17 年里，我一直坚持要求解具有零角动量。这种坚持源于在具有给定日食序列的所有曲线中最小化作用量的解必须具有零角动量。另一方面，莫克尔需要少量角动量才能使解沿着他的图的边行进。数学分析中微小正量的符号是 epsilon。我们需要 epsilon 的角动量。

莫克尔的结果还有另一个问题：当他的解在欧拉点 E1、E2 和 E3 附近穿过形状球体的赤道时，它们将在那里在赤道上来回振荡，然后再向上移动到北极或南极，因为它们沿着相应的拉格朗日道路 L4 或 L5 接近三重碰撞。为了解释这些振荡，取一个正整数 N，如果序列中每次出现一个数字，则称日食序列为“N 长”，它至少连续出现 N 次。例如，序列 1112222333332222 是 3 长的，但它不是 4 长的，因为只有三个 1 连续出现。

最后，这是我们的主要定理：考虑具有小非零角动量 epsilon 和大开放范围内的质量的三体问题。那么存在一个大的正整数 N，它具有以下意义。如果我们选择任何日食序列——它是 N 长的——那么就存在一个相应的我们三体问题的解，该解恰好具有这个日食序列。如果该序列被设置为周期性的，那么实现它的解也是周期性的。

我最初的问题呢？那里没有提到大的 N。我问的是每个日食序列。但我没有告诉你我的真正问题。我真正想知道的是我是否可以实现周期曲线的任何“拓扑类型”，而不是任何日食序列。我使用日食序列作为一种方便的简写或编码拓扑类型的方式，也就是说，作为一种编码环路绕三个二元碰撞孔的缠绕模式的方式。闭合曲线的拓扑类型的日食序列表示具有冗余：许多不同的日食序列编码相同拓扑类型的曲线。例如，考虑拓扑类型“绕过排除二元碰撞 23 而形成的孔一次”。
日食序列 23 表示这种拓扑类型。日食序列 2223、222223 和 2333 也是如此。每当我们连续两次穿过弧 2 时，我们可以通过拉直曲折来取消它们，使曲线在那部分保持在一个半球或另一个半球中，而不会穿过赤道（见图 15）。实际上，我们可以取消在日食序列中出现的任何连续的相同数字对，而不会改变序列表示的闭合曲线的拓扑类型。

为了使用我们的主要定理来回答我的真正问题，请注意，通过删除连续对，我可以确保编码给定拓扑类型的日食序列永远不会有两个连续的相同类型的数字：没有“11”或“22”或“33”。将这样的序列称为可容许序列。现在，取任何可容许序列，例如 123232。请允许我在写下日食序列时使用指数表示法，因此，例如，1³ = 111。选择一个奇数整数 n，它至少与我们的主要定理的数字 N 一样大。将可容许序列替换为更长的序列 1ⁿ 2ⁿ 3ⁿ 2ⁿ 3ⁿ 2ⁿ 并使其周期性延续。这个更长的序列表示相同的原始选择的拓扑类型，因为 n 是奇数。我们的定理表明，这个更长的序列由周期解实现。这个周期解表示我们原始的拓扑类型 123232。

下一步是什么？

我们还有很多工作要做。当我大约 20 年前最初提出我的问题时，我只想要具有零角动量的解。但是越来越多的证据表明，在零角动量的情况下，我对我的问题的答案是“否”。我们有一些证据表明，即使是最简单的非空周期序列 23 也永远无法通过等质量、零角动量三体问题的周期解来实现。

我们在这里提出的主要问题，即使对于角动量 epsilon，仍然是开放的，因为我们的定理只允许我们实现对于某个大的 N 来说是 N 长的序列。例如，我们不知道如何实现可容许序列，即可容许序列是没有相同类型的连续数字的序列。

最终，我们可能并没有更接近传统意义上的“解决”三体问题，但我们学到了很多。我们将继续努力——对于我们这些被它吸引的人来说，这个问题将继续结出硕果。事实证明，从数学史上最经典的难题之一中仍然可以获得新的见解。