想想午餐。也许是一份美味的火腿三明治。一把刀应该能干净利落地将火腿和两片面包一分为二。但如果你失手了呢?糟糕——火腿现在折叠在翻转的盘子下面;一片面包掉在地板上,另一片粘在了天花板上。这里有一些安慰:几何学保证,只需一刀直线切割,也许用一把房间大小的弯刀,仍然可以完美地将你掉落的午餐分成两半,使火腿和每片面包都恰好一半在切割线的两侧。这是因为数学的“火腿三明治定理”保证,对于任意三个(可能不对称的)物体,在任何方向上,总会有一条直线切割可以同时将它们全部一分为二。这个事实有一些奇怪的含义,以及一些令人警醒的含义,因为它与政治中的选区划分不公有关。
该定理可以推广到其他维度。更数学化的措辞是,n 维空间中的 n 个物体可以被 (n – 1) 维切割同时平分。火腿三明治有点难以下咽,但我们会让它更容易理解。在二维纸上,你可以画出任何你想要的两个形状,并且总会有一条(一维)直线将两者完美地切成两半。为了保证对三个物体进行均等切割,我们需要升级到三维空间,并用二维平面进行切割:将那把破坏房间的弯刀想象成一张薄纸,你将其滑入房间的两半之间。在三维空间中,弯刀有三个自由度:你可以前后移动它穿过房间,停下来并将其旋转到不同的角度,然后左右摇晃弯刀(就像你可能倾斜刀子以斜切胡萝卜而不是直线切割一样)。
如果你能想象一个四维火腿三明治,就像数学家喜欢做的那样,那么你可以想象如何用三维切割来平分第四种成分。
支持科学新闻事业
如果您喜欢这篇文章,请考虑支持我们屡获殊荣的新闻报道,方式是 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
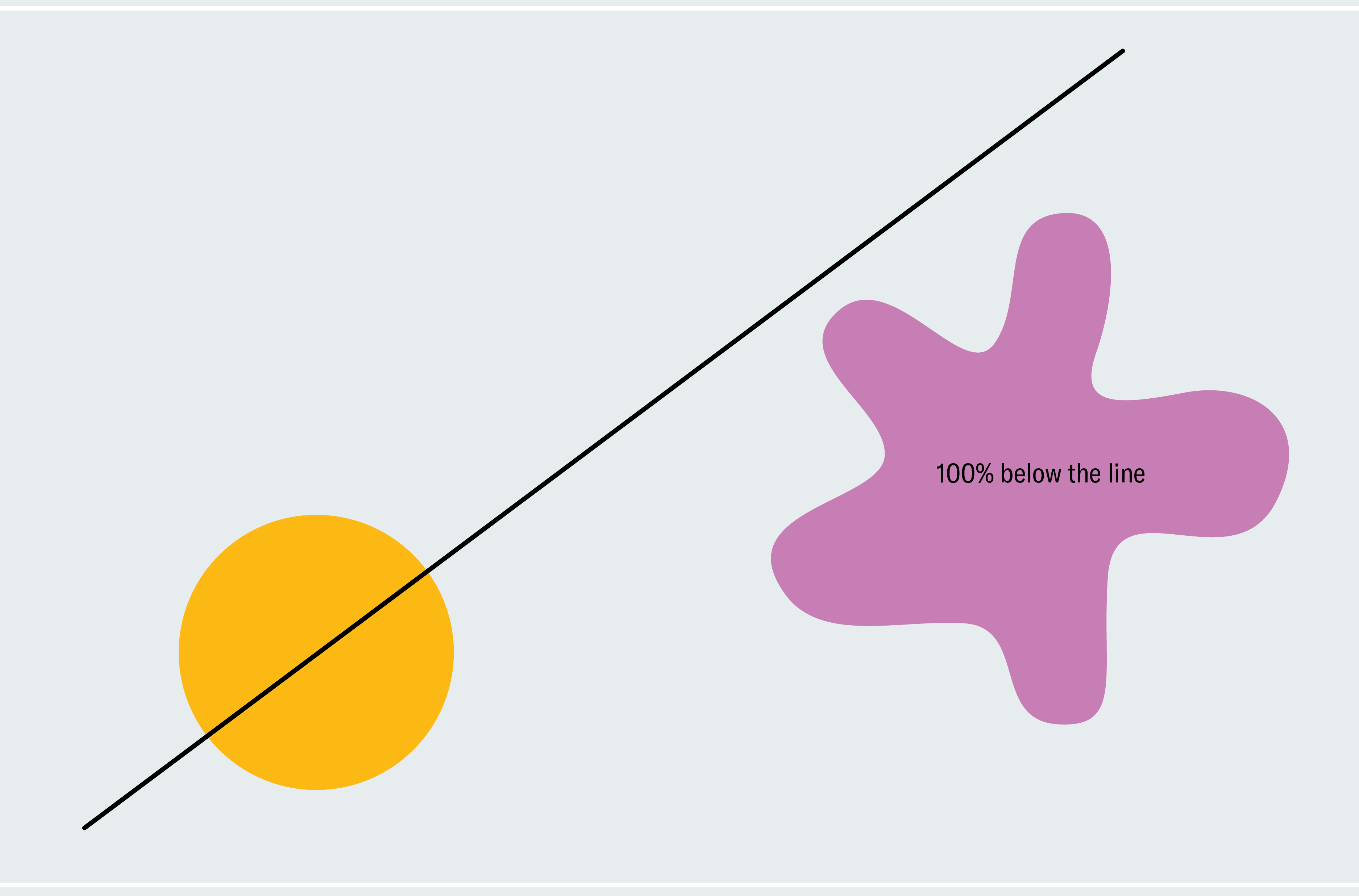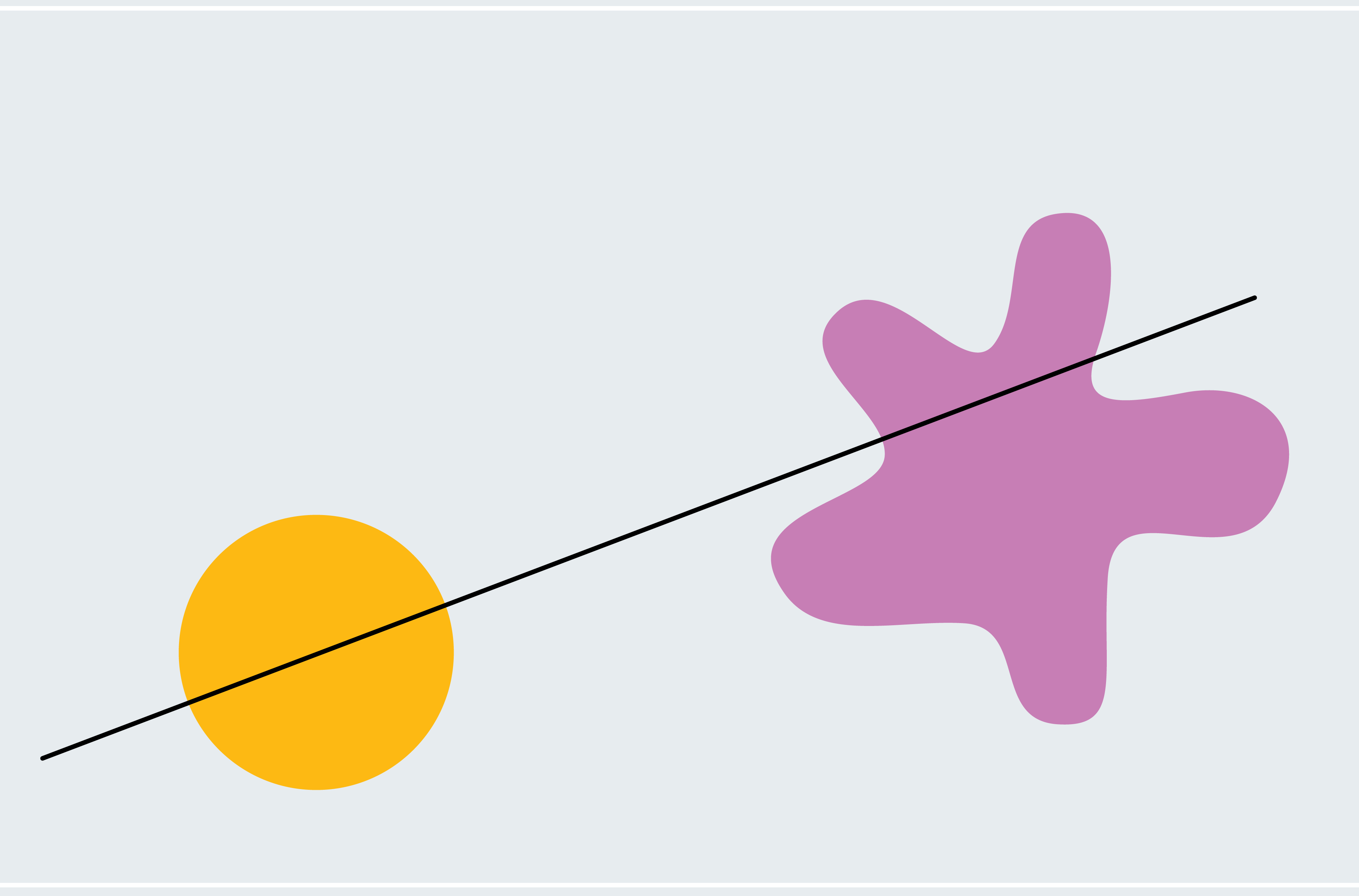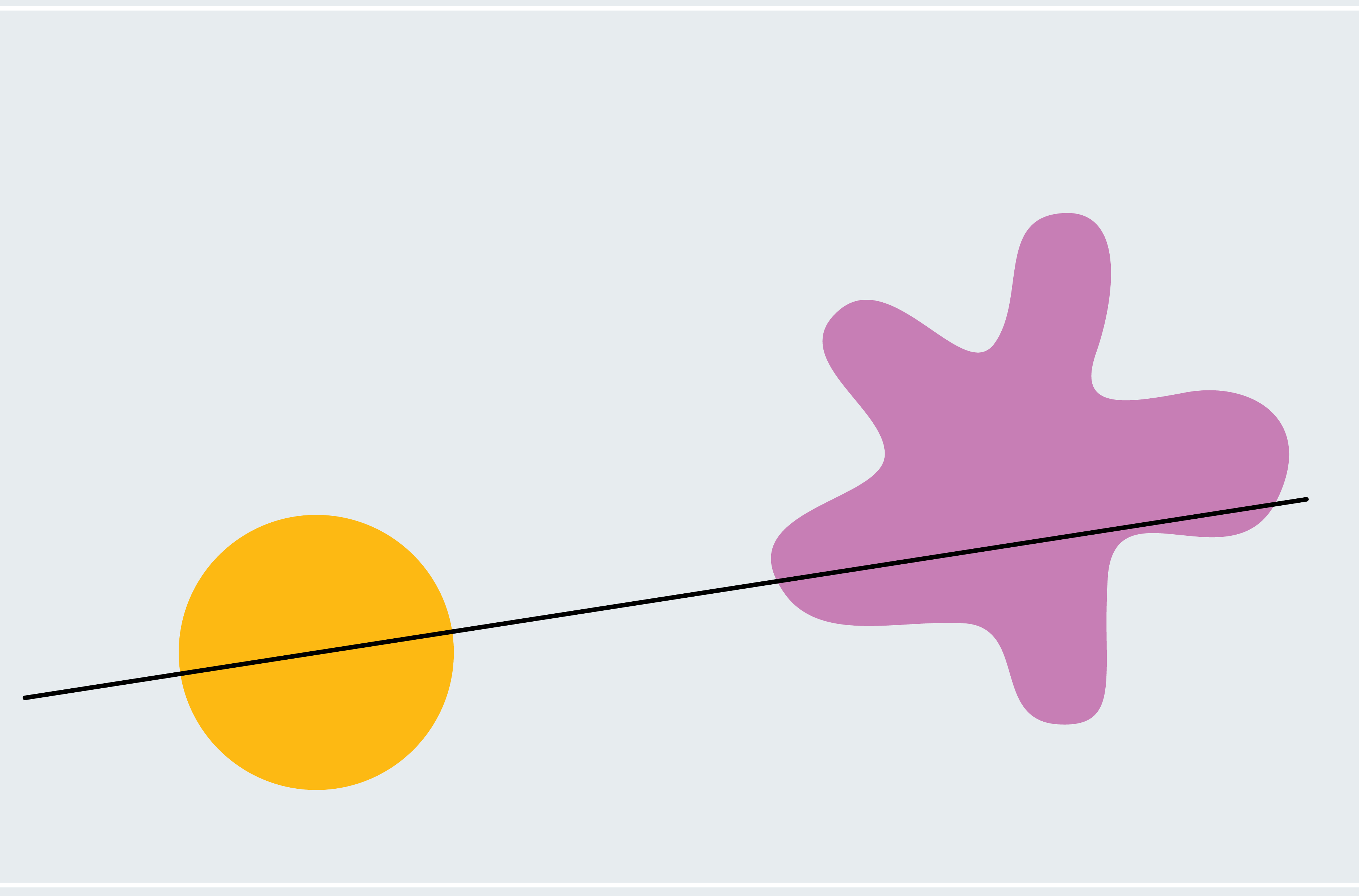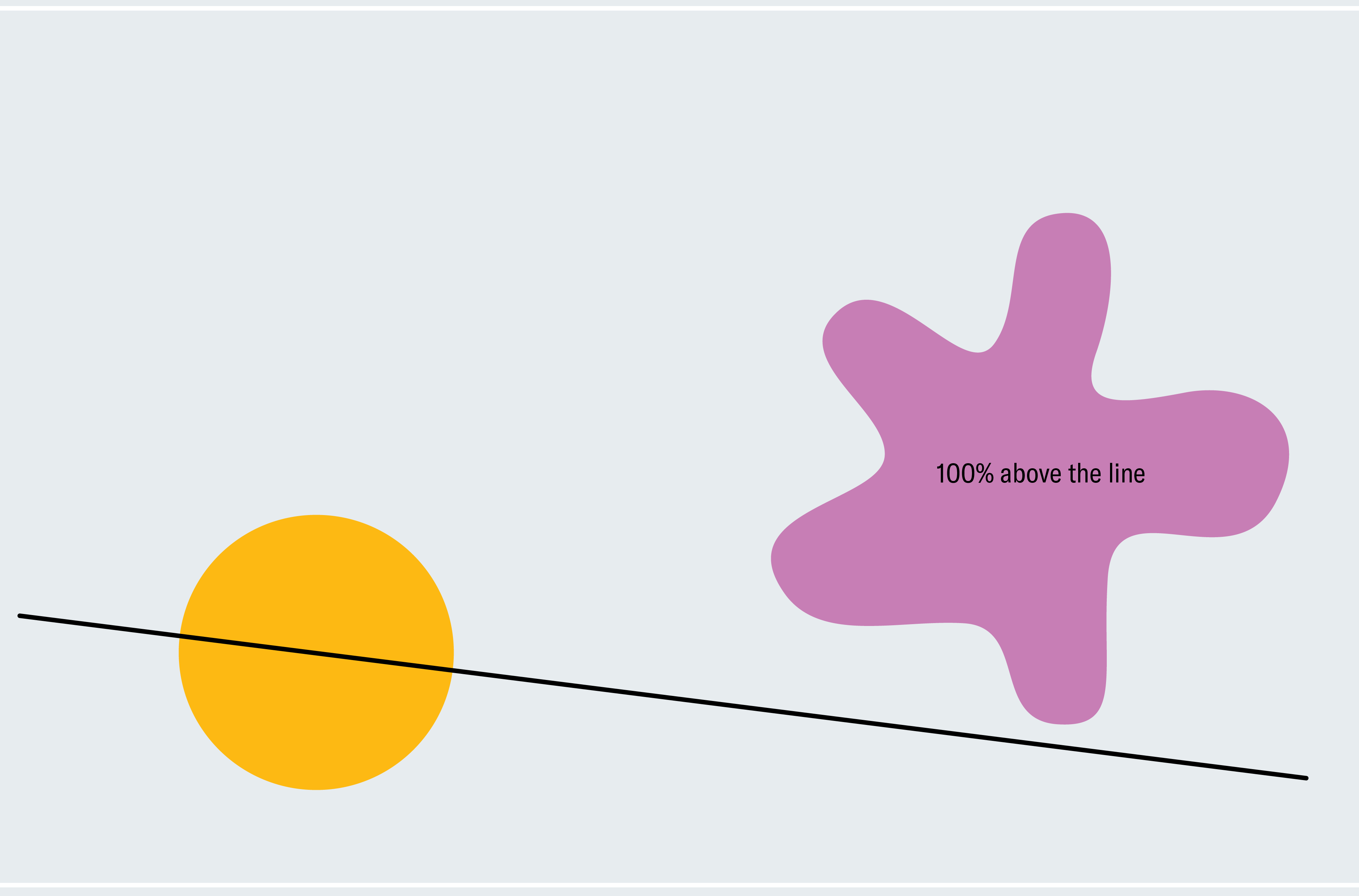
为了了解如何证明火腿三明治定理,请考虑一个简化的版本:两个二维形状,一个圆形,另一个斑点状。任何穿过圆心的线都会平分圆(不对称形状不一定有真正的中心;我们现在使用圆形是为了让事情更简单)。我们如何知道某条线也平分斑点状形状?选择一条穿过圆心但不与斑点状形状相交的线。如下一栏图形的第一幅图所示,斑点状形状的 100% 位于我们的线下方。现在像风车轮一样围绕圆心缓慢旋转这条线。最终,它会突破斑点状形状,切割越来越多的部分,然后穿过它下方,使斑点状形状的 0% 位于线下方。从这个过程中,我们可以推断出一定存在一个时刻,斑点状形状的 50% 位于线下方。我们正在逐渐但连续地从 100% 移动到 0%,因此我们必须经过介于两者之间的每个量,这意味着在某个时刻我们恰好达到 50%(微积分爱好者可能会将此识别为介值定理)。
这个论证证明存在一条线可以同时平分我们的形状(尽管它没有告诉我们这条线在哪里)。它依赖于一个方便的事实,即每条穿过圆心的线都会平分圆,因此我们可以自由旋转我们的线,并专注于斑点状形状,而无需担心忽略圆。两个不对称形状需要我们风车技术的更微妙的版本,而扩展到三维空间则需要更复杂的论证。
有趣的是,即使火腿和面包被切成多块,该定理也适用于我们的三明治。使用饼干切割器冲压出火腿雪人,然后将面包切成方块并烤成面包丁;一个完全均等的切割将始终存在(单个雪人和面包丁不一定会被平分,但火腿和面包的总量将会被平分)。
阿曼达·蒙塔涅斯
将这个想法推向极致,我们可以对点做出类似的断言。在一张纸上画出散落的红色和绿色点,并且总会有一条直线,其两侧分别有恰好一半的红点和一半的绿点。这个版本需要一个小小的技术细节:恰好位于分割线上的点可以算在任一侧,也可以完全不算(例如,如果你有奇数个红点,那么如果没有这个注意事项,你永远无法均匀地分割它们)。
思考一下这里奇怪的含义。你可以画一条横跨美国的线,使恰好一半的国家的臭鼬和一半的 Twix 巧克力棒位于这条线的上方。虽然臭鼬和 Twix 巧克力棒实际上不是单个点,但与广阔的美国陆地相比,它们也可以被视为点。将维度提升一级,你可以在地球上画一个圆圈(切穿地球仪会留下圆形横截面),其中包含世界上一半的石头、一半的纸和一半的剪刀,或者任何其他你希望的古怪类别。
对于长期存在的选区划分不公问题,火腿三明治定理的后果远没有那么异想天开。在美国,州政府将其州划分为选区,每个选区选举一名美国众议院议员。选区划分不公是指为了政治利益而刻意划分这些选区边界的做法。
作为一个简化的例子,想象一个拥有 80 人的州;其中 75% 的人(60 人)支持紫色党,25% 的人(20 人)喜欢黄色党。该州将被划分为四个选区,每个选区 20 人。似乎很公平的是,其中三个选区(75%)应该是紫色,第四个应该是黄色,以便该州在国会的代表性与人口的偏好相符。然而,一位狡猾的地图绘制者可以扭曲选区边界,使每个选区包含 15 名倾向于紫色的选民和 5 名投票给黄色党的人。这样,每个选区都将是紫色多数,并且该州 100% 的代表权将来自紫色党,而不是 75%。事实上,如果有足够的选民,一个政党对另一个政党的任何百分比优势(例如,紫色对黄色 50.01% 对 49.99%)都可以被利用来帮助该政党赢得每个选区;只需使每个选区 50.01% 的人支持它即可。

阿曼达·蒙塔涅斯
当然,这些选区看起来非常人为。遏制选区划分不公的一个看似显而易见的方法是限制选区的形状,并禁止我们在美国选举地图上经常看到的触手状怪物。事实上,许多州都施加了此类规则。虽然强制执行“正常”选区形状似乎可以在很大程度上缓解问题,但聪明的研究人员已经应用了某个几何定理来表明这纯粹是胡说八道。
让我们回顾一下我们的例子:总共有 80 名选民,其中 60 名紫色党支持者和 20 名黄色党支持者。火腿三明治定理告诉我们,无论他们如何分布,我们都可以画一条直线,两侧分别有恰好一半的紫色选民和一半的黄色选民(两侧各有 30 名紫色选民和 10 名黄色选民)。现在将你创建的两个区域视为新的火腿三明治,用各自的直线将每个区域分成两半,以便每个生成的区域包含 15 名紫色选民和 5 名黄色选民。紫色党现在拥有与之前相同的选区划分不公优势(它赢得了每个选区),但生成的区域都是具有直线边界的简单形状!
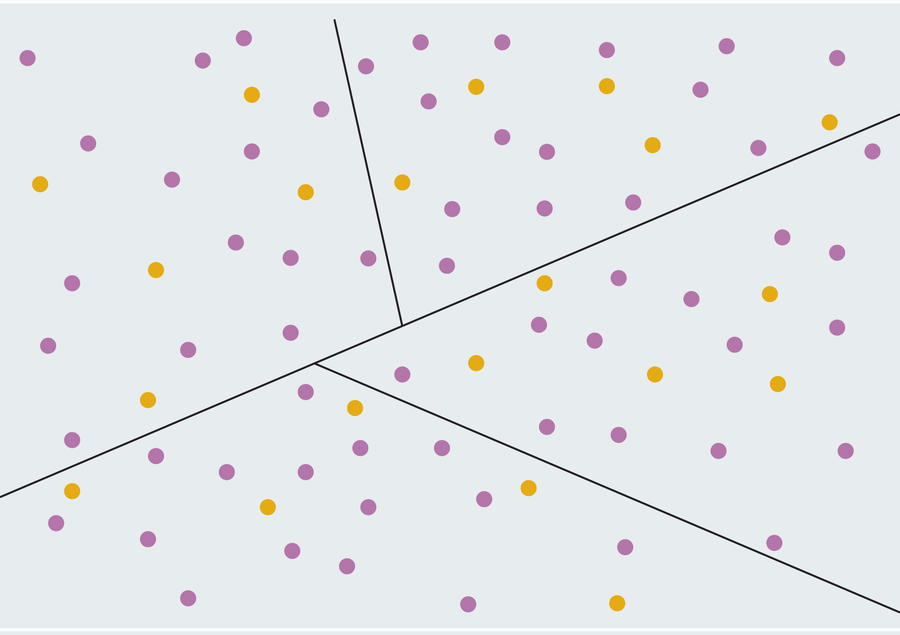
阿曼达·蒙塔涅斯
重复的火腿三明治细分将始终产生相对简单的选区(在数学术语中,它们是凸多边形,除非它们可能与现有州边界共享边界)。这意味着对国会选区形状的基本规定可能无法排除最糟糕的选区划分不公情况。虽然数学和政治可能看起来是遥远的领域,但一个闲置的几何学消遣告诉我们,针对选区划分不公的最自然的解决方案并不能解决问题。
