让我们创建一个与众不同的真人约会节目,关键在于一个方面。首先,我们将在热带岛屿上租一栋别墅。然后,我们将空运五名男性和五名女性,他们每个人都有自己的(异性恋)约会偏好。然而,我们的目标与爱之岛系列节目截然相反:我们绝对不想要任何戏剧性场面。我们能否确保每个人都与伴侣配对并坚持下去,而不会产生嫉妒?
数学家们将这个困境称为“稳定匹配问题”或“稳定婚姻问题”。尽管情场之事可能变幻莫测,但研究人员已经证明,通过使用一个简单的算法,他们总是可以找到两组人数相等的成员之间稳定的匹配集合。已故数学家劳埃德·沙普利因发现该算法而分享了2012年诺贝尔经济学纪念奖——这是有充分理由的:它至今仍用于将住院医师与医院、儿童与学校配对,甚至启发了约会应用程序算法。
根据数学家的说法,当两个人都没有更好的选择时,关系才是稳定的——至少,没有也对他们感兴趣的选择。那么,不稳定可能看起来像这样:想象一下爱丽丝目前与鲍勃配对,而查理目前与达琳配对。然而,鲍勃暗恋达琳,而达琳无法忍受再与查理相处一天。因为鲍勃和达琳似乎准备私奔并抛弃他们的伴侣,所以数学家称这种情况为不稳定。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
同样的困境也出现在浪漫生活之外。沙普利和数学家大卫·盖尔最初将其描述为大学招生的问题:什么样的申请流程可以确保大学和申请者(每个都有自己的一套偏好)对他们的选择感到满意?1962年,盖尔和沙普利表明,对于任何一组学生和大学(或约会节目示例中的男性和女性),总是存在一组配对,其中每个匹配都是稳定的。更重要的是,他们提供了一个简单的过程或算法,该算法会收集每个人的排名并建立相对幸福的配对。
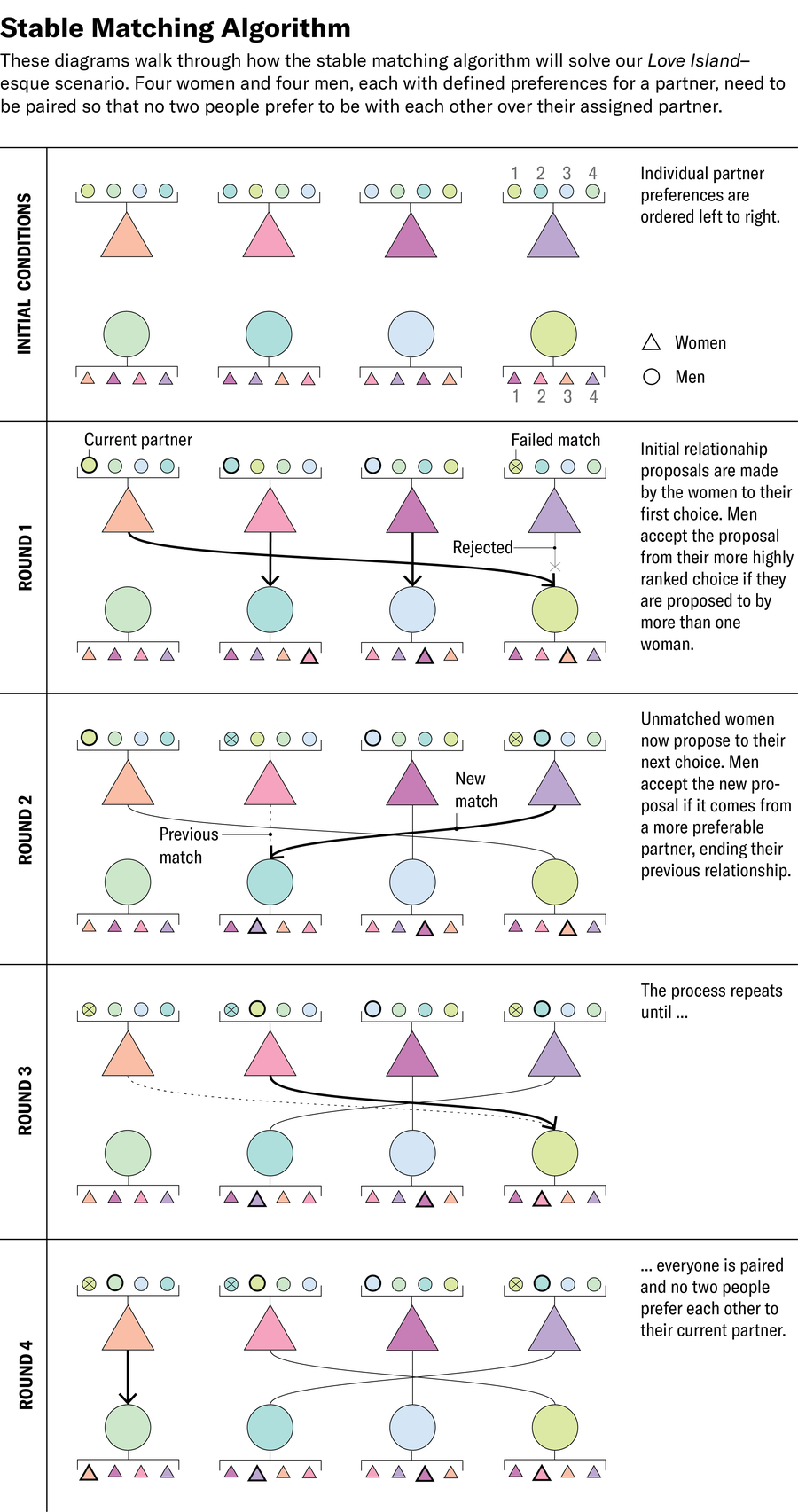
以下是它的工作原理。为了为我们的10位约会节目选手找到一组稳定、无戏剧性的合作伙伴关系,我们需要首先让每位选手按照偏好顺序对异性中的所有成员进行排名。
然后,在别墅的第一天,每位女性都向她首选的男性求爱。一些男性收到许多求爱,而另一些男性可能没有收到任何求爱。然后,每位男性都拒绝除他更喜欢的求爱者之外的所有人,从而为某些选手带来暂定的匹配,而另一些选手仍然未配对。
在第二天,每位被拒绝的女性都会向她的第二选择求爱(即使他已经配对)。男性会考虑新的求爱,如果他们更喜欢新的求爱者,则有些人可能会放弃当前的匹配。然后,一些新失恋的女性会向她们的下一个可能的伴侣求爱。
这个过程在第三天、第四天以及随后的几天重复进行,次数不限,直到每个人都确定了一个匹配对象。虽然并非每个人都会对使用此过程的配对感到满意,但从数学上可以保证,没有人会同时更喜欢与彼此在一起而不是他们目前的对象(假设他们的偏好在彼此了解后没有改变)。虽然这不能保证我们的爱之岛衍生剧仍然是一个轻松、无戏剧性的观看体验,但这可能已经是我们能得到的最好的结果了。
Zane Wolf
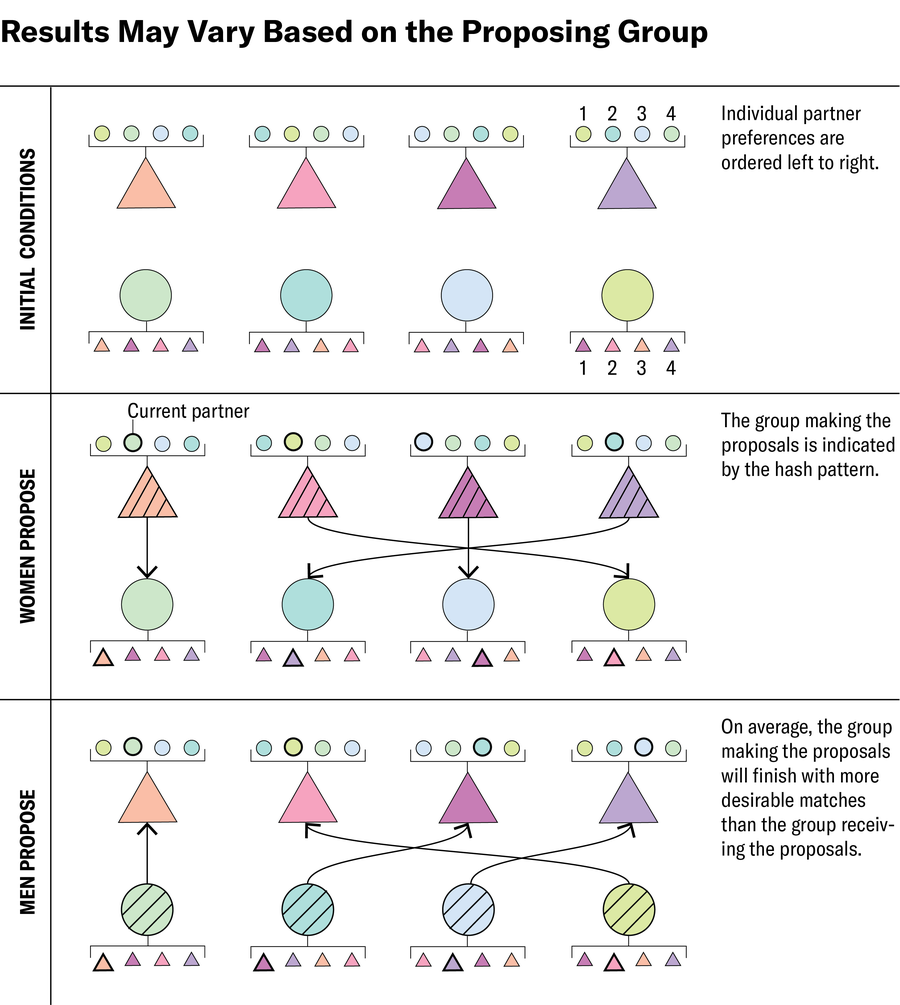
有趣的是,首先求爱的小组具有优势——当女性首先求爱时,平均而言,她们最终获得的匹配对象对她们而言比对男性而言更理想。“盖尔-沙普利算法的一个问题是,它会在任何一方给你带来这些极端的匹配,”加州大学欧文分校的计算机科学家维贾伊·瓦齐拉尼解释说。
结果可能略有失衡,但盖尔和沙普利的策略是无与伦比的。事实证明,自1950年代以来,一个组织一直在使用它的一个版本,该组织将医学生与全国各地的住院医师项目进行匹配。1984年,斯坦福大学经济学家阿尔文·罗斯使用盖尔和沙普利的数学语言表明,该组织使用的过程不仅保证了稳定的匹配,而且还是“策略证明”的——这意味着没有办法玩弄系统。这种特性,更普遍地称为激励相容性,之所以受到重视,是因为它意味着如果每个人都如实报告自己的偏好,他们最终都会获得最佳选择。
Zane Wolf
罗斯和经济学家埃利奥特·佩兰森也对该算法进行了一些调整。他们对其进行了调整,使其适用于已婚并希望在同一地点完成住院医师培训的医学生。他们还指出,住院医师处于劣势,因为医院先求爱。罗斯主张住院医师先求爱,以确保他们获得最佳结果。时至今日,医院和即将到来的住院医师都提供了彼此的排名,并且数学运算可以确保实现稳定状态。罗斯和沙普利因其工作获得了2012年诺贝尔经济学奖。
罗斯及其同事还使用这种数学语言来解决另一个棘手的匹配问题:将孩子分配到美国最大城市的公立学校。2003年,他们调整了盖尔-沙普利算法,将学生分配到纽约市竞争异常激烈的公立高中。在运营的第一年,与他们的首选之一相匹配的学生人数从大约50,000人增加到70,000多人。该算法的另一个版本也用于将学生分配到波士顿的公立学校。
回到浪漫领域,盖尔-沙普利算法甚至启发了Hinge等约会应用程序的内部运作。虽然用户没有明确地对他们的潜在匹配对象进行排名,但这些应用程序会观察用户的喜欢和不喜欢历史以及他们声明的约会偏好,以策划少量“最佳匹配对象”,并首先向用户展示。发送给潜在匹配对象的点赞或消息类似于原始算法中的“求爱”。
康奈尔大学计算机科学教授乔恩·克莱因伯格强调说:“像[盖尔-沙普利]这样的模型的威力在于将一个想法抽象到许多不同的设置中。”他表示,不同领域的“问题在概念上可以都有共同之处”,而盖尔-沙普利算法“为我们提供了一种数学语言来讨论[它们]。”
尽管该算法简单可靠,但如果排名中存在偏见,它也可能会放大现有的差距。《纽约城市报》是一家位于纽约市的非营利新闻机构,获得的数据显示,在许多顶尖学校,黑人和拉丁裔学生被大都市高中录取的比率通常低于白人和亚裔学生。住院医师匹配计划已被证明在种族和性别平等方面存在类似的缺陷。
波士顿学院经济学教授乌特库·云弗解释说:“真正的问题不是算法本身”,而是它们使用的排名数据以及它们部署的环境。这种动态在持续的人工智能繁荣中显而易见:随着复杂算法学会重现我们数据中的模式,它们通常也会复制我们的偏见。
康奈尔大学计算机科学教授艾娃·塔多斯说:“如果人类有偏见,那么我们的偏见就会在数据中。”研究人员已经提出了一些消除数据偏见的方法。例如,医院或学校等机构可以使用更大、更多样化的评审小组来对候选人进行排名。还可以使用其他算法来考虑已知的偏见,方法是在将排名用于匹配之前重新加权排名。
当然,没有算法可以保证婚姻或入学的幸福匹配。但最佳选择仍然是简单、透明且激励诚实的选项——因此,即使在60年后,似乎仍然没有比盖尔-沙普利算法更好的选择。
