乍一看,这个问题似乎荒谬地简单。然而,专家们徒劳地寻找解决方案数十年。据数学家杰弗里·拉加里亚斯说,数论学家角谷静夫告诉他,在冷战期间,“耶鲁大学大约有一个月的时间,每个人都在研究这个问题,但没有任何结果。当我在芝加哥大学提到这个问题时,也发生了类似的现象。有人开玩笑说,这个问题是减缓美国数学研究阴谋的一部分。”
考拉兹猜想——角谷静夫描述的这个令人烦恼的难题——是那些表面上简单但人们往往会迷失其中的问题之一。因此,经验丰富的教授经常警告他们雄心勃勃的学生不要沉迷于此,而忽略了他们实际的研究。
这个猜想本身可以很简单地表述出来,甚至小学生都能理解。取一个自然数。如果是奇数,乘以 3 再加 1;如果是偶数,除以 2。对结果x也以同样的方式进行:如果x是奇数,则计算 3x + 1;否则计算 x / 2。尽可能多地重复这些指令,根据猜想,你总是会得到数字 1。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
例如:如果你从 5 开始,你必须计算 5 x 3 + 1,结果是 16。因为 16 是一个偶数,你必须将它减半,得到 8。然后 8 / 2 = 4,除以 2 后得到 2——而 2 / 2 = 1。迭代计算的过程在五个步骤后将你带到终点。
当然,你也可以继续用 1 计算,得到 4,然后 2,然后再回到 1。计算规则将你带入一个无法逃脱的循环。因此,1 被视为过程的终点。

通过迭代计算,你可以从上面的任何数字开始,最终都会达到 1。
对不同的数字进行迭代计算规则并查看结果序列真的很有趣。如果你从 6 开始:6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1。或者 42:42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1。无论你从哪个数字开始,你似乎总是以 1 结尾。有些数字,例如 27,需要很长时间 (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...),但到目前为止,结果始终为 1。(诚然,你必须对起始数字 27 有耐心,它需要 111 步。)
但奇怪的是,仍然没有数学证明考拉兹猜想是正确的。这种缺失让数学家们困惑多年。
考拉兹猜想的起源尚不确定,这就是为什么这个假设有许多不同的名称。专家们谈到西拉古斯问题、乌拉姆问题、3n + 1 猜想、哈塞算法或角谷问题。
德国数学家洛塔尔·考拉兹在他的数学研究期间对迭代函数产生了兴趣并对其进行了研究。在 1930 年代初期,他还发表了关于该主题的专业文章,但以他的名字命名的问题的明确计算规则不在其中。在 1950 年代和 1960 年代,当数学家赫尔穆特·哈塞和角谷静夫等人将其传播到包括雪城大学在内的各个大学时,考拉兹猜想最终获得了 notoriety。
就像海妖的歌声一样,这个看似简单的猜想吸引了专家们。几十年来,他们一直在寻找证据,证明在重复考拉兹过程有限次数后,你最终会得到 1。这种坚持的原因不仅仅是问题的简单性:考拉兹猜想与其他重要的数学问题有关。例如,这种迭代函数出现在动力系统中,例如描述行星轨道的模型。该猜想还与黎曼猜想有关,黎曼猜想是数论中最古老的问题之一。
考拉兹猜想的经验证据
在 2019 年和 2020 年,研究人员在一个协作计算机科学项目中检查了 268 以下的所有数字,即序列中约 3 x 1020 个数字。该集合中的所有数字都满足作为初始值的考拉兹猜想。但这并不意味着某处没有异常值。可能存在一个起始值,在重复考拉兹过程后,产生越来越大的值,最终上升到无穷大。然而,如果从统计角度检查这个问题,这种情况似乎不太可能。
奇数n在迭代的第一步后增加到 3n + 1,但结果不可避免地是偶数,因此在下一步中减半。在所有情况的一半中,减半产生一个奇数,因此必须再次增加到 3n + 1,然后再次获得偶数结果。但是,如果第二步的结果再次为偶数,则在每四种情况中,你必须将新数字除以 2 两次。在每八种情况中,你必须将其除以 2 三次,依此类推。
为了评估数字序列的长期行为,拉加里亚斯在 1985 年根据这些考虑计算了几何平均值,并获得了以下结果:(3/2)1/2 x (3⁄4)1/4 x (3⁄8)1/8 · ... = 3⁄4。这表明序列元素在迭代计算规则的每个步骤中平均缩小 3⁄4 的因子。因此,起始值因该过程而增长到无穷大的可能性极低。
然而,可能存在一个起始值,它以一个不是 4 → 2 → 1 的循环结束。该循环可能包含更多的数字,以至于永远无法达到 1。
例如,如果你也允许考拉兹猜想使用负整数,则可以找到这种“非平凡”循环:在这种情况下,迭代计算规则不仅可以以 –2 → –1 → –2 → ... 结束,还可以以 –5 → –14 → –7 → –20 → –10 → –5 → ... 或 –17 → –50 → ... → –17 →.... 如果我们将自己限制为自然数,则迄今为止尚未知晓非平凡循环——但这并不意味着它们不存在。专家们现在已经能够证明,考拉兹问题中的这种循环必须由 至少 1860 亿个数字 组成。
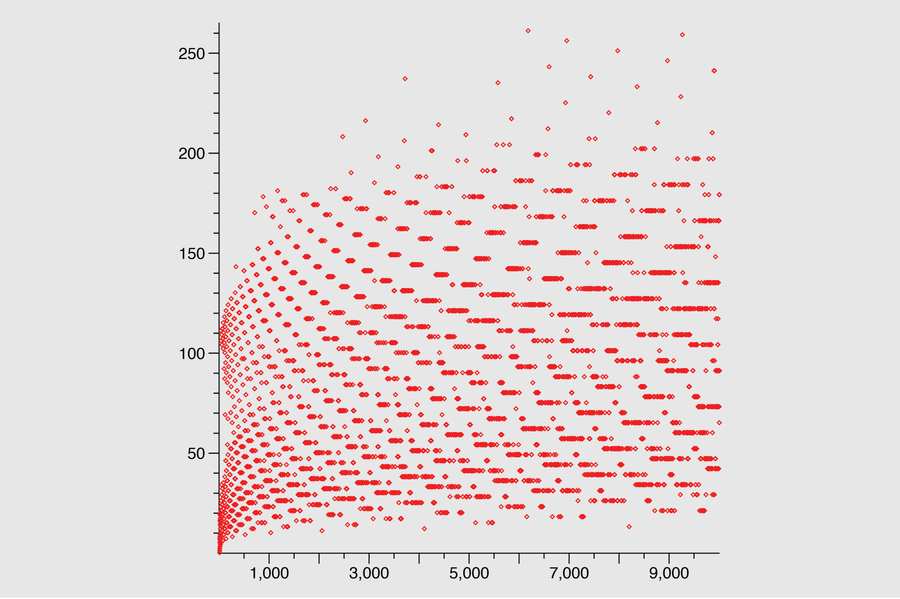
从 1 到 9,999 的所有数字的考拉兹序列的长度差异很大。
即使这听起来不太可能,但也并非不可能。在数学中,有很多例子表明,某些定律只有在考虑多次迭代后才会失效。例如,素数定理仅对大约 10316 个数字高估了素数的数量。在那之后,素数集合低估了素数的实际数量。
考拉兹猜想也可能发生类似的情况:也许在数轴深处隐藏着一个巨大的数字,它打破了迄今为止观察到的模式。
几乎所有数字的证明
几十年来,数学家们一直在寻找确凿的证据。2019 年,加州大学洛杉矶分校的菲尔兹奖获得者陶哲轩取得了最大的进展,当时他证明了几乎所有自然数的起始值最终都会以接近 1 的值结束。
“几乎所有”都有精确的数学含义:如果你随机选择一个自然数作为起始值,它有 100% 的概率以 1 结尾。(然而,零概率事件不一定是不可避免的事件。)陶哲轩在 2020 年的一次演讲中说,这“就像在没有实际解决考拉兹猜想的情况下尽可能接近它”。不幸的是,陶哲轩的方法无法推广到所有数字,因为它基于统计学考虑。
所有其他方法也都走入了死胡同。也许这意味着考拉兹猜想是错误的。“也许我们应该花更多的精力寻找反例,而不是我们目前所花的精力,”罗格斯大学数学家亚历克斯·孔托罗维奇在 Veritasium YouTube 频道上的一个视频中说。
也许考拉兹猜想将在未来几年内被确定为真或假。但还有另一种可能性:也许这确实是一个无法用现有数学工具证明的问题。事实上,在 1987 年,已故数学家 约翰·霍顿·康威 研究了 考拉兹猜想的推广并发现 迭代函数具有不可证明的属性。也许这也适用于考拉兹猜想。尽管它看起来很简单,但它可能注定永远无法解决。
本文最初发表于《Spektrum der Wissenschaft》,并经许可转载。
