1982 年的 SAT 考试臭名昭著地出现了一道数学题,这道题非常棘手,甚至连出题者都没有包含正确答案。这个错误导致 30 万份试卷需要重新评分,学生们成了这个棘手的硬币旋转悖论的受害者。
以下是这个悖论的原理:将两枚四分之一美元硬币平放在桌面上,使它们互相接触。按住其中一枚硬币使其静止在桌面上,滚动另一枚四分之一美元硬币绕着它转,保持两枚硬币边缘接触且不滑动。当移动的硬币回到其起始位置时,它已经完成了多少次完整旋转?换句话说,在下面的图中,乔治·华盛顿正面朝上的位置出现了多少次?如果你喜欢这样的谜题,花一分钟时间思考一下。
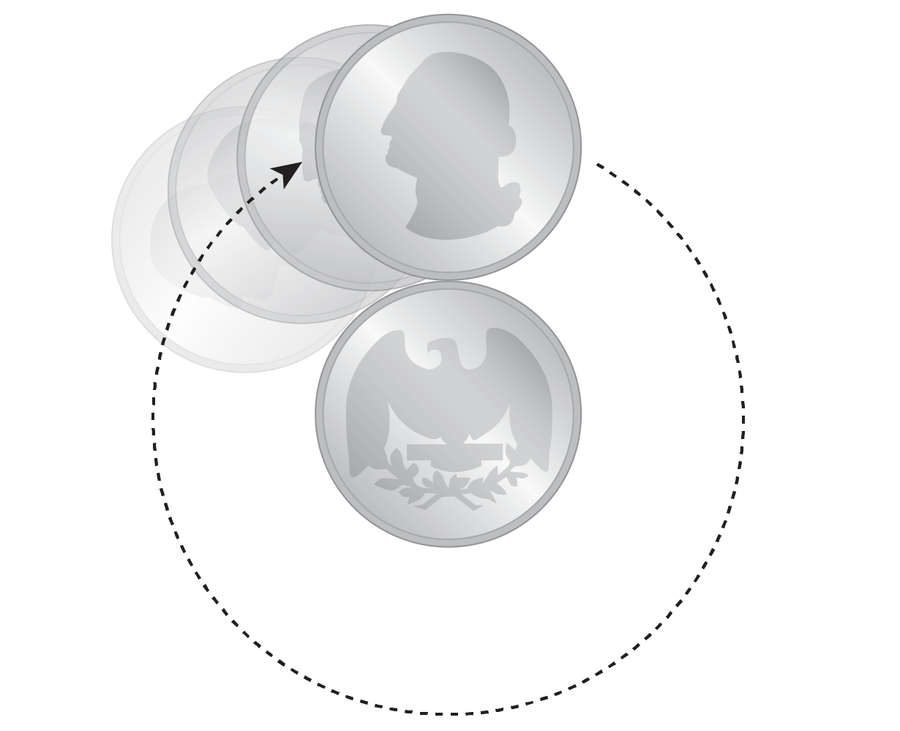
来源:阿曼达·蒙塔内斯
许多人认为乔治会完成一次完整旋转。一枚四分之一美元硬币的圆周长约为三英寸。因此,移动的硬币沿着一条长度为三英寸的路径滚动,这与它自身的圆周长相同。如果我们用一根绳子绕着一枚四分之一美元硬币,然后沿着三英寸的路径滚动它,同时展开绳子,那么肯定会展开三英寸长的绳子——刚好足够一次旋转。
事实上,移动的硬币在返回其原始位置时正好完成两次完整旋转。这种现象违背了常识。如果你觉得难以接受,我建议你亲自测试一下。任何两个大小相同的圆盘都可以。
[如需了解另一个数学探索,请阅读“‘睡美人问题’为何让数学家们彻夜难眠”]
1982 年SAT 数学部分中偷偷加入的这个问题的版本略有不同:中心圆盘比绕着它滚动的圆盘更大。以下是该问题的一个版本,措辞略有修改,使其更清晰:
圆 B 的半径是圆 A 半径的三倍。从图中所示位置开始,圆 A 绕圆 B 滚动。当圆 A 返回其起点时,它将完成多少次旋转?
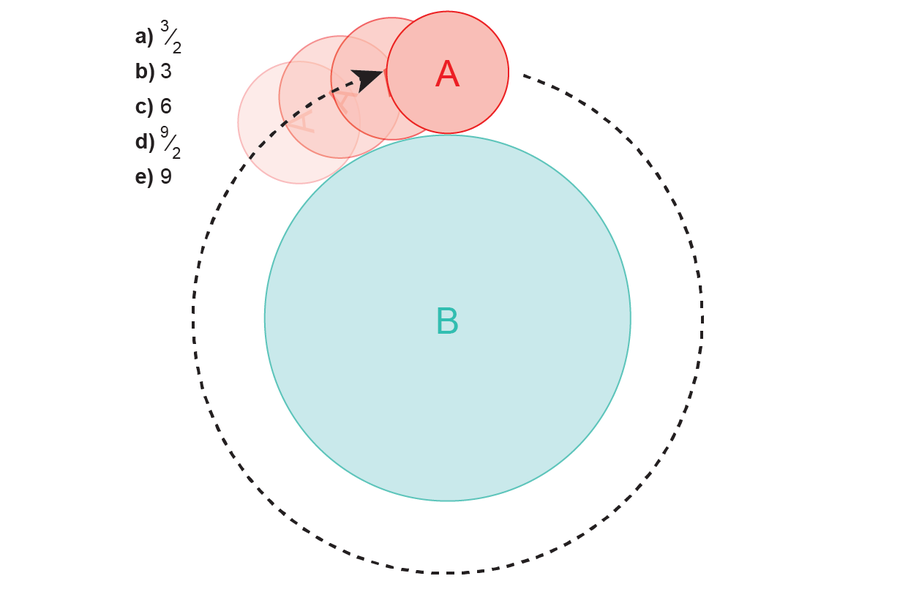
来源:阿曼达·蒙塔内斯
这看起来是否很熟悉?在这里,我们被告知较大圆的半径是较小圆半径的三倍。这意味着两个圆的圆周长也具有相同的比例:B 的周长是 A 的三倍。人们很容易推断出,较小的圆可以“展开”自身三次来包围较大的圆。因此,“3”是 SAT 考试中预期的多项选择答案。事实上,圆 A 在其行程中完成了四次旋转——同样,比直觉预期的多一次旋转。这个悖论远远超出了命题人的认知,以至于选项中没有提供“4”这个答案,因此即使是最聪明的学生也被迫提交了错误的答案。在参加包含该问题的考试的 30 万名学生中,有三名向大学理事会报告了这个问题,并且每份试卷都必须重新评分。
那么,为什么会多出一次旋转呢?上面导致我们误入歧途的方法确实包含一些道理。沿着三英寸直线路径滚动一枚四分之一美元硬币只会涉及一次旋转。同样,一个小圆在一个长度为其直径三倍的直线上滚动会旋转三次。因此,路径的圆形形状以某种方式引起了自身的旋转。为了理解原因,想象一下绕着一颗微小的罂粟种子滚动一枚四分之一美元硬币。即使绕种子的长度可以忽略不计,乔治也会旋转一次。因此,旋转有两个来源:一个来自沿着路径滚动(路径越长,旋转次数越多),另一个来自绕物体旋转,无论物体大小如何,它都会贡献一次旋转。
另一个有用的视角来自想象绕着正方形滚动一枚四分之一美元硬币。正方形的每条边都是直线段,乔治的头像每三英寸长度会旋转一次,但是当你到达一个角时,四分之一美元硬币将不得不旋转更多才能通过那个角。(同样,如果难以想象,请亲自尝试一下。)事实证明,角落处的额外旋转正好是 90 度,这导致当硬币穿过正方形的所有四个角并返回起点时,总共旋转了一整圈(360 度)。类似地,绕着三角形滚动将需要在每个角处旋转 120 度。
这种效应可以放大到天体。众所周知,月球有远端,并且总是将同一面朝向我们地球人。许多人错误地认为,月球不变的面貌意味着它一定不像地球那样绕其轴自转。但是,如果月球在绕轨道运行时不自转,那么我们会从地球上的某些地方看到它的远端。你可以用自己的拳头来演示这一点——保持一个拳头静止,然后让另一个拳头绕着它旋转,而没有任何自转。站在你静止的指关节上的人会看到不同时间 orbiting 拳头的不同景象。为了永远隐藏其背面,月球必须在完成一次轨道运行时旋转一次。(轨道时间和自转时间之间的这种完美一致性并非天文巧合,而是一个称为潮汐锁定现象的例子。我们也在回避我们的相对论参考系,向阿尔伯特·爱因斯坦致歉。)对于硬币和 SAT 问题,我们看到旋转有两个来源:一些来自沿着任何路径的“直线”滚动,另一个来自绕物体旋转的额外旋转。月球不做任何直线滚动。如果地球是平的,月球将在其上方滑行而不会滚动。因此,月球的单次旋转完全是因为它围绕非常球形的地球公转。
如果你有一个太阳系的鸟瞰图,你会在典型的一年中看到地球完成多少次旋转?许多人会说是 365 次,但再一次,他们的答案会比正确答案少一次:366 次。(请注意,这与闰年无关,闰年是完全不同的事情。)人类将一天定义为太阳返回到天空同一位置所需的时间。总是让太阳在中午正上方是很方便的。但是,当地球完成一次旋转时,太阳实际上还没有完全回到天空中的位置。让我们重新审视 SAT 图表,看看发生了什么——这次我们将在小圆上标记一个固定点,并观察当小圆绕大圆滚动时该点会发生什么变化:
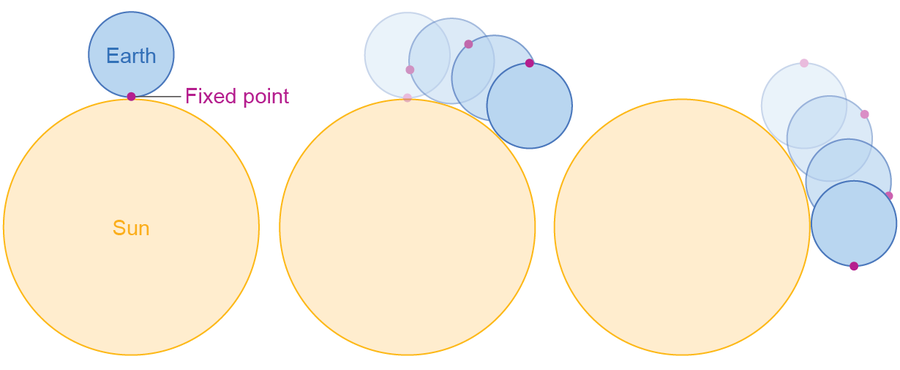
来源:阿曼达·蒙塔内斯
将大圆想象成太阳,小圆想象成地球(未按比例),点想象成我们星球上的一个固定点。在第一张图中,点直接盯着太阳。现在正好是中午。在最后一张图中,小圆完成了一次完整旋转(点再次指向下方),但请注意,对于站在该点的人来说,现在不是中午。小圆需要向前移动一点点超过一次旋转,才能使该点再次亲吻大圆。同样,尽管地球在 23 小时 56 分钟内完成一次旋转(这被称为恒星日),但太阳需要多花四分钟才能返回到天空中的正上方位置,从而产生我们定义的 24 小时制的一天。在 365 天的过程中,每天多出的这四分钟旋转加起来就是额外的一次旋转。
感谢您与我们一起滚动浏览硬币、测试错误和行星运动之旅——这足以让任何人头晕目眩。
编者注(2023 年 6 月 24 日):这篇文章在发布后经过编辑,将“月球的阴暗面”的说法更改为“月球的远端”。
