黎曼猜想是数论中最重要的未解问题——如果不是整个数学界的话。它已经困扰专家们超过160年。这个问题既出现在数学家大卫·希尔伯特1900年的开创性演讲中,也出现在一个世纪后提出的“千禧年难题”中。解决这个问题的人将赢得一百万美元的奖金。
但是,黎曼猜想是一块难啃的骨头。尽管付出了数十年的努力,众多专家的兴趣和现金奖励,但进展甚微。现在,麻省理工学院的数学家拉里·格思和牛津大学的詹姆斯·梅纳德在预印本服务器arXiv.org上发布了一项轰动性的新发现。德国波恩大学的数论学家瓦伦丁·布洛默说,在这篇论文中,“作者改进了一个看似50多年来无法逾越的结果。”
其他专家也同意。数学家和菲尔兹奖得主陶哲轩在Mastodon上写道,这项工作是“一个了不起的突破”,“尽管距离完全解决这个猜想还很遥远。”
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
黎曼猜想关系到自然数的基本组成部分:质数,即大于1且只能被1和自身整除的值。例如,2、3、5、7、11、13等等。*
每个其他数字,例如15,都可以清楚地分解为质数的乘积:15 = 3 x 5。问题是质数似乎没有遵循简单的模式,而是随机地出现在自然数中。十九世纪德国数学家伯恩哈德·黎曼提出了一种处理这种特性的方法,解释了质数如何在数轴上分布——至少从统计学的角度来看。
数字的元素周期表
证明这个猜想将为数学家提供不亚于一种“数字的元素周期表”的东西。正如物质的基本组成部分(如夸克、电子和光子)帮助我们理解宇宙和我们的世界一样,质数也发挥着重要的作用,不仅在数论中,而且在几乎所有数学领域中。
现在有许多定理是基于黎曼猜想的。证明这个猜想也将证明许多其他定理——这是解决这个顽固问题的又一个动力。
对质数的兴趣可以追溯到数千年前。早在公元前300年,欧几里得就证明了质数的数量是无限的。尽管人们对质数的兴趣持续存在,但直到18世纪,关于这些基本组成部分才取得任何进一步的重大发现。
作为一名15岁的少年,物理学家卡尔·弗里德里希·高斯意识到,质数的数量沿着数轴递减。他所谓的质数定理(直到100年后才被证明)指出,在从0到n的区间内,大约出现n/ln(n)个质数。换句话说,质数定理为数学家提供了一种估计质数在数轴上的典型分布的方法。
然而,质数的精确数量可能与定理给出的估计值不同。例如:根据质数定理,在1到100之间的区间内,大约有100/ln(100) ≈ 22个质数。但实际上有25个。因此,存在3的偏差。这就是黎曼猜想的用武之地。这个猜想为数学家提供了一种估计偏差的方法。更具体地说,它指出这种偏差不会变得任意大,而必须最多与n的平方根成比例,n是所考虑区间的长度。
因此,黎曼猜想并没有准确预测质数位于何处,而是假定它们在数轴上的出现遵循一定的规则。根据黎曼猜想,质数的密度根据质数定理而降低,并且质数根据这个密度均匀分布。这意味着没有大片区域完全没有质数,而另一些区域则充满了质数。
您也可以通过思考房间空气中分子的分布来想象这个想法:地板上的总体密度略高于天花板,但粒子——遵循这种密度分布——仍然均匀分散,并且任何地方都没有真空。
一个奇怪的联系
黎曼在1859年以一篇简短的六页出版物(他唯一对数论领域的贡献)中提出了以他名字命名的猜想。然而,乍一看,他的工作与质数几乎没有关系。
他处理了一个特定的函数,即所谓的zeta函数ζ(s),这是一个无限长的和,它将自然数的倒数值加起来,这些自然数被提高到s的幂

甚至在黎曼的工作之前,专家们就知道这样的zeta函数与质数有关。因此,zeta函数也可以表示为所有质数p的函数,如下所示
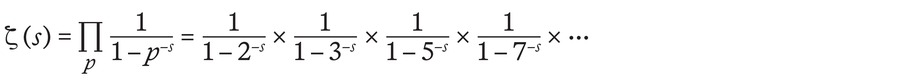
当黎曼不仅使用s的实数值,而且还使用复数时,他认识到这种与质数联系的全部意义。这些数字包含实部和负数的根,即所谓的虚部。
您可以将复数想象成一个二维结构。它们不是在数轴上标记一个点,而是位于平面上。x坐标对应于实部,y坐标对应于虚部
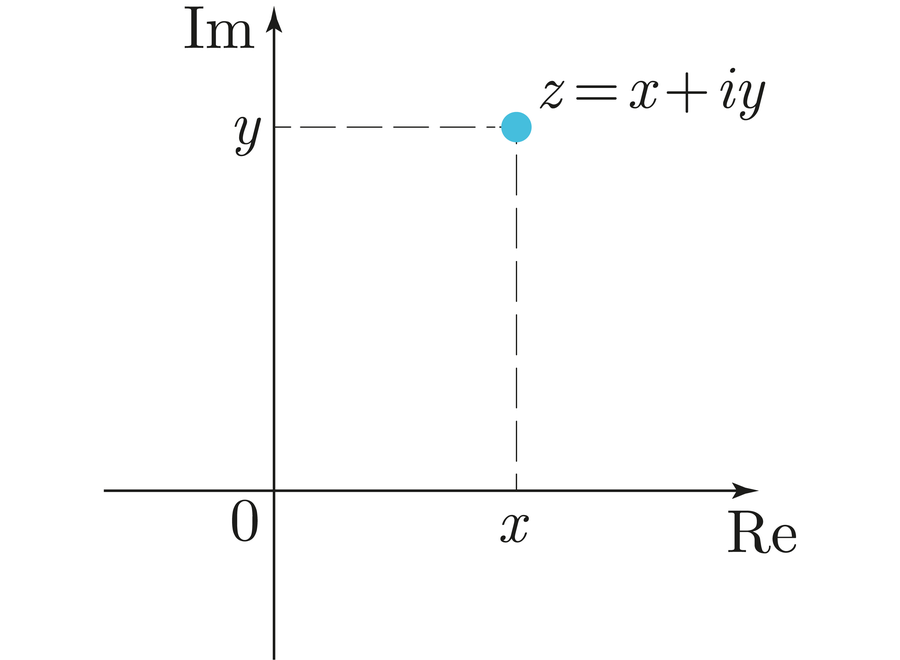
Никита Воробьев/Wikimedia
黎曼研究的复zeta函数可以可视化为平面上方的景观。事实证明,在群山和山谷之间,有一些点在质数关系中起着重要作用。这些点是zeta函数变为零的点(所谓的零点),景观降至海平面,可以这么说。
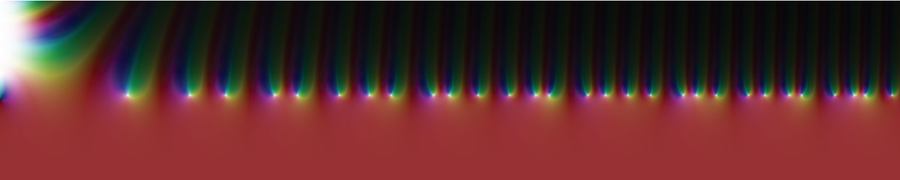
颜色代表复zeta函数的值,白色点表示其零点。
Jan Homann/Wikimedia
黎曼很快发现,如果实部大于1,则zeta函数没有零点。这意味着直线x = 1右侧的景观区域永远不会降至海平面。zeta函数的零点对于实部的负值也是已知的。它们位于实轴上,x = –2、–4、–6等等。但是,真正让黎曼以及此后所有数学家感兴趣的是“临界带”0 ≤ x ≤ 1中zeta函数的零点。
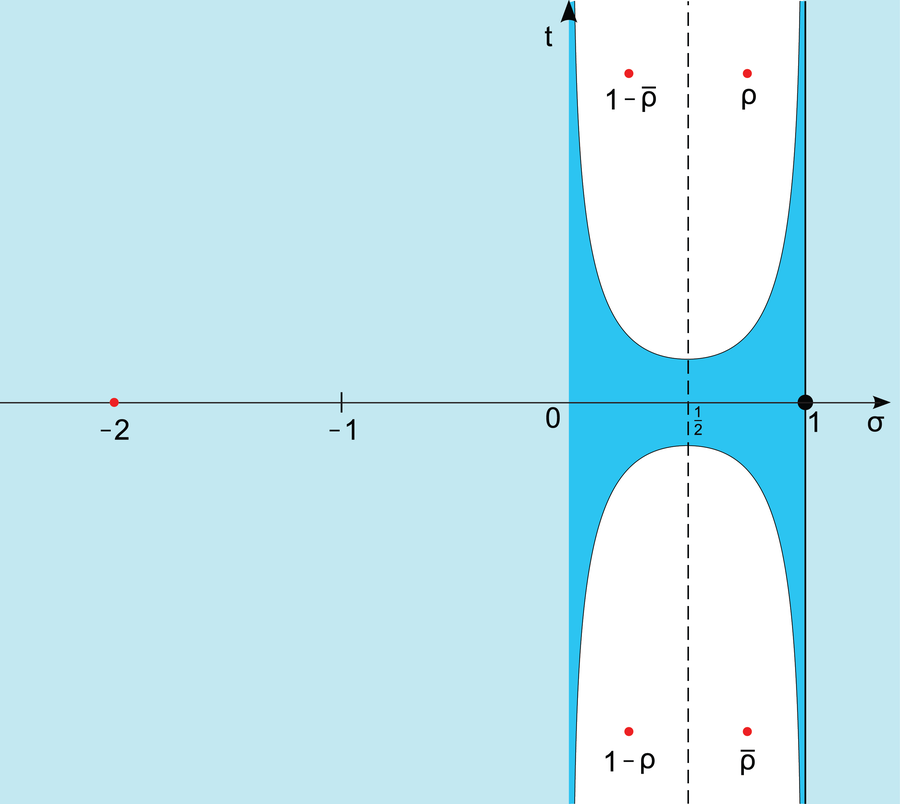
在临界带(深蓝色)中,黎曼zeta函数可能具有“非平凡”零点。黎曼猜想指出,这些零点仅位于直线 x = 1/2(虚线)上。
LoStrangolatore/Wikimedia (CC BY-SA 3.0)
黎曼知道zeta函数在临界带内有无限个零点。但有趣的是,所有零点似乎都位于直线x = 1/2上。因此,黎曼假设临界带内zeta函数的所有零点的实部都为x = 1/2。这个陈述实际上是理解质数分布的关键。如果正确,那么质数在数轴上的位置永远不会与质数集偏差太大。
寻找零点
迄今为止,数十亿甚至数百亿个zeta函数零点已经被检查过——超过1013个——并且全部都位于直线x = 1/2上。
但仅凭这一点还不是有效的证明。您只需要找到一个偏离此方案的零点即可证伪黎曼猜想。因此,我们正在寻找一个证明,明确表明在临界带中,x = 1/2之外没有零点。
到目前为止,这样的证明仍然遥不可及,因此研究人员采取了不同的方法。他们试图证明,在直线x = 1/2之外,最多只有一定数量N的零点。希望是将N减少到某个点N = 0,从而证明黎曼猜想。不幸的是,这条路径也被证明极其困难。1940年,数学家阿尔伯特·英厄姆能够证明,在0.75 ≤ x ≤ 1之间,最多有y3/5+c个零点,其虚部最多为y,其中c是0到9之间的常数。
在随后的80年中,这种估计几乎没有改进。上一次值得注意的进展来自数学家马丁·赫胥黎,在1972年。“这限制了我们在解析数论中做很多事情,”陶哲轩在他的社交媒体帖子中写道。例如,如果您想将质数定理应用于[x, x + xθ]类型的短区间,您会被英厄姆的估计限制在 θ > 1/6。
然而,如果黎曼猜想是正确的,那么质数定理适用于任何区间(或 θ = 0),无论区间有多小(因为 [x, x + xθ] = [x, x + 1] 适用于 θ = 0)。
现在,在2022年被授予著名菲尔兹奖的梅纳德和格思成功地首次显著改进了英厄姆的估计。根据他们的工作,在0.75 ≤ x ≤ 1范围内,zeta函数最多有y(13/25)+c个零点,其虚部最多为y。这到底意味着什么?布洛默解释说:“作者在定量意义上表明,黎曼zeta函数的零点离临界直线越远就越稀有。换句话说,对黎曼猜想的可能违反情况越糟糕,它们就越少发生。”
陶哲轩写道:“这传播到解析数论中的许多相应改进。” 这使得可以缩小质数定理适用的区间的尺寸。该定理适用于[x, x + x2/15],因此 θ > 1/6 = 0.166... 变为 θ > 2⁄15 = 0.133...
为了取得这一进展,梅纳德和格思最初为他们的结果使用了傅里叶分析中的众所周知的方法。这些技术类似于将声音分解为其泛音的技术。“最初的几个步骤是标准的,许多解析数论学家,包括我自己,都曾尝试突破英厄姆界限,都会认出它们,”陶哲轩解释说。然而,从那里开始,梅纳德和格思“做了一些聪明且出乎意料的操作,”陶哲轩写道。
布洛默表示赞同。“这项工作提供了一整套新的想法,正如作者正确指出的那样,这些想法可能可以应用于其他问题。从研究的角度来看,这是这项工作最决定性的贡献,”他说。
因此,即使梅纳德和格思尚未解决黎曼猜想,他们至少为解决这个有160年历史的难题提供了新的思路。谁知道呢——也许他们的努力掌握着最终破解这个猜想的关键。
本文最初发表于Spektrum der Wissenschaft,并经许可转载。
*编者注(2024年7月9日):这句话在发布后进行了编辑,以更好地澄清质数不包括1。
