啤酒冰镇后饮用最佳,事实证明,数学可以对此有所帮助。巴西圣若昂-德尔-雷联邦大学的克劳迪奥·德·卡斯特罗·佩莱格里尼最近着手制定一个方程式,以确定啤酒杯的最佳形状,从而使饮料保持美味的冰镇状态——换句话说,他正在寻找一种可以防止杯中液体吸收热量的玻璃杯。
最简单的方法是找到一个表面积相对于其体积尽可能小的容器。这是因为来自玻璃杯周围环境的热量会渗透到玻璃杯的表面。表面越小,进入的热量就越少,啤酒保持令人愉悦的凉爽的时间就越长。早在古代,学者们就认识到,在二维情况下,圆形提供了周长与面积的最小比率。这一发现也适用于三维:与体积相比,球体的表面积最小。
但是球形啤酒杯会很不方便。更重要的是,佩莱格里尼对静态情况不感兴趣,在静态情况下,你将啤酒放在玻璃杯中,然后看着液体变暖。“这个过程非常简单:点一杯啤酒,服务员送来,上酒,饮用。重复。”他在描述这项研究的预印本论文中写道,该论文于 10 月份发布到 arXiv.org 服务器。这意味着玻璃杯内的液位会发生变化,与环境接触的表面也会发生变化。(随着玻璃杯中的啤酒被喝掉更多,其更多的表面会接触到周围的空气。)
支持科学新闻事业
如果您喜欢这篇文章,请考虑支持我们屡获殊荣的新闻事业,方式是 订阅。通过购买订阅,您将有助于确保未来能够继续报道有关塑造我们当今世界的发现和思想的具有影响力的故事。
佩莱格里尼从玻璃杯形状的一些约束条件开始。它应该由一个绝缘的平底座组成,底座要足够大,以使玻璃杯能够直立。此外,玻璃杯应该是对称的,因此其形状由旋转体表示,即通过将二维形状绕 x 轴或 y 轴旋转 360 度而创建的三维形状。为了确定最佳啤酒杯形状,佩莱格里尼调整了定义旋转体的二维形状。在 2 月份 arXiv.org 上详细介绍的早期预印本分析中,他以这种方式描述了最佳玻璃杯形状,但最可行的容器体积超过两升,而最大的玻璃杯体积超过 100 升。
接下来,佩莱格里尼旨在设计一个实用的啤酒杯。但他必须做一些简化。他假设底座可以完美地隔热。(实际上,厚玻璃底座和杯垫的使用有所帮助,但完美的绝缘是不可能的。)他还假设啤酒的温度在液体中处处相同,并且饮料具有均匀的密度,这对于过滤后的品种来说基本上是正确的。佩莱格里尼忽略了啤酒泡沫作为可能的绝缘层。最后,他还忽略了人手向玻璃杯的热传递,仅研究了环境温度的影响。“在最关键的情况下,例如在 [38 摄氏度] 的海滩上刮风的日子里,只需 3 分钟就可能足以(再次基于个人经验,反复验证)使啤酒变得无法饮用,”佩莱格里尼写道。
最佳啤酒杯的公式
基于这些假设,研究人员创建了一个方程,描述了啤酒温度随时间的变化。这是一个微分方程,意味着该公式包含一个导数:一个函数,显示了变化率(在本例中为温度)相对于变量的变化率,在这种情况下,变量是啤酒杯的形状

这里,T 是啤酒温度,TU 是环境温度,cp 是比热容(物质升温的难易程度),ρ 是密度,V 是体积,Atot 是啤酒的暴露表面(包括侧面和上部圆形表面),hCV 是对流换热系数,表示其导热能力。使用这个公式,佩莱格里尼计算出了四个确保啤酒尽可能缓慢降温的技巧。
最好的情况是,您应该在凉爽的地方享用啤酒,以便 TU 尽可能低。
如果您使用陶瓷等更具绝缘性的材料代替玻璃,则导热系数会降低。
总的来说,佩莱格里尼指出,厚厚的泡沫层可以隔离啤酒,并防止二氧化碳过快流失。此外,应避免风和气流,因为这些会导致强制对流,与此处考虑的自然对流相比,强制对流在热传递中起着更大的作用。
所有这些技巧通常只能通过移动到不同的位置来遵循。如果您舒适地坐在酒吧里,您将暴露于当地的条件,因此,如果酒吧从一开始就使用形状经过优化的玻璃杯以实现最小的热交换,那将是非常受欢迎的。剧透:情况并非如此。
啤酒香槟杯
啤酒杯的形状包含在上述方程中的商 Atot⁄V 中。该数字越小,温度变化就越小。这就是佩莱格里尼专注于最小化 Atot⁄V 值的原因。
在学校里,数学家们了解到,这种优化任务可以通过导数来解决。例如,要找到抛物线 f(x) = x2 + 3x + 2 的顶点,该函数是从 x 导出的,结果设置为零:0 = 2x + 3。这意味着顶点可以在 x = –1.5 处找到。
佩莱格里尼以完全相同的方式进行:他导出了商 Atot/V,将其设置为零,然后使用旋转体的属性推导出了最佳啤酒杯形状的函数。根据这个,完美啤酒杯的半径 r 作为高度 h 的函数,由以下公式给出

C 是一个常数,Rb 是玻璃杯底座的半径。该公式表明,玻璃杯的杯口应该很大,并且玻璃杯应该向底部变窄,类似于许多常见的啤酒杯。然而,现实世界中玻璃杯的半径并非总是逐渐变小——它们通常具有弯曲的 S 形,从侧面看是这样。这使它们与完美的啤酒杯区分开来。
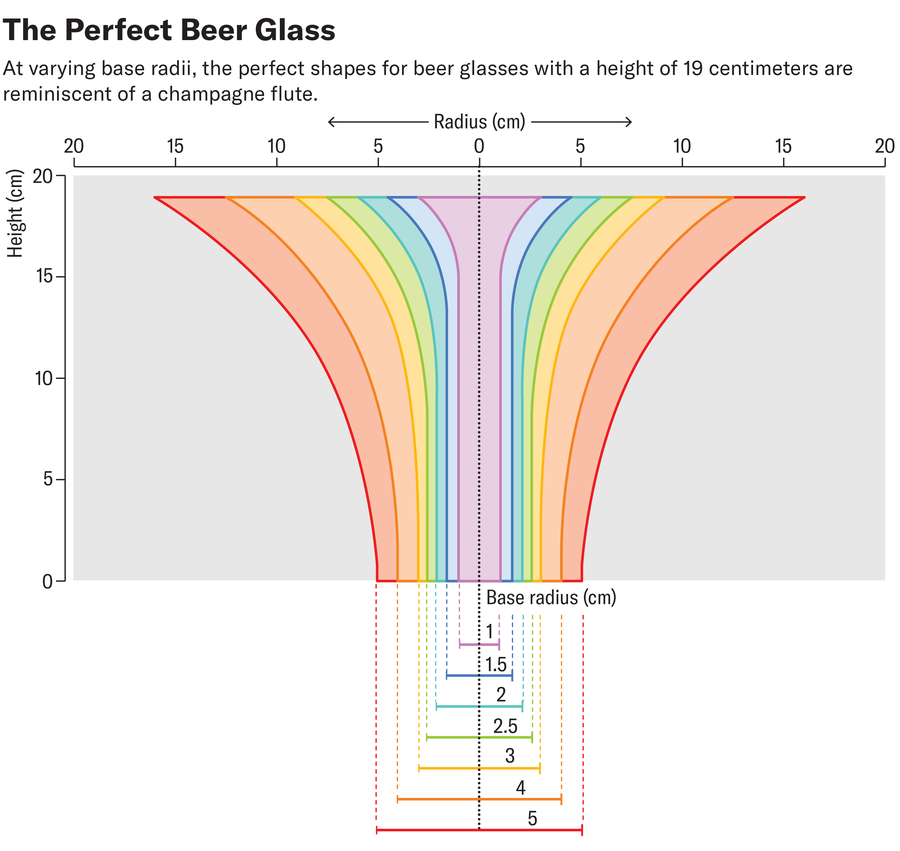
克劳迪奥·德·卡斯特罗·佩莱格里尼,由阿曼达·蒙塔涅斯修改和重新设计;来源:克劳迪奥·C·佩莱格里尼的“优化啤酒杯形状以最大限度地减少热传递——新结果”。预印本于 2024 年 10 月 15 日发布至 https://arxiv.org/abs/2410.12043
最佳玻璃杯的确切形状取决于玻璃杯底座的半径和常数 C,常数 C 由玻璃杯的高度等因素决定。佩莱格里尼首先计算了高度为 19 厘米的不同底座半径的玻璃杯的最佳形状。由此产生的形状让人联想到香槟杯。
然后,工程师调整了完美玻璃杯的参数,以适应不同类型的啤酒杯,例如英制品脱杯、美式品脱杯或小麦啤酒杯,这些啤酒杯在英国广泛使用。为此,佩莱格里尼将相应的底座半径和高度输入到他的公式中,以计算最佳形状。
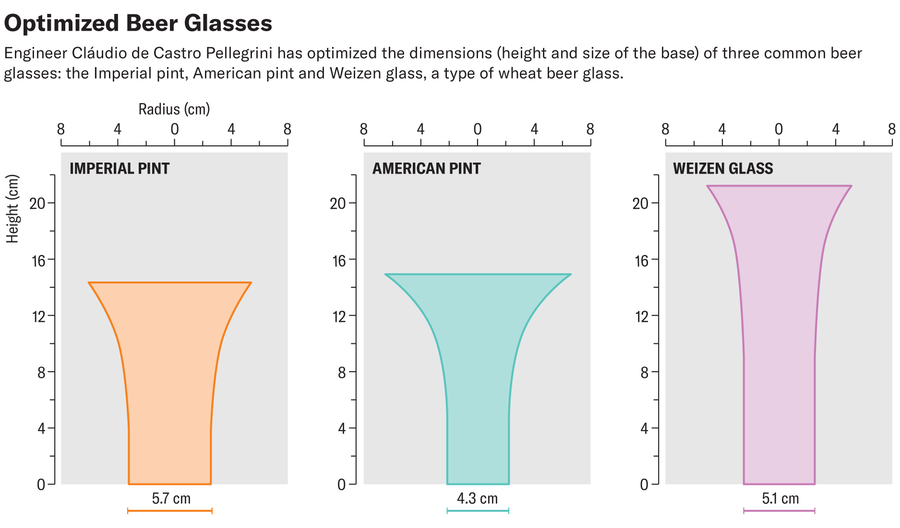
克劳迪奥·德·卡斯特罗·佩莱格里尼,由阿曼达·蒙塔涅斯修改和重新设计;来源:克劳迪奥·C·佩莱格里尼的“优化啤酒杯形状以最大限度地减少热传递——新结果”。预印本于 2024 年 10 月 15 日发布至 https://arxiv.org/abs/2410.12043
在这里,对于所有类型,大致形状看起来也相同,并且让人联想到香槟杯。但即使是非最佳玻璃杯也有一些好处,佩莱格里尼在预印本中写道。虽然在巴西广泛使用的 Nadir Figueiredo 玻璃杯远非最佳形状,但它们在某些方面仍然是为热传递而完美设计的:因为它们容纳的啤酒量相对较小,人们通常会比啤酒明显变暖之前更快地喝完啤酒。
本文最初发表于《明镜》周刊,并经许可转载。
